Since the development of micro-electro-mechanical systems (MEMS) accelerometers, people have been committed to the miniaturization, intelligence, and integration of MEMS accelerometers [1]. Accelerometers can be classified as capacitive, piezoresistive, piezoelectric, resonant, or tunneling according to the different sensitivity modes [2]. Among these, capacitive accelerometers have seen significant development due to their good stability, high detection accuracy, and good process compatibility. In the development of biaxial accelerometers, cross-coupling between orthogonal sensitive axes has been a major concern, as cross-coupling errors often lead to output deviations in accelerometers [3], [4], originating from various aspects of biaxial accelerometers.
MEMS accelerometers have evolved from single-axis to dual-axis architectures [5]. Through innovative technologies such as cross-shaped support structures and decoupled spring systems, two mutually perpendicular sensing axes are integrated into a single-chip structure [6], [7], [8], significantly reducing device size while maintaining a cross-axis suppression ratio better than −40 dB [9]. The most advanced designs now use advanced materials such as graphene-silicon heterostructures [10] and three-dimensional silicon vias [11] to achieve a noise density as low as 0.3 mg/√Hz. These advancements have made dual-axis accelerometers indispensable for scenarios requiring synchronized multi-directional measurement.
Despite these achievements, the performance of dual-axis MEMS accelerometers degrades significantly under temperature variations, posing a fundamental limitation for deployment in environments with wide thermal swings [12]. The root causes of temperature instability are multifaceted. At the mechanical level, temperature variations cause non-uniform thermal expansion of the silicon-based sensitive structure, altering the capacitance gap between the mass block and the fixed electrode, as well as the stiffness of the elastic beam, directly affecting detection sensitivity [13]. At the system level, the symmetry of the dual-axis structure is disrupted due to of thermal stress mismatch, resulting in cross-axis sensitivity temperature drift and causing the output at the same point to be non-reproducible [14].
The current compensation strategy addresses these challenges through both passive and active approaches. Passive methods focus on material selection and symmetrical mechanical design [15], [16], while active technologies employ additional temperature sensors and algorithmic corrections [17], [18], [19], [20]. However, passive methods often fail to meet requirements over a wider temperature range, while active methods increase system complexity and power consumption. This work introduces a dual-axis MEMS accelerometer design that combines a hybrid nested sensing mechanism with a differential compensation architecture. Through passive design, it achieves offset drift of less than 1.26 mg/°C and 0.91 mg/°C in the two axes throughout the range from −40 °C to 60 °C. After the algorithm correction was added, the bias drift of the biaxial accelerometer over the full temperature range was less than 0.05 mg/°C, which was increased five times. The following section introduces the mechanical design principles of the nested dual-axis accelerometer, followed by the implementation and verification of the compensation system.
The coupling error between orthogonally sensitive axes is one of the most important design parameters of biaxial accelerometers and must be carefully considered during the accelerometer design stage. To reduce the inter-axis coupling error of biaxial MEMS accelerometers caused by machining and assembly errors, this paper proposes a nested biaxial accelerometer that achieves smaller size, higher structural utilization and lower inter-axis coupling error.
The nested biaxial accelerometer consists of two frames (Fig. 1). The outer frame is the X-axis sensitive detection frame, and the inner frame is the Y-axis sensitive detection frame. The sensitive masses of the outer and inner frames are connected to their respective anchors via folded beams, with no rigid connection between them.
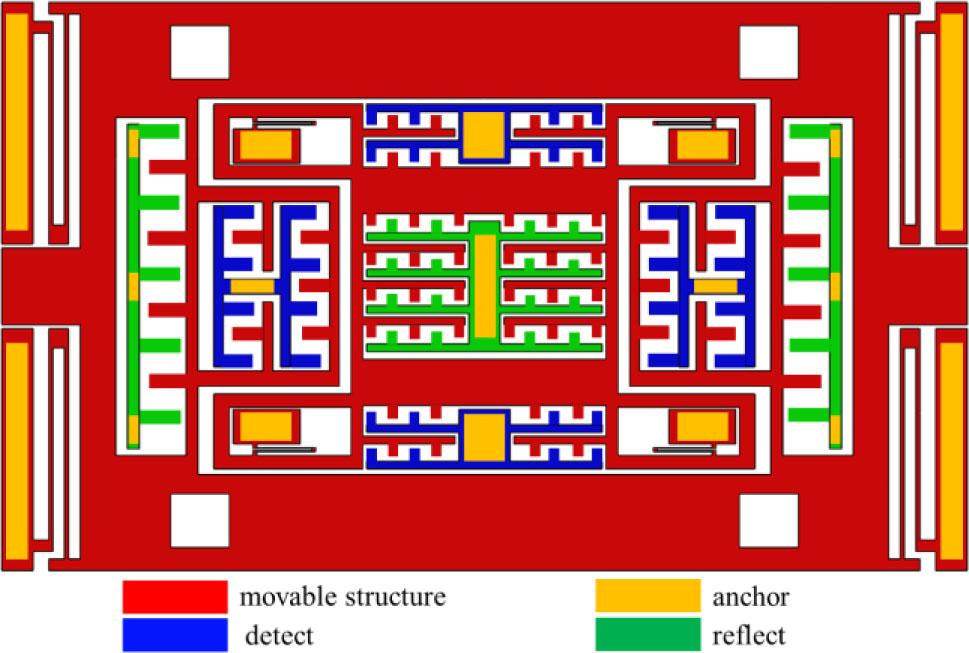
Biaxial accelerometer model.
The sensitive masses of the outer and inner frames differ, as do the size and stiffness of their folded beams. This ensures that when an acceleration signal is input, the sensitive axial structures are not affected by the orthogonal axial masses, achieving structural decoupling and reducing inter-axis coupling.
Folded beams are used as elastic connecting beams for both frames, as they have high stiffness in the orthogonal direction of the sensitive axis and are less affected by orthogonal acceleration. Differential sliding film detection combs are used to eliminate capacitance variations in orthogonal and sensitive directions. Closed-loop control is employed to improve device stability and reduce coupling caused by vibration.
The structure motion equation is given in (1), where mx and my are the two different sensitive masses; kx, ky, cx, and cy are the equivalent stiffness and damping of the two detection axes; and x, and y are the displacements along the sensitive axes, respectively. The matrices on the left side of the equation represent the inertial force, damping force, elastic force, and static force of the sensitive mass, respectively. Their sum is equal to the driving force generated by the external acceleration, shown on the right side of the equation.
Expanding (1) yields the kinetic equations for this accelerometer when detecting a closed loop.
Fig. 2 shows the operational modes of the accelerometer along its two sensitive axes. This modal separation design prevents cross-axis coupling and interference.
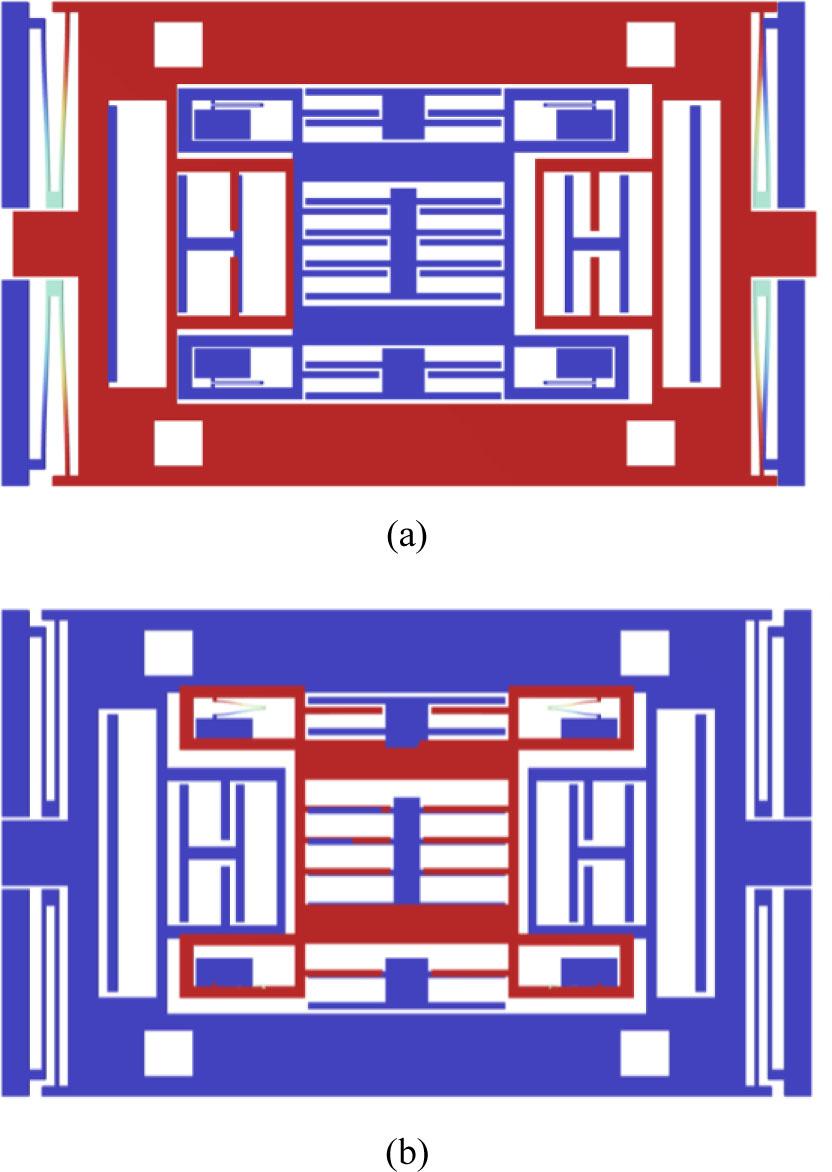
The two effective modes of the biaxial accelerometer: (a) X-axis working mode, frequency is 4149 Hz; (b) Y-axis working mode, frequency is 7454 Hz.
The framework of the closed-loop control system and temperature compensation system for the accelerometer is shown in Fig. 3. The core of this temperature compensation system is to dynamically correct mechanical and circuit errors caused by temperature through closed-loop control. The acquisition module synchronously acquires the X/Y-axis output signals of the accelerometer, data from the temperature sensor, and the closed-loop feedback voltage, then converts them into digital signals through the ADC. The compensation algorithm calculates the zero-g offset and scale factor temperature coefficient (TC) in real time based on the preset temperature model, and injects the correction parameters into the closed-loop control system. Dynamic error compensation is achieved by adjusting the input code value of the feedback DAC or the gain of the C/V converter. The control circuit uses a standard closed-loop architecture, with a key modification: integrating a temperature sensor (PT1000) into the feedback loop for real-time adjustment.
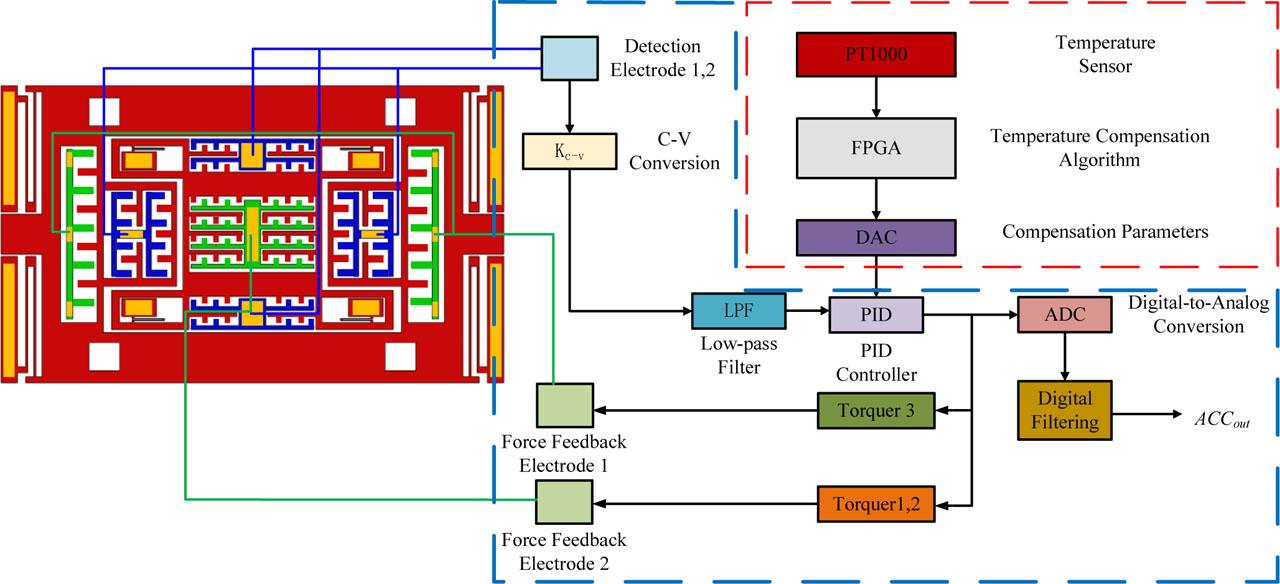
Closed-loop control and temperature compensation system block diagram.
Unlike traditional closed-loop circuits, this design integrates a real-time temperature-sensing module (PT1000) directly with the C/V converter, enabling simultaneous adjustment of feedback voltage and gain based on temperature, which reduces latency by 30 % compared to existing architectures [17].
In this temperature compensation system, a second-order polynomial model is used for fitting, and its expression is:
This model represents the zero-bias constant temperature reference value (a0), the linear temperature drift component (a1), and the non-linear temperature drift component (a2) through three coefficients. The parameters (a0, a1, a2) are fitted by least squares using 30 calibration points (−40 ~60 °C), with a fitting error of less than 0.02 mg. In the specific process, the zero-bias voltages (V1, V2) corresponding to different temperature points (T1, T2) are constructed as an observation matrix, and the coefficient vectors a0, a1, and a2 are solved using matrix operations (x = (ATA)−1ATb).
When using the least squares method, a matrix equation Ax = b is constructed, where:
At room temperature, the accelerometer is mounted on a high-precision indexer for calibration. Using the 12-position calibration method, the system identifies the zero-output positions for both measurement axes by rotating the indexing head. The X-axis zero-output position is designated as the 0° reference. During calibration, the indexer rotates in 30° increments, with ten output measurements collected and averaged at each position. To eliminate directional bias, the indexing head completes both clockwise and counterclockwise rotations. The final calibration values are obtained by averaging the corresponding angular outputs from both rotation directions. The complete calibration results are presented in Fig. 4.
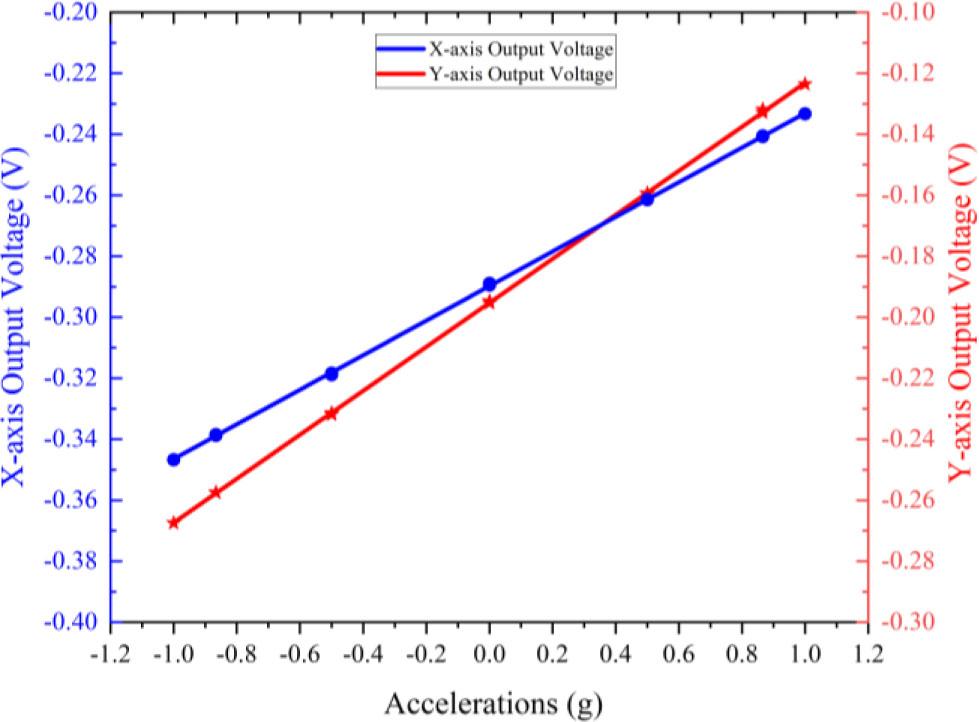
Output of the dual-axis accelerometer within the measurement range of ±1 g.
Fig. 5 shows the variation of the two axial outputs of the accelerometer with the angle of the high-precision indexer. When the angle of the indexer is 0°, the X-axis is at the zero-output position, and the Y-axis is at negative full-scale output. The outputs of the X-axis and Y-axis are sinusoidal as the indexer rotates one full cycle. The coupling coefficient of the X-axis to the Y-axis is 1.31 %, and the coupling coefficient of the Y-axis to the X-axis is 2.4 %.
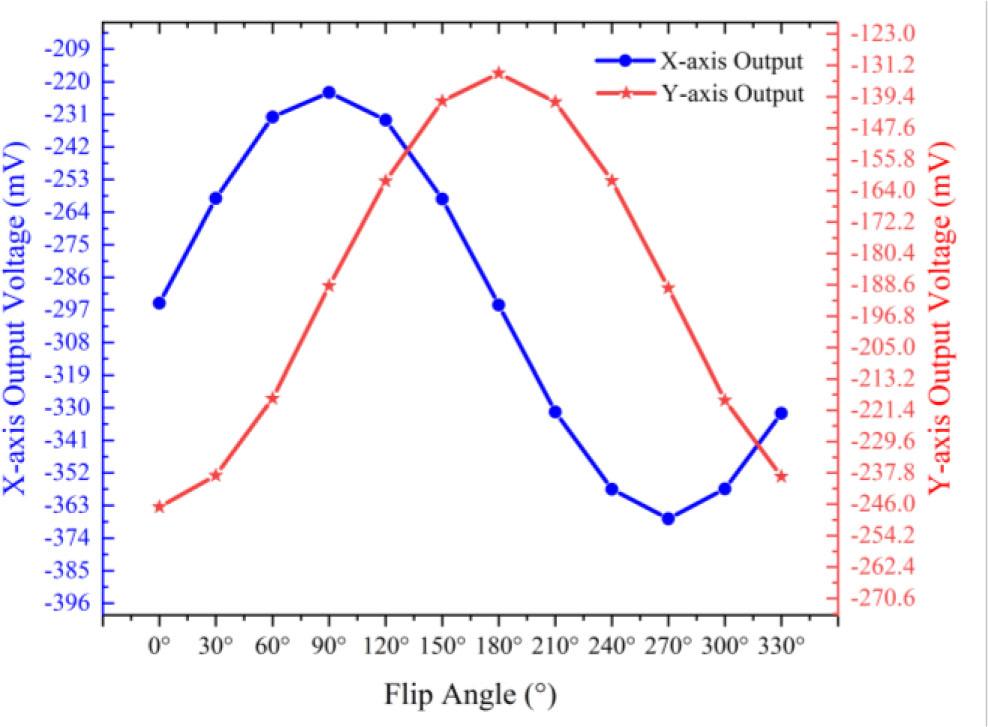
Output when the accelerometer rotates through one full cycle.
Before conducting temperature compensation, we need to perform temperature calibration for the accelerometer over the full temperature range to obtain the compensation coefficients used in the temperature compensation system. Fig. 6 shows the experimental setup for temperature calibration: (a) the physical structure of the nested dual-axis accelerometer (under test), and (b) the temperature chamber and data acquisition equipment used to control and monitor the ambient temperature.

Accelerometer structure and temperature experimental equipment: (a) Accelerometer structure; (b) Temperature experimental equipment.
For the calibration tests over the full temperature range, the device without temperature compensation is placed horizontally in the temperature chamber, and the accelerometer is turned on at room temperature until the output of the accelerometer stabilizes. By setting the temperature of the temperature chamber to different temperature environments, when the accelerometer output stabilizes, the ambient temperature at that time is measured, and data within 10 minutes of stable output are taken as reliable data. The entire testing system is controlled by a computer and the measured data are stored in real time. The final test results are within the range from −40 °C to 60 °C, with measurements taken at 10 temperature points. The temperature deviation at each data collection point does not exceed 0.5 °C. The test data are plotted as shown in Fig. 7.
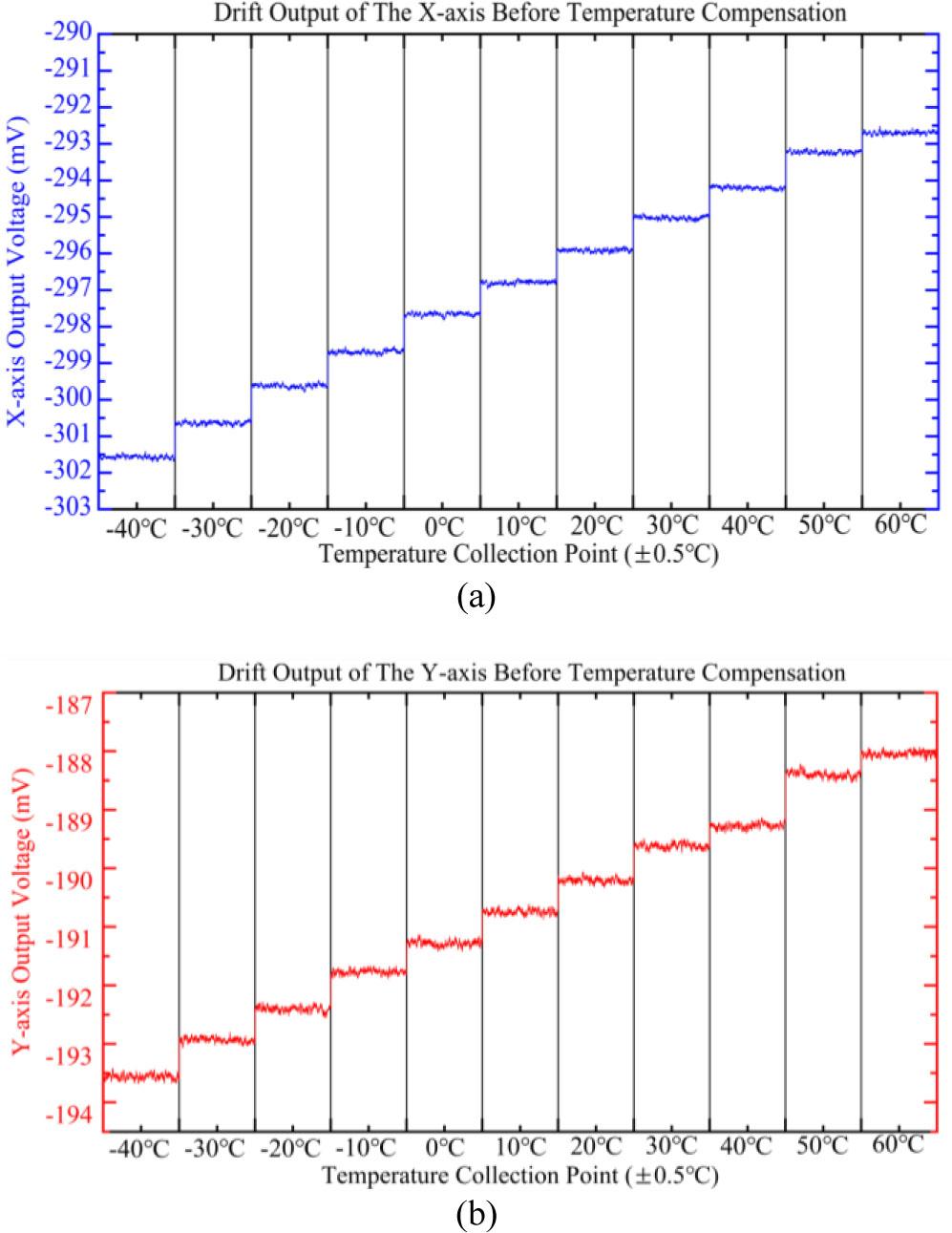
Stable output of the accelerometer at each point within the full temperature range before temperature compensation: (a) X-axis; (b) Y-axis.
Fig. 7 shows the accelerometer's stable output at different temperatures in the mechanical zero state. This output is converted to zero bias, with the results presented in Fig 8. Over the full temperature range, the X-axis temperature drift coefficient is 1.26 mg/°C, and the Y-axis is 0.91 mg/°C.
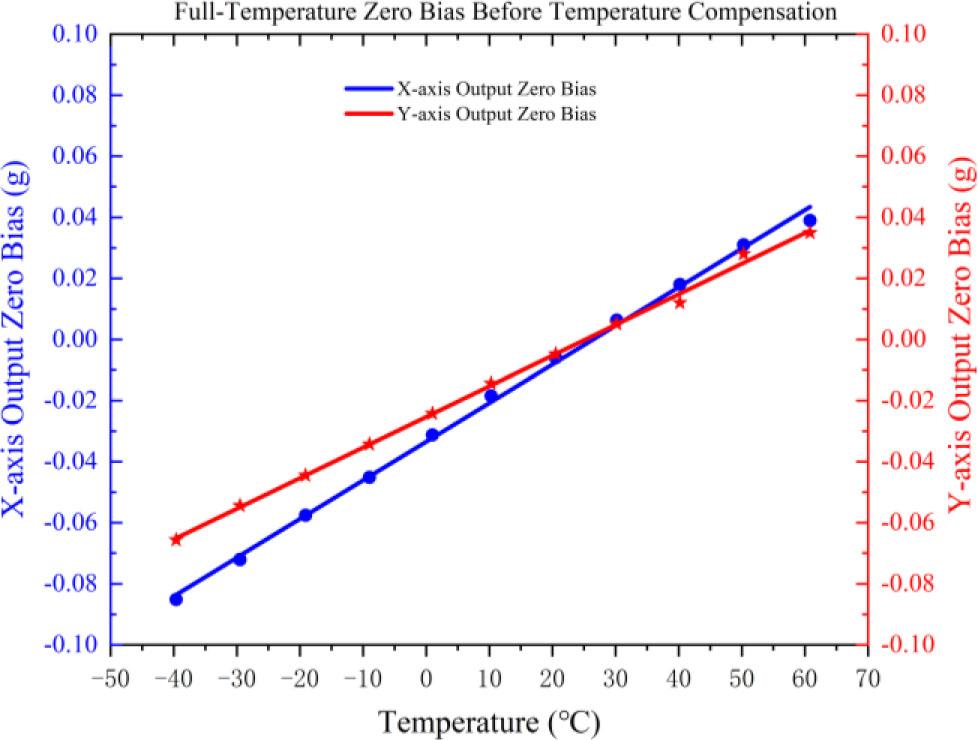
Bias stability of the accelerometer over the entire range before temperature compensation.
The above data demonstrate that the device already possesses good bias stability over the full temperature range under natural conditions. The sensor is then assembled with the temperature compensation module, as shown in Fig. 9.

Sensor and temperature compensation module.
A full temperature test is performed on this system again. The final output results are shown in Fig. 10 and Fig. 11. After temperature compensation, the temperature drift coefficient on the X-axis is 0.02008 mg/°C, and on the Y-axis is 0.02041 mg/°C over the full temperature range. Moreover, the expanded uncertainty (k = 2) for the X-axis drift after compensation is 0.003 mg/°C, and for the Y-axis is 0.0028 mg/°C, calculated from the combined standard uncertainty of temperature measurement (±0.5 °C) and output noise (0.001 mg).
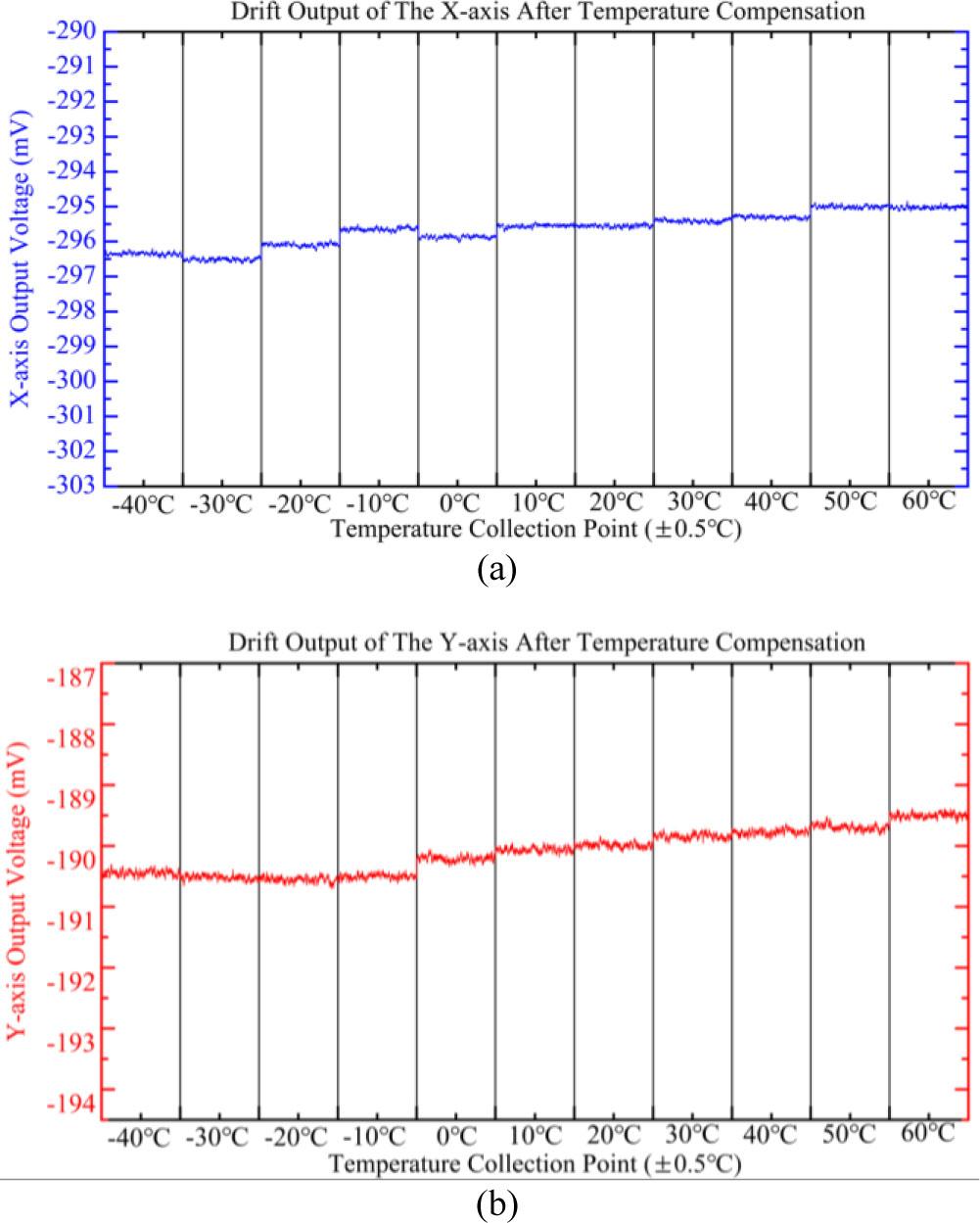
Stable output of the accelerometer at each sampling point within the full temperature range after temperature compensation.
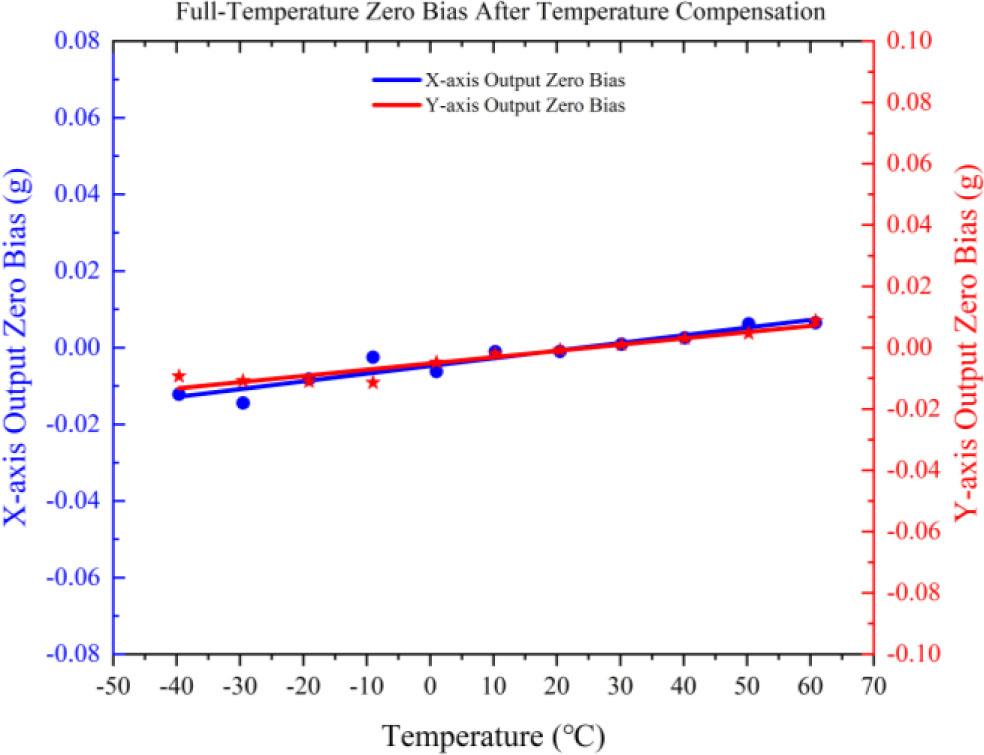
Bias stability of the accelerometer over the entire range after temperature compensation.
This work presents a nested dual-axis MEMS accelerometer integrated with closed-loop control and temperature compensation. After compensation, temperature drift coefficients are reduced to 0.02008 mg/°C (X-axis) and 0.02041 mg/°C (Y-axis), demonstrating significant performance improvement. Future work will focus on optimizing structural symmetry to further reduce non-linear errors and expanding applications in high-precision industrial measurement.