1. Introduction
The tabla, a pair of hand drums, is an essential percussion instrument of the North Indian classical and semi-classical music traditions. It comprises two drums, a bigger bass drum called the ‘bayan’ and a smaller-diameter treble drum called the ‘dayan’ (Figure 1). These drums can be struck in a variety of manners, individually or in combination, to produce sounds of distinct acoustic timbres, or gestalts, that are identified uniquely by a set of 10 – 20 (based on playing style and tradition) onomatopoeic syllables called ‘bols’. Automatic transcription for tabla has therefore generally been viewed as a monophonic timbre recognition task, identifying the sequence of tokens, or bols, corresponding to the played tabla strokes where a single bol can be realised by one or by two simultaneous strokes, one on each drum. This can be contrasted with the automatic transcription of western drums addressed in recent studies, which involves noting only the instrument in the drum kit that was struck, together with its onset time, in a polyphonic setting (Wu et al., 2018).

Figure 1
The tabla set – (left) bayan or dagga and (right) dayan or tabla.
While the number of tabla bols is large, depending also on the tabla player’s lineage and style, a useful classification of bols corresponds to their high-level musical role of marking the different beats in the rhythmic cycle, especially in the tabla accompaniment of vocals (Courtney, 2013). The categorization relates to whether the stroke is non-resonant (damped) or resonant, and further within the latter, which drum is struck (treble, bass or both). Table 1 shows the mapping of bols across the four stroke categories together with the type of constituent stroke on each drum and the resulting acoustic characteristics. The damped (D) stroke category includes all damped strokes played either on a single drum or together on both, but with no resonant stroke component. The resonant treble and bass (RT and RB) categories refer to strokes that are resonant on the corresponding drum and may further be accompanied by a damped stroke on the other. The resonant both (B) category consists of resonant strokes played simultaneously on both drums. The timbral variety within a category comes from the manner, pressure and position of striking the drum head leading to a diversity of acoustic characteristics within a class (Narang and Rao, 2017). In this work, we concern ourselves with the automatic detection of the four categories from the tabla audio recording. The motivation comes from our interest in vocal accompaniment where the time-keeping tabla player signals the different subsections of the rhythmic cycle by the presence or absence of right and left drum resonant strokes (Clayton, 2001; Courtney, 2013). The four-way classification has accordingly been useful in the empirical analyses of tabla accompaniment in khyal vocal performances (Clayton, 2020).
Table 1
The four target tabla stroke categories, their acoustic characteristics, constituent stroke types (resonant/damped/no hit) on each drum (bass and treble) and some typical bols in each category.
| TABLA STROKE CATEGORY | ACOUSTIC CHARACTERISTICS | CONSTITUENT STROKE TYPES | BOLS | |
|---|---|---|---|---|
| BASS | TREBLE | |||
| Damped (D) | No sustained harmonics, burst of energy at onset | No hit Damped Damped | Damped No hit Damped | Ti, Ta, Te, Re, Da, Tak, Tra Ke, Kat Kda |
| Resonant Treble (RT) | Strong onset followed by sustains F0 (>150 Hz) and harmonics | No hit Damped | Resonant Resonant | Na, Tin, Tun, Din Tin (Ke on bayan) |
| Resonant Bass (RB) | Weak onset burst followed by sustained F0 (~100 Hz) and few short-lived harmonics | Resonant Resonant | No hit Damped | Ghe Dhe, Dhi, Dhet |
| Resonant Both (B) | Combined characteristics of resonant treble and bass | Resonant | Resonant | Dha, Dhin |
As in the task of tabla bol transcription, timbre-based classification of the four categories can potentially be achieved with supervised learning from tabla audio labeled with the bol category and onset times. As also in bol transcription, the generalization to unseen instruments is a challenge arising from the variation in physical properties and tuning across tabla sets. We build on previous work that investigated deep learning techniques for the four-way tabla transcription based on the distinctiveness of timbres across the four categories (Rohit et al., 2021). The resonant bass (RB) class was especially challenging to detect, attributable to its inadequate representation in the dataset. Such data scarce contexts have been addressed in a number of different ways with transfer learning being among the more popular, aiming to reuse network parameters by transferring knowledge between domains (Choi et al., 2017). Motivated by this, Rohit et al. (2021) used an available pretrained Western drum stroke classification network and fine-tuned it to have the hi-hat, snare and kick drum output nodes predict the tabla stroke categories D, RT and RB respectively. A marked improvement was observed in performance for the RB class from the use of transfer learning. In the current work, we propose new methods that more closely exploit the correspondence between the tabla bol categories and Western drums to explore further overall task performance gains. We use available drum datasets to pretrain models and investigate data augmentation techniques for the tabla audio and also for the drum-pretraining datasets to determine ways to improve the acoustic match between the two culturally distinct percussion instruments.
We find that drum-pretraining results in better tabla stroke classification performance compared to a randomly initialised model, pointing to the promise of drum data for the tabla stroke classification task. Subsequent finetuning of the drum-pretrained model on tabla data leads to large improvements in performance, as expected from this transfer learning context. However, our experiments, as reported in this work, show that the performance of the finetuned model does not generally surpass the corresponding model trained from scratch on the tabla data but for the case of one of the stroke categories, namely the resonant treble.
The rest of the paper is organized as follows – after a brief survey of previous work on tabla bol and stroke-category classification in Section 2, we describe our datasets in Section 3. In Section 4, we present discussions of the new classification system, the CNN model architectures, experiments involving pretraining on suitably modified and augmented Western drum data, and finally a new data augmentation method for tabla resonant bass. In Sections 5, 6 and 7, the evaluation methods and results are discussed and summarized.
2. Previous Work
Among the two main formats of tabla playing – solo and accompaniment (to a melodic lead), the former entails the presentation and improvisation of tabla compositions, while accompaniment involves the playing of the fairly fixed cyclic stroke sequence known as the theka. Due to the high diversity and richness of bol content in compositions, bol classification has been mainly limited to tabla solo playing, except for the works of Sarkar et al. (2018) and Shete and Deshmukh (2021), that looked at recordings of the theka of different tals (akin to the metre). Given our specific interest in tabla in vocal performance and recognising the difficulty of obtaining training data for this context, we consider training our models on the more amply available tabla solo recordings and evaluate the models on our target of tabla accompaniment audio.
The most common approach to bol classification has been to address the problem in two parts – first detecting stroke onsets and then using acoustic features extracted from stroke segments to train supervised bol classification models. In the earliest work on tabla transcription, Gillet and Richard (2003) modelled the power spectra of stroke segments using a Gaussian mixture model (GMM), and used the GMM parameters to train a hidden Markov model (HMM) for 10-class bol recognition. The GMM was initialized using the mean and standard deviation of the stroke’s power spectrum in disjoint frequency bands that captured tabla bass and treble harmonic regions. While high classification accuracies were obtained, the dataset used was rather small and had a limited variety of playing styles and tempo.
Building further, Chordia (2005) made use of a large set of acoustic features, inspired from timbre recognition tasks such as instrument classification, to train neural network classifiers on a larger and more realistic dataset. Classification performance was heavily influenced by the particular tabla set that the model was tested on and tended to be low on instruments not seen during training. There have been more recent studies along similar lines, making use of classifiers like decision tree and support vector machines trained on common low-level acoustic features (Sarkar et al., 2018; Shete and Deshmukh, 2021). A main drawback of these models is that they are trained on small datasets, often with individual recordings of strokes from a single tabla and not realistic continuous playing where strokes overlap in time.
Extending the bol transcription task to a pattern retrieval application, Gupta et al. (2015) designed a system to transcribe tabla playing with the goal of identifying instances of common bol sequence patterns. For the transcription, a GMM-HMM system was trained on frame-wise mel-frequency cepstral coefficients (MFCCs). Although the training dataset was realistic in that it contained harmonium accompaniment in the background, the recordings were made on a single tabla and the system is therefore unlikely to perform well on new instruments.
In an attempt to perform the musicologically motivated classification of strokes played in tabla accompaniment (as opposed to solo), a four-way classification task was previously defined for the four categories rather than the usual 10–15 bols (Rohit and Rao, 2021; Rohit et al., 2021). This was motivated by recent empirical studies investigating bass- and treble-drum specific accenting found in the cyclic theka played by tabla in accompaniment to vocal or instrumental lead (Clayton, 2020; Srinivasamurthy et al., 2017). To address the four-way classification task, Rohit and Rao (2021) built a system that first detected onsets and then used a random forest classifier trained on the extracted low-level acoustic features to identify the stroke category. The features included novel decay-related characteristics of treble and bass frequency harmonics which ranked higher in importance relative to the more commonly used features. Moving to automatic feature learning and inspired by automatic drum transcription (ADT) methods, Rohit et al. (2021) explored convolutional neural networks (CNNs) for the prediction of onsets of each category. By exploiting the approximate acoustic correspondence between tabla stroke categories and the three popular western drums (hi-hat, snare and kick), transfer learning was explored to adapt an available pretrained multi-label (three-class) ADT model to tabla stroke classification. The model was fine-tuned to predict onsets of D, RT and RB, while B onsets were obtained by identifying simultaneous onset predictions of RT and RB. Also investigated was a trained-from-scratch bank of four single-category (binary) CNNs, individually optimized to predict the onsets of each tabla stroke category, also inspired by ADT research. This architecture was found to surpass the overall performance of the fine-tuned three-way ADT model, with the use of tabla-specific training data augmentation methods improving it further.
Both the random forest and the CNNs were tested on realistic tabla accompaniment recorded in isolation, but due to the expensive nature of creating such a dataset, they were trained on more easily available tabla solo data. With both methods, a considerable gap in the train and test classification performance was observed, possibly due to lack of sufficient training data and a mismatch in the playing styles of the two formats. Interestingly, the use of a pretrained and fine-tuned drum-model was found to particularly benefit test set performance for the tabla resonant bass category, which also had the least training data available. Motivated by this success of each of transfer learning and data augmentation when used independently, we investigate the synergetic benefit from applying them together in the current work. We also revise the tabla-to-drum stroke mappings for better exploitation of the available training data.
3. Dataset
A summary of the different sources for the tabla and drum training and testing datasets used in this work appears in Table 2. All audio files (of both tabla and drums) were formatted to single-channel, 16 kHz sampling rate and 16 bit depth. We provide a brief review of the relevant aspects of the datasets in this section.
Table 2
Description of the train and test datasets for drums (Gillet and Richard, 2006; Southall et al., 2017b; Dittmar and Gartner, 2014) and tabla (Rohit et al., 2021).
| INSTRUMENT | DATASETS | INSTRUMENTS | DURATION |
|---|---|---|---|
| Tabla | Train/Val: Solo | 10 | 76 min. |
| Test: Accompaniment | 3 | 20 min. | |
| Drums | Train: ENST+MDB | 26 | 163 min. |
| Test: IDMT | 4 | 123 min. |
3.1 Tabla
The tabla instrument diversity (in terms of number of distinct instruments recorded and the range of their tuning pitch) represented in recent work (Rohit and Rao, 2021; Rohit et al., 2021) improved considerably upon that reported in any similar previous literature, and is therefore adopted for the present work. With the primary goal of classifying strokes played in tabla accompaniment (as opposed to tabla solo), the test set comprises recordings of expressive tabla played as accompaniment to vocals but recorded in perfect isolation to limit the complexity of our task. Since most public concert audio, even if available in multi-track format, contains bleed from other instruments, these recordings were created specially for the task. For this, recordings of solo singing were first obtained from expert singers. Then, tabla artists played the corresponding accompaniment while listening to the vocals over headphones, and their playing was recorded. There are a total of ten tracks spanning a net duration of twenty minutes and yielding about 4500 strokes. The expressive nature of tabla accompaniment (lacking a fixed score and containing extempore fillers) makes the annotation of this audio challenging. The audio was labelled by first running an automatic onset detector based on the high-frequency content algorithm (Brossier et al., 2004) to obtain stroke onsets, followed by manually assigning the four-way labels by listening to the audio and visually inspecting the spectrogram. Annotation was carried out by a tabla artist and cross-checked by one of the authors of the paper.
Due to the intensive nature of obtaining and annotating such tabla accompaniment recordings, 76 minutes of the more easily obtained tabla solo playing is used as training and validation data. This dataset comprises about 26,600 strokes rendered in solo compositions recorded from across 10 distinct tabla sets. To ensure adequate diversity of training data, instruments of sufficiently different tuning were chosen, and a variety of compositions played over a wide tempo range was included. Audio files were annotated by first running an automatic onset detector, then automatically aligning the corresponding bol sequence supplied by the players (as composition scores) with the onsets, and finally replacing bols with four-way labels following the assignment shown in Table 1. Although tabla bol-stroke mapping is fairly unique, there are exceptions. The same bol (e.g., Na) can sometimes be used to refer to strokes of very different types (resonant treble or damped). Hence, additional manual verification was required in order to assign the correct four-way label based on the actual sound production.
While the accompaniment-style test dataset is relatively small in size (20 minutes), the availability of the larger tabla solo dataset serves us well as a training dataset while also facilitating the more reliable testing of within-style classification in cross-validation mode.
3.2 Drums
We used two publicly available drum datasets containing real (as opposed to synthesized) drum-only tracks and polyphonic mixtures – ENST (Gillet and Richard, 2006) and MDB Drums (Southall et al., 2017b). For the current study, the drum-only tracks were used. From the ENST dataset, we use all tracks containing onsets of the three drums HH, SD and KD. We found in our initial experiments that they were a better match to our tabla data compared to any of the synthetic drum data. Our pretrained drum model is also evaluated on the IDMT-SMT drum dataset (Dittmar and Gartner, 2014) to confirm ADT performance comparable to the state of the art. This set consists of 123 minutes of both real and synthetic drum-only audio, and has been widely used as a test set in ADT research.
4. Methods
With a goal of accurate detection of tabla strokes according to the four musicological category labels in Table 1, Rohit et al. (2021) obtained their best performance with a CNN model trained separately for each category on the tabla solo training data. In this work, we adopt a similar model but with a sound production-based approach, viewing any bol in terms of the three contributing ‘atomic’ strokes, namely the resonant treble (termed ‘RT-any’), resonant bass (termed ‘RB-any’) and damped (termed ‘D’). A CNN model is trained for each atomic stroke with the bol instances in the dataset contributing potentially to more than one class as presented in Table 3. The D model, however, is trained only on the purely damped bols since the reduced four-category annotation of the training dataset does not always provide information about the presence or absence of a damped stroke (see RB and RT rows in Table 1). The resonant treble (RT-any) and bass (RB-any) models are trained not only on RT and RB strokes (respectively), but also on B strokes (‘Dha’, ‘Dhin’).
Table 3
The list of bols used to train the models for each of the atomic strokes. In bold are bols common to more than one atomic stroke.
| MODEL | BOLS USED FOR TRAINING |
|---|---|
| D | Ti, Ta, Te, Re, Da, Tak, Tra, Ke, Kat, Kda |
| RT-any | Na, Tin, Tun, Din, Dha, Dhin |
| RB-any | Ghe, Dhe, Dhi, Dhet, Dha, Dhin |
Rohit et al. (2021) reported an improvement in tabla stroke classification performance with the use of tabla-specific data augmentation methods, along with standard pitch-shifting and time-scaling. These methods included spectral filtering and stroke remixing. Spectral filtering involved modifying the overall balance between low and high frequencies to emulate variations in instrument-related acoustic characteristics as validated by a tabla instrument classification experiment. Stroke remixing used non-negative matrix factorization (NMF) to decompose tabla audio into the three atomic strokes (damped, treble, bass) followed by recombination with different weightings to simulate expressive variations and different artistic and playing styles. We continue to use the same tabla data augmentation in the present work and additionally investigate a new method specific to RB strokes.
Figure 2 is a block diagram of the system that illustrates the four-way classification ensuing from the three models. During inference, frame-wise onset detection functions (Bello et al., 2005) are obtained at a track-level from all three models. Outputs of RT-any and RB-any models are processed further to identify the onset pairs that comprise a ‘both’ (B) category bol based on their temporal proximity. In the absence of available knowledge on the expected separation of left and right drum strokes that constitute a compound bol, we experimentally tune a ‘maximum separation’ parameter as presented in Section 5 to find that 40 ms leads to the best detection f-score across resonant category strokes. Any onset detection by the damped stroke model is retained as long as no other stroke is detected in the same frame.
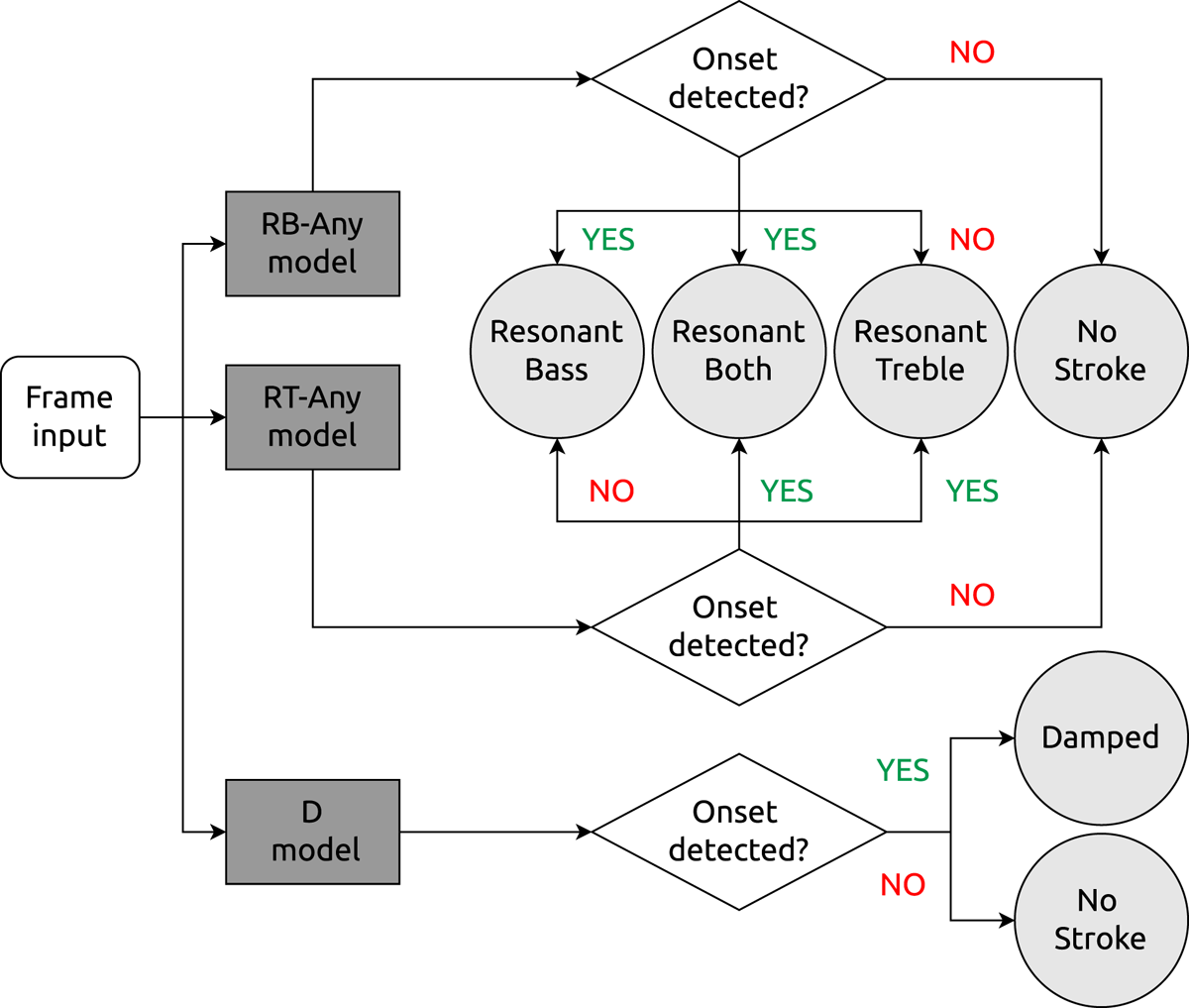
Figure 2
Schematic of the four-way classification system using three one-way CNN models to predict presence of atomic strokes (D, RT-any and RB-any) in a given audio frame. If both RT and RB onsets are detected then the onset is marked B. Any D that co-occurs with RT or RB is ignored.
To investigate the utility of using Western drum data, we conduct experiments where the same models are first pretrained on drum data and then fine-tuned on tabla solo data augmented using previously proposed signal modification methods. These models are referred to as ‘fine-tuned’ models. We also experiment with available drum data augmentation methods that could potentially improve the match to tabla. As a baseline, we retrain a randomly-initialised model entirely on the augmented tabla solo data. We refer to this as ‘retraining’. Finally we introduce a new tabla bass-specific data modification method that is evaluated with both the retrained and fine-tuned models.
4.1 CNN model architectures
The classification models for each stroke are CNNs that operate on short excerpts of the log-scaled mel spectrogram to produce a value between 0 and 1 indicating the probability of an onset in the center frame of the input. The general architecture is highlighted in Figure 3, and the hyperparameter values related to the model architecture for each stroke are detailed in Table 4. These values are based on previously suggested model architectures for tabla and drum transcription tasks (Rohit et al., 2021; Jacques and Röbel, 2018). The RB-any model consists of two convolutional layers with 16 and 32 filters respectively and a penultimate dense layer with 128 units. For RT-any, the number of filters in the two convolutional layers is doubled to 32 and 64 respectively. For D, the number of units in the dense layer is doubled to 256.

Figure 3
General CNN model architecture for all experiments.
Table 4
Hyperparameter values for the CNN model architecture (of Figure 3) used for each stroke category.
| MODEL | HYPERPARAMETERS |
|---|---|
| D | N1=16, N2=32, N3=256 |
| RT-any | N1=32, N2=64, N3=128 |
| RB-any | N1=16, N2=32, N3=128 |
The input time-frequency representation, borrowed from previous work on onset detection (Schlüter and Böck, 2014) and drum transcription (Jacques and Röbel, 2018) tasks, is a stack of three log-scaled mel-spectrograms (‘channels’) computed using sliding Hann windows of sizes 23 ms, 46 ms and 92 ms respectively, with hop size fixed to 10 ms in all cases. The dimensions of each channel in the input are 80 mel–frequency bands and 15 time-frames, similar to the values used by Schlüter and Böck (2014) and Jacques and Röbel (2018). While the model predicts the presence of an onset for the center frame, the remaining frames serve as useful context. The model output is compared against a binary target – onset (1) or no-onset (0). Since onset events are not strictly single-frame events, we use target smearing (Schlüter and Böck, 2014) during training to capture this temporal spread of onset energy – frames immediately adjacent to every onset frame are also considered onsets but are weighted 0.5 (while other frames are weighted 1) in the loss computation. The loss function minimized is the binary cross entropy between frame-wise onset predictions and binary targets. All models are trained using the Adam optimizer (Kingma and Ba, 2015) with a batch size of 256 for a maximum of 150 epochs. Early stopping with a patience of 10 epochs is used to save the model with the lowest validation loss.
The tabla training data is augmented using the best-performing method from Rohit et al. (2021), which combines four augmentation methods – pitch-shifting, time-scaling, spectral filtering, and stroke remixing. During inference, an onset detection function is obtained for a given audio track by concatenating frame-wise model outputs. A fixed-threshold peak-picking algorithm (Bello et al., 2005) is then used to binarize the onset detection function and obtain a transcript containing the temporal locations of the predicted onsets.
4.2 Drum pretraining and fine-tuning with tabla
To exploit the possible similarities between the four-way tabla stroke classification and the three-drum ADT tasks, the three CNNs corresponding to D, RT-any, and RB-any are each first trained to respectively predict onsets of hi-hat, snare, and kick drums. Figure 4 depicts the pretrained networks and also shows the acoustic similarities between the mapped drum and tabla strokes via the spectrogram images. The hi-hat is known to exhibit a variety of acoustic characteristics depending on how it is struck, but, in this work, we employ a single label for all hi-hat strokes. Next, the models are fine-tuned on tabla data using the ‘uniform’ method from Rohit et al. (2021), which refers to tuning all the layers simultaneously at the same learning rate. The use of other approaches involving differential learning rates or freezing some layers of the model was not found to provide any improvements in initial experiments. We experiment with two values for the initial learning rate, 10–4 and 10–5, to allow a lower learning rate to potentially help better preserve the useful drum-related features learned during pretraining. The learning rate which results in the model achieving higher cross-validation f-scores is used for testing and reporting results.
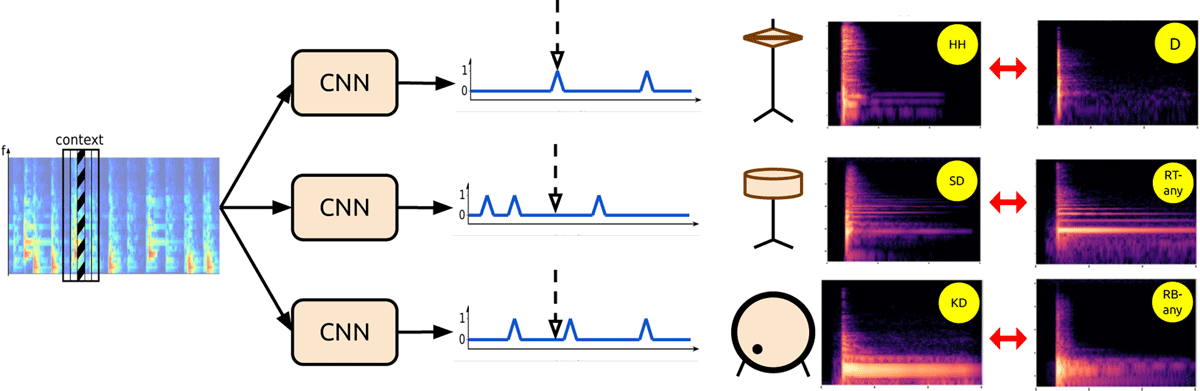
Figure 4
The transfer learning approach where the three one-way CNNs are first pretrained to predict single drum onsets and then fine-tuned on corresponding tabla stroke category data. Model input is a small portion of a track’s spectrogram and the output is the onset prediction for the center frame. Figure inspired by Vogl et al. (2017). The final spectrogram pairs demonstrate the acoustic similarity across the mapped source and target classes.
4.3 Drum data modification and augmentation
To provide a better match between drum and tabla data for the pretraining and fine-tuning experiments, we consider making some modifications to the drum dataset. These are based on the observed differences in tabla and drum stroke distributions as shown in Figure 5. We note that HH onsets in the training set are equally distributed among isolated HH strokes and those that occur along with SD/KD. For tabla D strokes, since the ground truth labels exclude those occurring with RT/RB, we do not have data about this proportion. Nevertheless, since the model is required to only identify isolated D onsets, pretraining it to similarly predict only isolated HH onsets could be more fruitful. Next, comparing RT-any and RB-any with SD and KD, we find that tabla resonant strokes are rendered together as (or more) frequently than they are played singly or along with a damped stroke. With drums, most onsets of SD and KD do not co-occur with the other drum’s onset (based on a 40 ms neighbourhood criterion; choice of 40 ms is explained in Section 5). This is attributed partly to the higher number of single-drum tracks in the drum dataset but also to the fact that the snare and kick drums occur on different beats in many common drum grooves. To address the potential dataset mismatches, we make two modifications to the drum data: (1) HH onsets co-occurring with SD/KD are discarded and only isolated HH onsets are used (‘HH-only’); (2) For SD and KD model training, frames containing simultaneous onsets of SD and KD are repeated thrice in order to achieve proportions more similar to tabla data (‘SD-KD data repeat’).
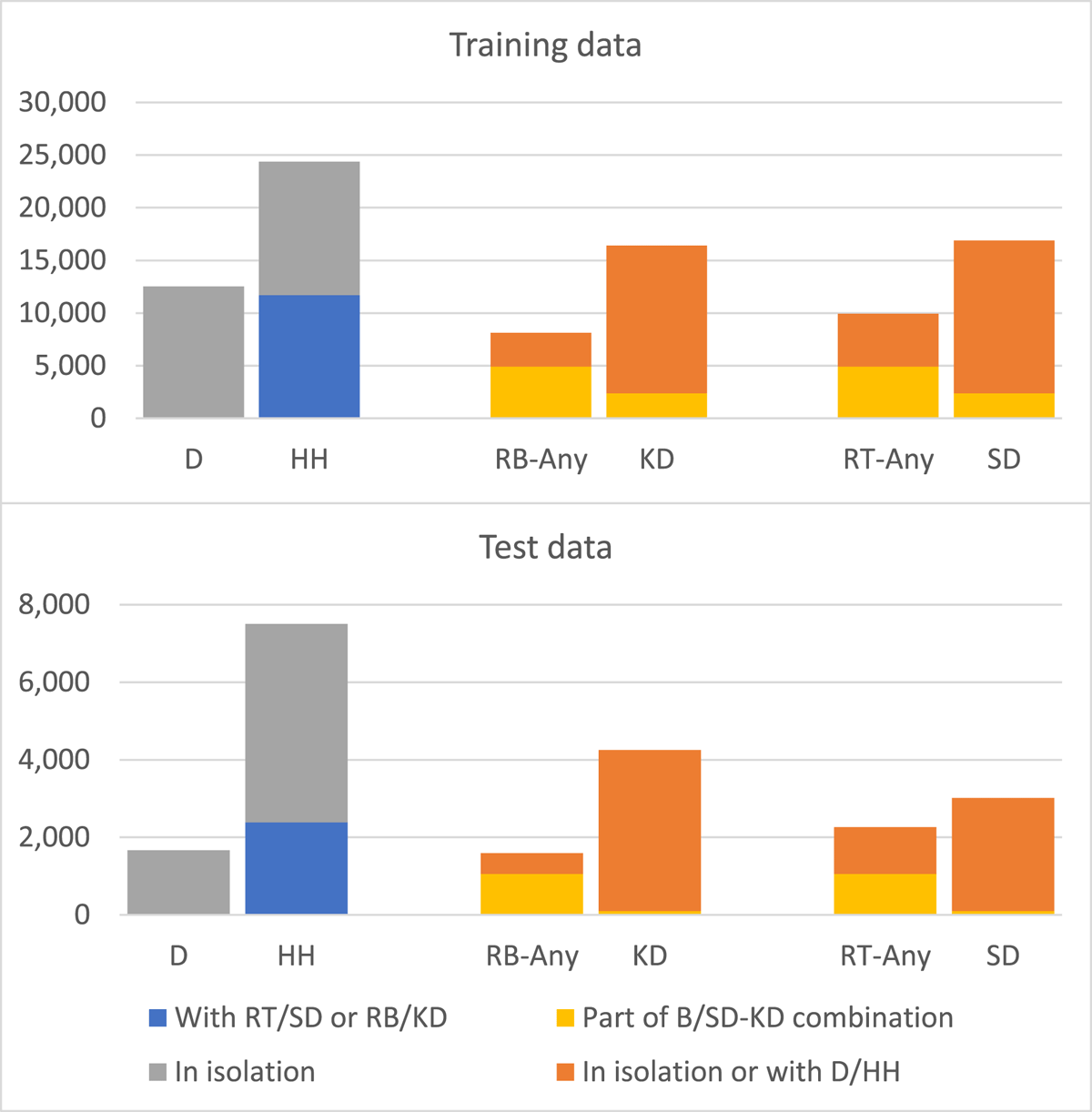
Figure 5
Distribution of drum and tabla strokes in the training and test datasets across the various drum and tabla stroke categories.
We also experiment with drum augmentation methods with a goal of improving the acoustic match with tabla data. For SD and KD, pitch-shifting (‘PS aug’) and resampling (‘RS aug’) are applied on all the audio tracks in the dataset, prior to training, with each method generating four fixed versions of every audio signal, corresponding to pitch transpositions of –200, –100, 100, and 200 cents. These methods were previously shown to work well for SD and KD classification (Jacques and Röbel, 2019). Although a noise remixing method was found to work best for SD, it is not considered here due to the lack of a publicly available implementation. Pitch-shifting is performed using the ‘hptsm’ algorithm from the python library ‘pytsmod’ (Yong et al., 2020) that was previously found to be more appropriate for sounds with harmonic and percussive components such as tabla and drums (Rohit et al., 2021). For resampling, the audio is resampled with factors 0.89, 0.94, 1.06, and 1.12, and saved at the original sampling rate. This operation, in addition to changing pitch by the same transposition values as in pitch-shifting, also affects signal duration. The ground truth for resampled audio is modified suitably to accurately point to the new onset locations. With the input length to the CNN during training kept fixed at 150 ms, input training examples from the resampled audio are still of the same dimensions but capture a longer or shorter musical context due to the time-scaling.
For HH classification, the addition of Gaussian noise was previously found to maximize classification performance (Jacques and Röbel, 2019). However, based on the less noisy nature of tabla D strokes (as also evident in Figure 4), adding noise is not expected to be helpful for D classification. Hence, we chose to experiment with a random spectral filtering method as used by Schlüter and Grill (2015) for singing voice augmentation. This method is also quite similar to the spectral tilt modification that was previously found to be effective for D stroke classification (Rohit et al., 2021). Random filtering augmentation (‘RF aug’) is performed during runtime by multiplying every frame of the log mel-spectrogram training samples of HH with a Gaussian filter. The filter’s mean, standard deviation, and amplitude are randomly chosen for each training sample from the following ranges: [150, 8000] Hz, [5, 7] semitones, and [–10, 10] dB, respectively. One augmented version of every training sample is generated.
4.4 Retraining
Retraining refers to training the same CNN models from scratch, with a random initialization of model weights, on the available tabla solo training data. This affords us an important reference by which to judge the efficacy of the transfer learning for the tabla task. The initial learning rate for the retraining is fixed to the larger value of 10–4.
4.5 Tabla augmentation with bass modulation
A common technique for imparting expression in tabla playing is the modulation of the bass drum pitch in RB and B strokes by varying the pressure applied by the wrist on the membrane (Rohit and Rao, 2018). Such modulation can be classified into one of three broad types – flat, up, or down modulation (Courtney, 2013), which result respectively in a flat, upward-going, or downward-trending bass F0 contour, as shown in the example spectrograms of Figure 6. Introducing more such realistic variations in the F0 contour of bass strokes in a tabla training dataset could help generalization of the stroke classification. This is achieved by deriving prototypical F0 contours from the training data bass strokes and then creating multiple resynthesized versions of each stroke by the replacement of the F0 contour.
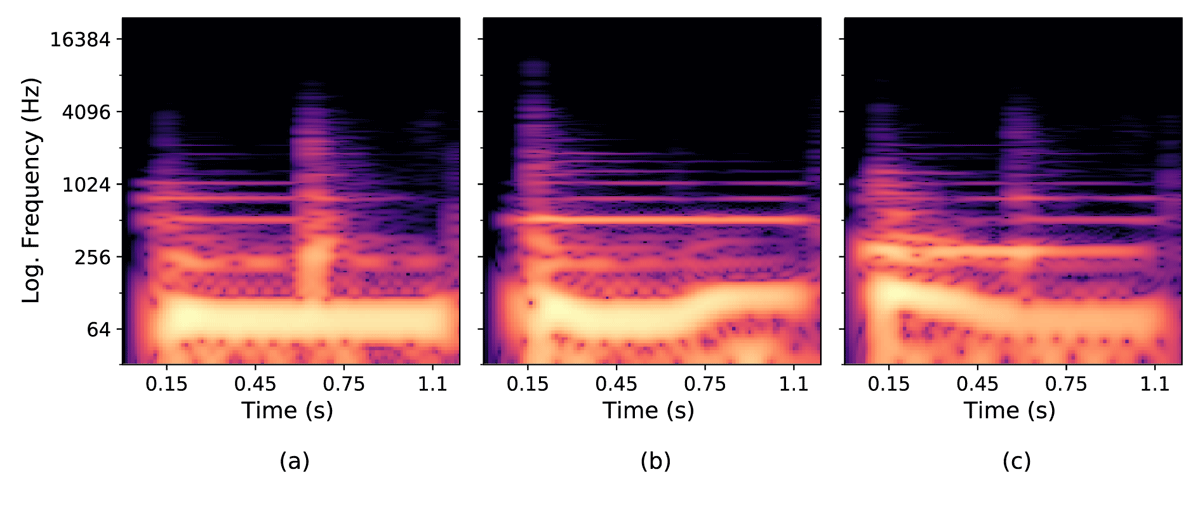
Figure 6
Spectrograms of resonant both tabla strokes showing the common F0 modulation types for the constituent resonant bass stroke: (a) No modulation, (b) Up modulation, and (c) Down modulation (ignore accompanying resonant treble harmonics and bursts of energy between 0.45–0.75 seconds in (a) and (c) from onsets of subsequent strokes on the treble drum).
To obtain the F0 contour templates corresponding to the various types of modulation, all bass stroke F0 segments are subject to a k-means clustering procedure. The F0 contour itself is estimated by decomposing the audio signal using a sinusoidal + residual model (Bonada et al., 2011), and selecting the sinusoidal component lying in the expected bass F0 range of 80 – 200 Hz. Prior to clustering, extracted F0 contours are length-normalized to the median duration using a Fourier-based resampling method provided in the python library ‘scipy’ (Virtanen et al., 2020), and pitch-normalized by transforming to the cent-scale (with respect to the contour’s minimum frequency). The cluster centroids obtained by fitting a k-means model with five clusters provided the best visual representation of the three modulation types and their significant variations as shown in Figure 7; the legend indicates the fraction of all strokes (out of a total of nearly 8000) assigned to each cluster. We observe that up-modulation (colored red) occurs less often while the flat contour and its slightly more concave variant are together the most common.
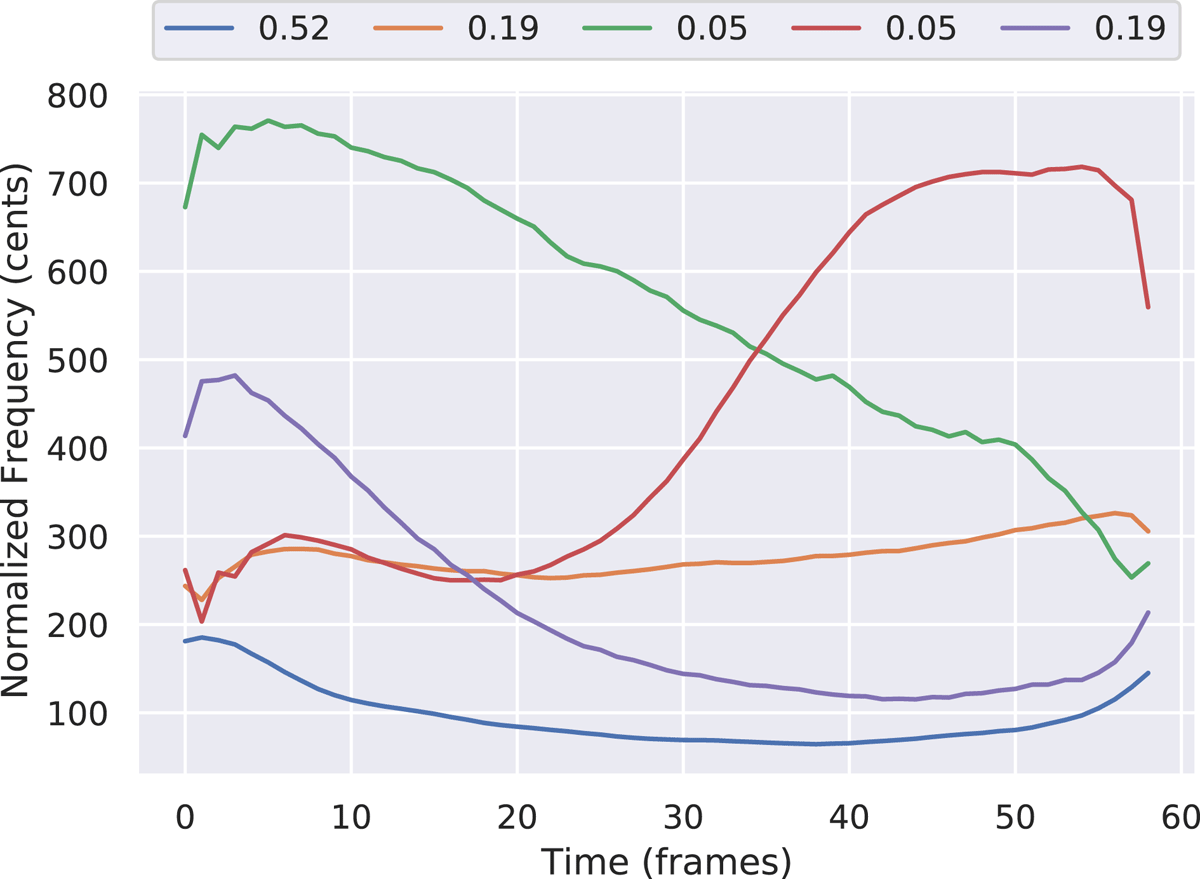
Figure 7
The five cluster centroids resulting from the k-means model fitted on resonant bass F0 contours of the tabla training dataset. The legend shows the fraction of data points assigned to each cluster.
Augmentation of training data (‘Bass mod aug’) is achieved by modifying the F0 contour of every bass stroke segment in a training set track. After first performing a sinusoidal + residual decomposition, the bass F0 contour is extracted and assigned into one of the five clusters. To modify the contour, one of the other four cluster centers is chosen and the F0 values in the bass stroke frames are replaced with the chosen contour (after suitably de-normalizing its length and frequency values), followed by the resynthesis with the originally extracted onset and treble harmonics. Informal listening confirmed that this process does not generate audible artifacts. We repeat this four times on each audio track and a different template contour is selected each time, giving four augmented versions of each training set audio.
5. Evaluation
The training dataset of tabla solo tracks in Table 2 is split into three cross-validation (CV) folds in an instrument-independent manner, i.e. no two folds contain tracks from the same tabla. The folds have similar distributions of stroke category, tabla tuning, and playing tempo. The three resulting models from each training fold are used as an ensemble on the test set of tabla accompaniment. Predicted onsets that lie within 50 ms of the ground truth are considered hits, while the rest are declared false alarms (Dittmar and Gartner, 2014). An f-score (harmonic mean of precision and recall) value is obtained through computations on the detected onsets versus ground-truth targets across all the tracks. While 50 ms tolerance is fairly large, re-evaluating our predictions at a reduced tolerance of ±20 ms is found to reduce f-scores by no more than 1% across systems. The peak-picking threshold that yields the highest CV f-score is used for the final reporting of CV and test set f-scores.
Onsets are first detected separately from the outputs of the three models D, RT-any, and RB-any. Following this, onsets of B category are obtained by detecting simultaneous RT-any and RB-any onsets as presented in Figure 2, to achieve the four-way classification. The maximal separation between RT-any and RB-any onsets for them to be considered a compound stroke onset is tuned experimentally. The results of this experiment are summarised in Table 5 where the models were pretrained on unmodified drum data and fine-tuned on the augmented tabla data. The mean f-score is reported for various values of the assumed maximum temporal separations between the bass and treble strokes {10, 20, 40, 80, 160} ms. We see that the f-scores do not change much in the broad range of 20 ms to 80 ms but fall off steeply beyond this, pointing to the clear acoustic distinction between the two interpretations of the closely occurring bass and treble strokes as a single compound bol or two separate bols. We settle for 40 ms as our algorithmic choice for the maximum separation between strokes to be considered as one bol.
Table 5
Mean CV F-score of RT, RB and B classification using different tolerance windows for combining simultaneous RT-any and RB-any onsets to B. The models were pretrained on unmodified drum data and fine-tuned on tabla data.
| Tolerance (ms) | 10 | 20 | 40 | 80 | 160 |
| Mean F-score (RT, RB, B) | 69.0 | 73.3 | 73.8 | 73.9 | 67.0 |
In summary, the models are evaluated in two ways. First, based on their individual predictions of D, RT-any and RB-any onsets. Second, based on the combined prediction of D, RT, RB, and B stroke categories (after replacing simultaneous RT-any and RB-any onsets with B, and simultaneous RT-any/RB-any and D onsets with RT-any/RB-any). Apart from providing a performance evaluation of the individual atomic stroke models, the first stage allows us to choose the individually best D, RT-any and RB-any models from across experiments, potentially leading to the best four-way classification f-scores.
6. Results and Discussion
Our approach in this paper has been to obtain the classification of each of the three atomic strokes with the best use of the available four-way labeled dataset, and then use the combination of classifiers in the eventual four-way task (D, RT, RB, B). Accordingly we present the results of our experiments as follows: (a) pretraining the three atomic stroke classifiers. This is followed by fine-tuning with augmented tabla data. We present results from the different pretrain and fine-tune data variations. Next presented is the retrained system performance with the three atomic models trained solely on the tabla dataset. Finally, we report the four-category classification for the best set of the three atomic classifiers from the fine-tuning and retraining experiments in terms of variations in drum-pretraining and tabla augmentation. This is benchmarked with the previous work (Rohit et al., 2021) that used the direct classification of the four categories trained and tested on the same tabla datasets.
6.1 Classification of the atomic strokes
The f-scores of D, RT-any, and RB-any classification using models pretrained on the original drum data and after applying additional modifications and augmentations are presented in Table 6. For reference, in the first two rows, we present results corresponding to an untrained network (that is, the chance lower bound computed from the onset distribution of each stroke type in the training data) and the drum-pretrained model (without drum data modification or augmentation). The next few rows record the improvements from fine-tuning the drum model and its data-augmented versions with the tabla training data. Comparing the first two rows, we find, not surprisingly, that pretraining on drum data improves tabla stroke classification performance compared to an untrained model. Subsequent fine-tuning on tabla data (rows 3-3g) pushes the f-score even higher, as expected.
Table 6
CV f-scores comparing stroke classification performance of the three atomic strokes (D, RT-any and RB-any) with the differently trained models of this work. ‘Untrained’ represents a model with random weights. Indentation in ‘Method’ column represents nested experiments. Values in bold are the highest in each column. An asterisk represents a significant difference (p < 0.001) between the f-scores of the best fine-tuned (selected from rows 3–3g) and the corresponding retrained model (of row 4).
| METHOD | D | RT-ANY | RB-ANY | |
|---|---|---|---|---|
| 1 | Untrained | 24.0 | 19.0 | 15.6 |
| 2 | Drum-pretrained | 55.6 | 37.1 | 28.8 |
| 3 | Fine-tuned | 88.3 | 92.9 | 87.7 |
| 3a | + HH only | 88.3 | – | – |
| 3b | + RF aug | 88.5 | – | – |
| 3c | + SD-KD data repeat | – | 93.1* | 88.1 |
| 3d | + PS aug | – | 93.0 | 88.8 |
| 3e | + Bass mod aug | – | – | 87.4 |
| 3f | + RS aug | – | 92.7 | 87.2 |
| 3g | + PS, RS aug | – | 92.4 | 86.8 |
| 4 | Retrained | 88.2 | 91.9 | 88.3 |
| 4a | + Bass mod aug | – | – | 88.2 |
The final two rows of Table 6 present the f-scores from the three atomic models trained solely on the tabla training data. The new bass augmentation does not help the retraining scores. The retraining f-scores are somewhat lower than those obtained from the best fine-tuned models in the rows above. However the only comparison that turns out to be statistically significant is that of RT-any (in row 3c versus row 4; p < 0.001) with the fine-tuned network being superior to the retrained model.
For anecdotal evidence on the behaviour of our different trained classifiers, we provide in Figure 8 the predictions of the different models for RB-any on a short example of a tabla solo segment with the ground truth annotated. We observe that the drum-pretrained model predictions actually cluster around the occurrences of the ground-truth tabla strokes even if they don’t clear the peak-picking threshold. The untrained model in this figure was a randomly initialised network and predicts onset probabilities concentrated around the value 0.5. We observe that the retrained and fine-tuned models make similar predictions for this example.
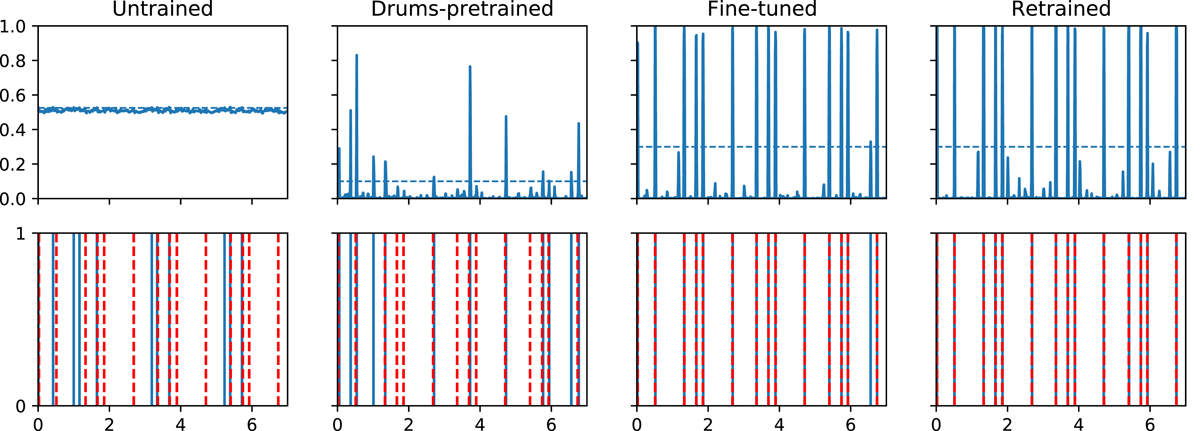
Figure 8
Automatic transcription for the RB-any in a short tabla solo segment. Top: model output activations versus time (horizontal dashed line is the peak-picking threshold); bottom: estimated onset locations (solid blue) and ground truth (dashed red). From left to right – untrained, drum-pretrained, tabla fine-tuned and tabla retrained models.
To confirm that drum-pretraining results in adequately trained models, we evaluate the ADT performance of the pretrained models on the IDMT test set (Table 7). Our results compare well with those of the CNN model of Southall et al. (2017a); the higher f-score obtained by our models could be due to our slightly larger training dataset. The table also shows the ADT test f-scores resulting from the use of additional drum data modification and augmentation during training. The modifications seem to benefit HH and KD classification more than SD, whereas in the case of tabla (Table 6), only the RB-any category seemed to benefit from them.
Table 7
ADT performance (test f-scores) on the IDMT-set comparing SOTA from ADT literature, against our models trained using different drum augmentation methods.
| METHOD | HH | SD | KD | MEAN |
|---|---|---|---|---|
| Southall et al 2017 (CNN) | – | – | – | 83.1 |
| Our models | 82.7 | 85.3 | 90.2 | 86.1 |
| + HH only | 80.2 | – | – | – |
| + RF aug | 84.5 | – | – | – |
| + SD-KD data repeat | – | 85.5 | 93.9 | – |
| + PS aug | – | 80.2 | 93.7 | – |
| + RS aug | – | 82.7 | 90.3 | – |
| + PS, RS aug | – | 81.1 | 90.6 | – |
6.2 Overall four-way classification
Individual classifiers corresponding to the atomic strokes D, RT-any and RB-any are combined to achieve the required 4-way tabla stroke classification as illustrated by Figure 2. We choose the sets represented by the following rows in Table 6: row 2 corresponding to the pretrained model, row 3 (taking the best of rows 3-3g for each stroke type) corresponding to the fine-tuned model and row 4 corresponding to the retrained model. Thus, for the fine-tuned system, we employ the HH-only and RF augmented version for D classifier, SD-KD repeat for RT-any and RB-any classifiers with drum pitch-shifting augmentation further included in the latter. For reference, we also present the performance of the 4-way classifier of the previous work (Rohit et al., 2021).
F-scores of the resulting 4-way classification system appear in Table 8. Apart from test set f-scores, we present the performance on CV (where the otherwise unseen-instrument validation fold is used only for early stopping of training and for tuning the peak-picking threshold for final onset detection). Given that the training data is drawn from tabla solo music and the test data from tabla accompaniment, this affords us the opportunity to observe performance within and across tabla playing styles. Statistical significance testing reveals that the CV f-scores of the retrained model are comparable to those of the fine-tuned model except for the case of the RT class where the fine-tuned model is superior (p = 0.002). All the other f-score differences observed between the corresponding columns of row 2 and 3 in Table 8 are found to be associated with significance value p > 0.05. For the test data performances, this arises from the relatively small size of the test set.
Table 8
Four-way CV/test classification f-scores for the transfer learning and retraining methods. The best set of D, RT-any, RB-any models combines the individual highest scoring D, RT-any and RB-any methods from the fine-tuned models of Table 6 (i.e. the values in bold in Table 6). Overall f-score is across the four categories. As expected from our understanding of transfer learning, all values in row 2 (fine-tuned model) are significantly higher than those in row 1 (p < 0.001). Values in bold are highest across rows 2 and 3. The asterisk marks the only significant difference (p = 0.002 in this case) between f-scores of corresponding fine-tuned and retrained models of this work (i.e. rows 2 and 3).
| METHOD | D | RT | RB | B | OVERALL | |
|---|---|---|---|---|---|---|
| 1 | Drum-pretrained | 57.8/44.0 | 40.9/48.7 | 16.2/17.5 | 3.6/2.1 | 44.8/36.2 |
| 2 | Best set of D, RT-any, RB-any models (Table 6) | 89.2/83.0 | 86.1*/86.0 | 73.2/63.6 | 89.2/81.5 | 86.7/81.2 |
| 3 | Retrained | 89.2/83.6 | 84.3/86.6 | 73.7/66.9 | 89.0/82.7 | 86.3/82.1 |
| 4 | Retrained Rohit et al. (2021) | 88.2/83.8 | 83.7/84.6 | 71.2/34.0 | 87.9/82.0 | 85.5/79.5 |
Finally, the category-wise best f-scores and the mean f-scores are higher (except for test set D) than the corresponding values reported by Rohit et al. (2021) for the same task with a very substantial improvement in RB f-scores, especially the RB test f-score. We reason that adding B strokes to the training data for RT-any and RB-any models potentially alleviates a limitation of the transfer learning approach of Rohit et al. (2021) using multi-label ADT models, where B strokes were not used during training. Our current system not only has increased training data for RT-any and RB-any models, but also matches better with the three target classes of the ADT task, as might be expected from the similarity of the main acoustic characteristics visualised in the spectrograms of Figure 4. With the least training data available for RB, the additional use of B onsets to train RB-any models in the new system has paid off well. At the same time, the classification of B strokes has also improved, pointing to the benefits of viewing atomic strokes as target classes and applying the co-occurrence neighbourhood to identify the compound stroke.
Across the stroke categories, we note that RB strokes are relatively poorly classified across the different systems. To understand this better, we analysed the model predictions on the test set to find that the main sources of error were missed detections due to faintly articulated RB strokes and false positives from damped strokes being misclassified as RB due to sustaining bass resonances from a previous stroke. We also uncovered some incorrect labelling of RB strokes as B due to similarly sustaining treble harmonics. Such errors, due to effects of overlap from decaying strokes, have been previously reported in tabla bol classification Chordia and Rae, 2008). Although the input context frames provided to the CNN model are aimed at overcoming such errors, it could be useful in the future to explore ways to provide more effective contextual cues such as an explicit language model. It is also interesting to note that RB strokes played in isolation are harder to detect accurately than those that co-occur with RT (as evidenced by the lower f-score for RB compared to B in Table 8). A possible explanation is that the stronger onset of RT strokes complements the weaker RB onset and facilitates detection of both onsets in B strokes.
7. Conclusions
We presented a system for classification of tabla strokes into a set of four musicologically defined categories. While the target use case is tabla accompaniment in vocal and instrumental concerts, the more easily available (but potentially mismatched) tabla solo data is used for training. Our chief contributions in this work comprised the investigation of a new approach to tabla stroke classification that facilitated leveraging Western drum datasets for transfer learning, and the investigation of training data augmentation methods for both drums and tabla that could help improve the performance of the four-category detection. The acoustic similarity with drums was exploited by viewing tabla strokes in terms of sound-production based atomic strokes, namely the resonant stroke on each of the treble and bass drums, and the damped stroke on either or both drums.
Compared to previous work consisting of four separate models, one for each category, our current system with the three atomic stroke models achieves a higher classification performance, especially for the more data-constrained resonant bass category, that can be attributed to the more diverse training data now available from resonant both strokes. This highlights the advantage of addressing the tabla stroke classification task via the reduced set of production-based atomic strokes as target classes.
The second important contribution is the investigation of the transfer learning paradigm, with Western drums and tabla treated as source and target domains respectively. We observe the expected gains in classification performance from drum-pretraining and subsequent tabla fine-tuning compared to an untrained model. However, the accuracy of the best fine-tuned model surpasses the corresponding retrained model only in one case – RT class in tabla solo CV. While this result points to limited benefits of our specific transfer learning approach, it is still encouraging given the number of distinct approaches to fine-tuning that have yet to be explored in the given context (Guo et al., 2019). Further improvements are expected from increases in the source training data size and diversity.
A hierarchical procedure starting with the four-way categorization could benefit the traditional tabla bol transcription task. Although the direct bol classification results of Gillet and Richard (2003) show fewer confusions across bols of different production categories, this performance is likely to be worse with larger and more diverse test sets and therefore stands to benefit from the methods of this paper. Future work will involve constructing a larger test set of annotated tabla accompaniment data and extending the classification to the context of tabla accompaniment audio extracted from vocal concerts, possibly aided by music source separation methods.
Data Accessibility Statement
The trained models and code are available for academic research use at this URL: https://github.com/DAP-Lab/4way-tabla-transcription.
Competing Interests
The authors have no competing interests to declare.
