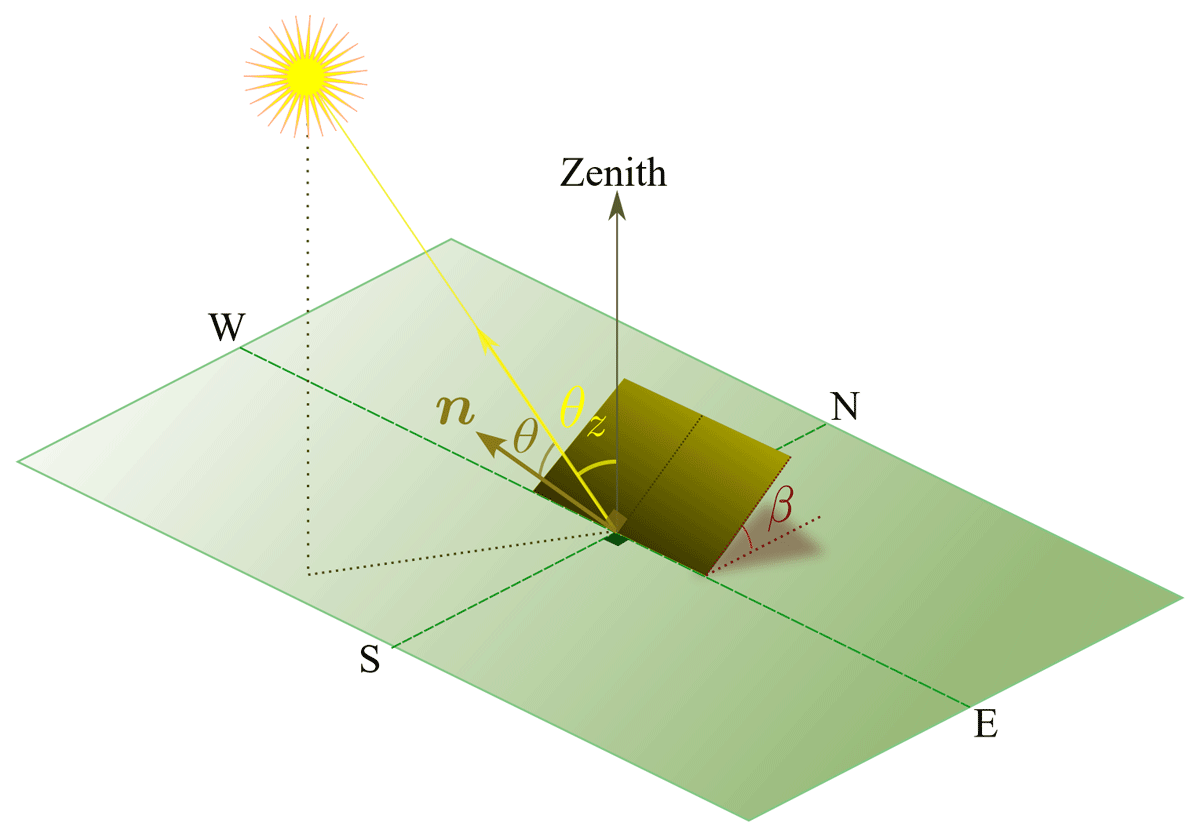
Figure 1
A flat solar panel is placed at a latitude ϕ, aligned along the North–South direction with a tilt angle β. The incidence angle θ is the angle between the Sun’s rays and the normal vector to the solar collector, n. The solar zenith angle θz is the angle between the Sun’s rays and the normal vector to the horizontal plane at the observation point.
Table 1
Comparison between pysolorie, pvlib-python, and astropy
| pysolorie | pvlib-python | astropy | |
|---|---|---|---|
| Use Case | Optimal tilt angle calculation for flat solar panels | Simulation of photovoltaic energy systems | Astronomy and astrophysics tools |
| Sun Tracking | No Sun Tracking (panel is fixed at optimal tilt angle) | Implements one-axis sun tracking, including backtracking and shading [213] | Not Supported |
| Optimization Target | Maximize beam energy via optimal fixed tilt | Minimize incidence angle with one-axis tracking | Not applicable |
| Astronomical Calculations | Basic solar position for energy modeling | Includes solar position, irradiance, and system modeling | Comprehensive celestial mechanics, coordinate systems, etc. |

Figure 2
Main components and their interactions for calculating the optimal orientation of solar panels.
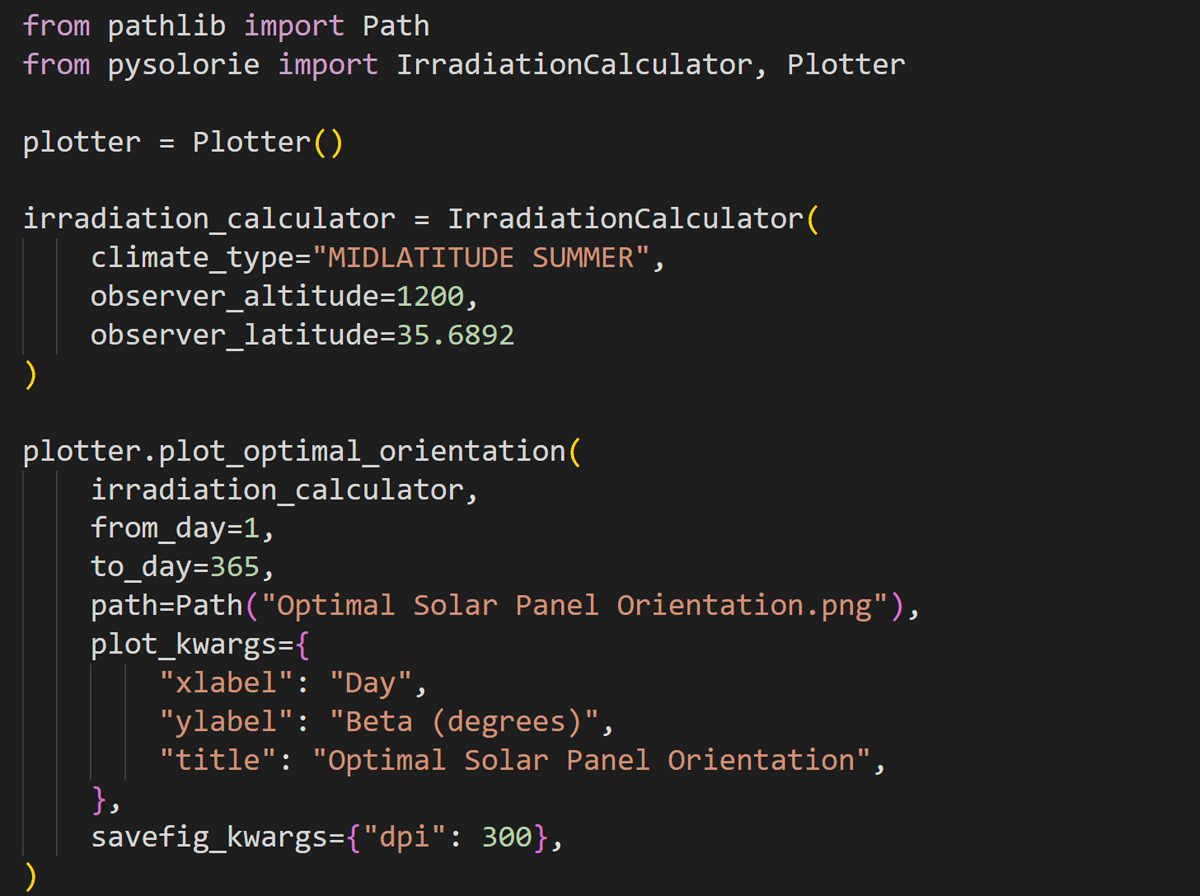
Figure 3
The code plots the optimal orientation for each day of the year for the city of Tehran.
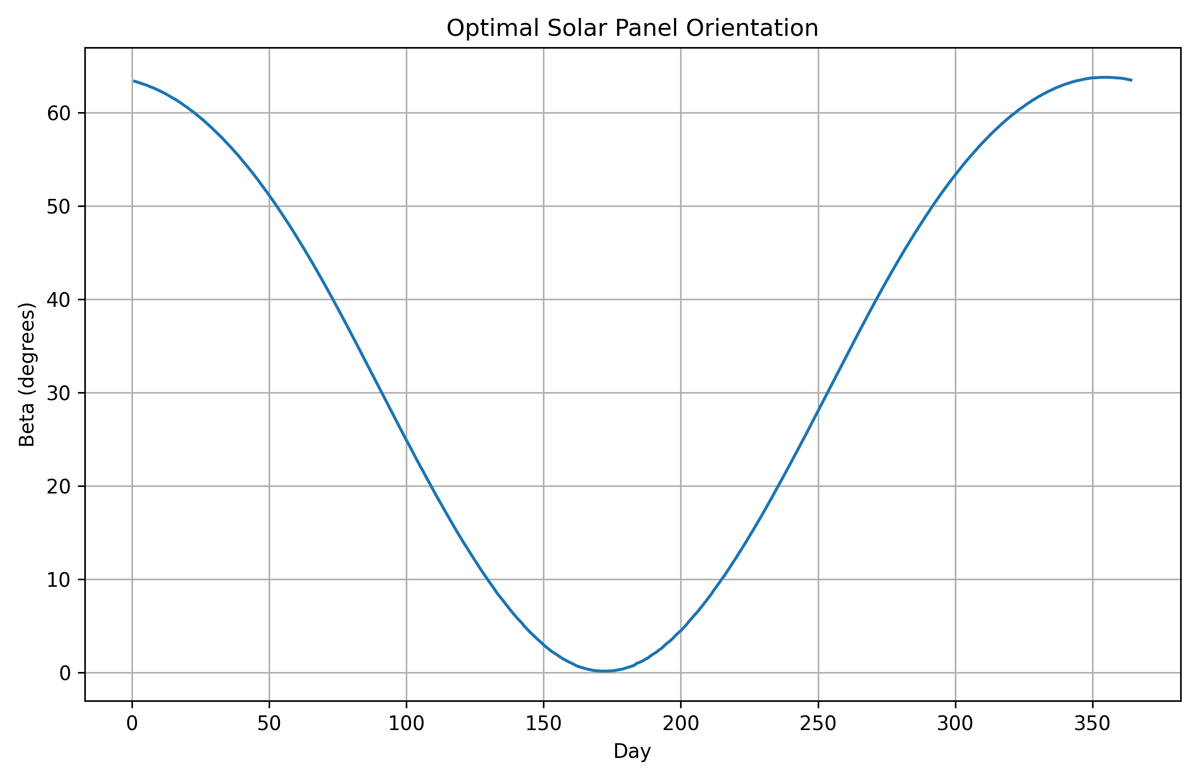
Figure 4
The optimal orientation of a solar panel for each day of the year in Tehran.
