Accurate sensor measurements are essential in modern measurement systems, yet sensor nonlinearity remains a significant challenge affecting overall accuracy. Several techniques can address this issue, but the use of a two-stage piecewise linear analog-to-digital converter (ADC) has proven highly effective for sensor linearization [1],[2],[3],[4],[5],[6],[7],[8],[9],[10]. By integrating sensor linearization and signal digitization into a single process, the mentioned ADC reduces processing time, power consumption and implementation costs, making it highly suitable for resource-constrained measurement applications. Because of these advantages, two-stage piecewise linear ADCs are widely used for the linearization of various sensor types, including NTC thermistors, Pt100 sensors, angular position sensors, and humidity sensors [1],[2],[3],[4],[5],[6],[7], [11].
Other sensor linearization techniques often suffer from limitations such as high memory and computational demands, particularly when the sensor's transfer function is unknown [12], [13]. Although neural networks have been explored as an alternative approach, their implementation requires large amounts of training data and significant computational resources [12], [14], [15]. In contrast, the two-stage piecewise linear ADC performs sensor linearization without these overheads, providing a more resource-efficient solution.
The traditional two-stage piecewise linear ADC architecture uses a separate ADC for each conversion stage. Linearization is performed in the first stage with a flash ADC whose transfer function approximates, in a piecewise linear manner, the inverse of the sensor's static transfer function. The input range of the flash ADC is divided into segments of varying widths (nonuniform segments), each bounded by specific points called break voltages. These break voltages are used as reference voltages for the comparators in the flash ADC. In the second conversion stage, a linear ADC is used, which may be implemented as a flash ADC or as another type, such as a successive approximation (SAR) ADC. Within the second conversion stage, each input voltage sample is further mapped to a uniform sub-segment within the corresponding nonuniform segment defined earlier. Although linearization is not performed in this stage, the subdivision improves both resolution and measurement accuracy. The resolutions of the first and second conversion stages are usually not equal. It is generally preferable for the first stage to have higher resolution, as sensor linearization primarily occurs at this stage. However, increasing the resolution of the first stage also increases implementation complexity.
An advantage of a two-stage piecewise linear ADC is its adaptability to different sensor types by adjusting the comparators' reference voltages in the flash ADC using a resistor ladder network. Given this advantage, reducing the complexity, power consumption, and implementation costs of the two-stage piecewise linear ADC remains an important research objective.
This paper presents a compact and cost-effective design for a two-stage piecewise linear ADC, in which both conversion stages are performed using a single flash ADC, with the addition of two comparators, one at the start of each conversion stage. This design strategy significantly reduces the overall comparator and resistor counts. Notably, in the proposed design, each additional comparator contributes one bit of resolution, unlike the traditional approach, where increasing the resolution of a conversion stage by one bit doubles the number of comparators.
This paper proposes a compact two-stage piecewise linear ADC designed to improve sensor linearity and increase measurement accuracy. The key contribution of the proposed design is a substantial reduction in component count compared to traditional architecture. Unlike traditional two-stage piecewise linear ADC implementation (see Fig. 1), the proposed approach achieves the same total resolution with significantly fewer comparators by reusing a single flash ADC for both conversion stages and incorporating only two additional comparators. Although several methods for increasing resolution with fewer comparators have been explored in the literature [5], [6], [16], the proposed design achieves greater compactness by further reducing the number of resistors required in the flash ADC's resistor ladder network [17], [18]. Since comparators are among the most power-consuming components in flash ADC circuits [19], reducing their number, as well as the number of resistors, decreases circuit complexity, power consumption and implementation costs. This makes the proposed design a highly efficient alternative to the traditional two-stage piecewise linear ADC design.
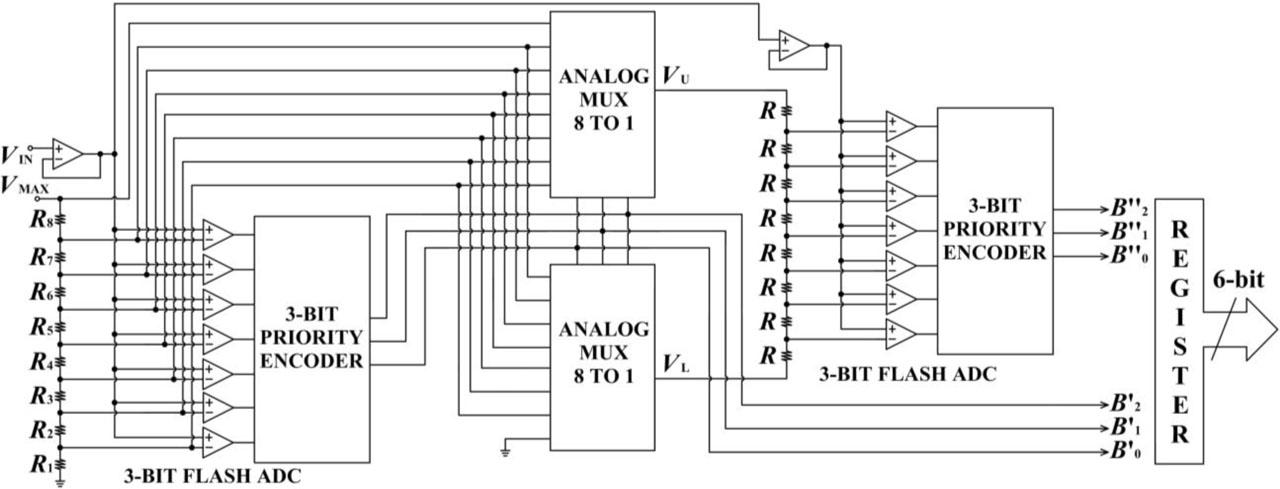
Traditional 6-bit two-stage piecewise linear ADC using a separate 3-bit flash ADC in each conversion stage.
Fig. 1 illustrates a traditional 6-bit two-stage piecewise linear ADC, where each conversion stage uses a separate flash ADC. It is well established that the implementation of an N-bit flash ADC requires 2N resistors and 2N−1 comparators [17], [18]. In the example shown in Fig. 1, two 3-bit flash ADCs are used, resulting in a total of 14 comparators (7 per stage) and 16 resistors across two independent resistor ladder networks. The input range of the first conversion stage spans from 0 V to VMAX (VMAX = f(xMAX), where f(x) is the sensor's transfer function and xMAX is the maximum value of the measured parameter x), and the current sample of the input voltage signal is denoted as VIN. In this example, both stages are configured with the same resolution; however, this configuration is not a requirement in practical implementations. Typically, the first stage is implemented with a lower resolution than the second due to the complexity of designing a nonuniform resistor ladder network (R1 to R8), which determines the reference voltages for the comparators. However, higher resolution in the first stage is desirable, as linearization is performed at that point.
The second stage is simpler to implement, using a uniform resistor ladder network composed of identical resistors R. This allows the use of uniform off-the-shelf ADCs in the second stage (e.g., flash, SAR, or other types) [1],[2],[3],[4], [6], [11], [20]. Equal resolutions of 3 bits per conversion stage were chosen in the traditional architecture, shown in Fig. 1, to enable a direct comparison with the compact 6-bit two-stage piecewise linear ADC proposed in this paper.
The proposed 6-bit architecture, shown in Fig. 2, differs fundamentally by replacing two 3-bit flash ADCs with a single 2-bit flash ADC and two additional comparators. Each of these comparators (C1 and C5) independently contributes one bit of resolution. Determining the nonuniform reference voltages of all comparators Vi in the first conversion stage, including the reference voltage VREF1 of the additional comparator C1 (see Fig. 2), is a critical aspect of the design. These voltages can be determined using the following equations:
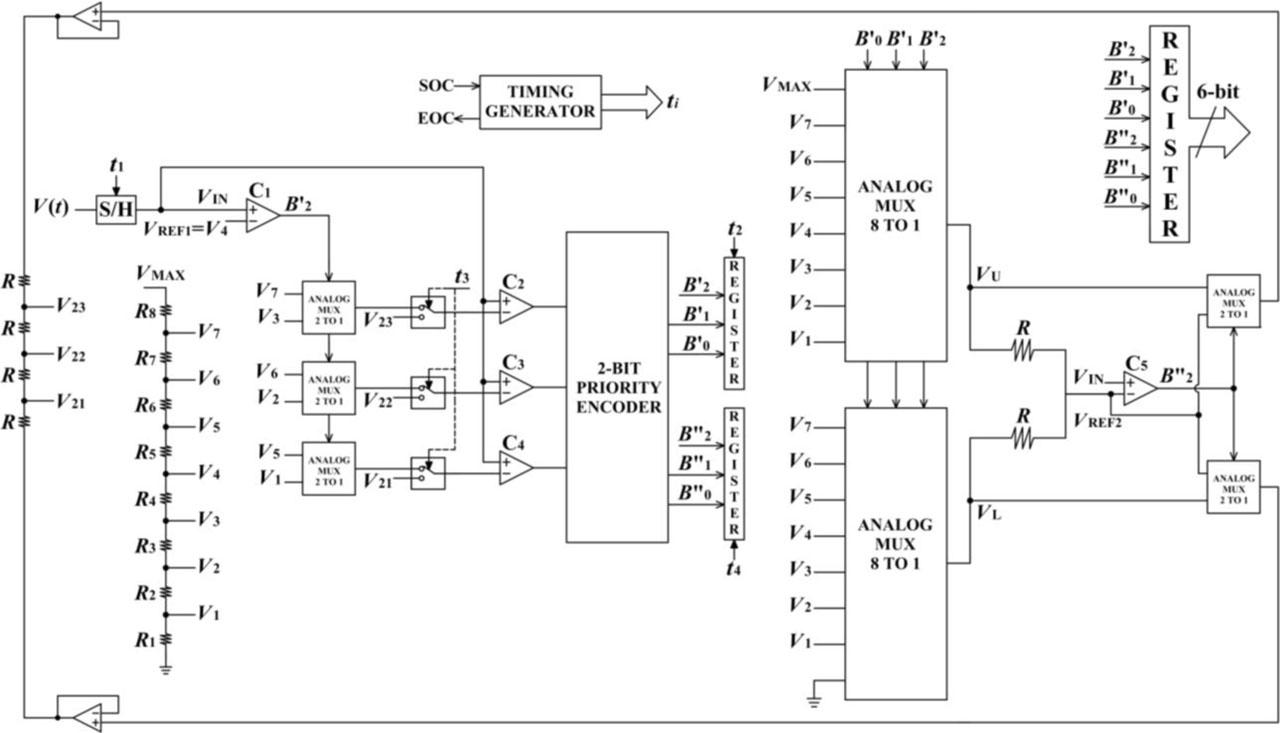
Compact 6-bit two-stage piecewise linear ADC using one 2-bit flash ADC and two additional comparators (C1 and C5).
The resistor values used to set these reference voltages are determined as follows:
In the proposed two-stage piecewise linear ADC (see Fig. 2), the initial step is to set the reference voltage VREF1 of comparator C1, which corresponds to the central reference voltage V4. The input sample VIN is captured at a moment determined by the timing generator signal t1. The sample is then routed to the input of comparator C1. Comparator C1 evaluates whether the input sample VIN is greater than or less than the voltage VREF1. If VIN > VREF1, the output bit B′2 = 1; otherwise, B′2 = 0. This bit controls three 2-to-1 analog multiplexers, which route either the reference voltages less than VREF1 or those greater than VREF1 to the inputs of the flash ADC comparators, depending on the value of VIN. As a result, the input range of the flash ADC is dynamically selected as either from 0 to VREF1 when B′2 = 0, or from VREF1 to VMAX when B′2 = 1. After selecting the relevant reference voltages and comparing them against VIN, a 3-bit code is generated and then converted into a 2-bit binary code by a priority encoder, producing the output bits B′1 and B′0. The combined bits B′2B′1B′0 represent the result of the coarse stage and are stored in the output register at the timing signal t2. These bits also control two 8-to-1 analog multiplexers, which select the corresponding lower VL and upper VU reference (break) voltages representing the boundaries of the nonuniform segment to which the input sample VIN belongs. Simultaneously, VL and VU define the input range for the second stage of conversion.
Similar to the first stage, the second stage starts with an additional comparator, C5, placed before the flash ADC. The reference voltage VREF2 of comparator C5 represents the midpoint between VL and VU, defined as:
This voltage is generated using two resistors of equal value R, forming a passive voltage divider as shown in Fig. 2. Comparator C5 then determines whether the input sample VIN lies above or below VREF2, producing the bit B″2. The output bit of comparator C5 controls the operation of two 2-to-1 analog multiplexers. These multiplexers dynamically define the input range of the same flash ADC used in the first conversion stage. When B″2 = 0, the input range of the flash ADC spans from VL (lower bound) to VREF2 (upper bound).
Conversely, when B″2 = 1, the input range shifts from VREF2 (lower bound) to VU (upper bound). In future work, the proposed two-stage piecewise linear ADC may be redesigned to eliminate comparator C5 and integrate its function into comparator C1, along with a circuit modification that enables switching the reference voltage between VREF1 and VREF2, resulting in a small reduction in conversion speed.
In the second conversion stage, the resistor ladder network consists of four equal-value resistors R instead of eight, since only three uniformly spaced reference voltages are required, compared to the seven nonuniform ones needed in the first stage. A network of switches, controlled by timing signal t3, selects the corresponding reference voltages: nonuniform reference voltages V1 to V7 for the first conversion stage, or uniform reference voltages V21, V22, and V23 for the second stage.
Fig. 3 illustrates the method for determining the break voltages of the nonuniform segments (V1 to V7) in the first conversion stage and the break voltages of the uniform sub-segments (V21, V22, and V23) in the second conversion stage. By dividing the sensor's input range, which spans from 0 to xMAX, into eight equal parts (for n = 3 bits) and mapping the boundaries of these divisions onto the corresponding values on the y-axis, the break voltages of the eight nonuniform segments are obtained. Each nonuniform segment is encoded with a corresponding 3-bit binary code ranging from 000 to 111. Depending on the input voltage sample VIN, one of these nonuniform segments serves as the input range for the second, uniform conversion stage (between VL and VU). The right side of Fig. 3 presents a detailed view explaining how the uniform break voltages V21, V22, and V23 are determined in the second conversion stage (for example, when VL = 0 V and VU = V1). In this case, the reference voltage VREF2 also influences the values of the break voltages for the uniform sub-segments, as it defines the input range for the flash ADC in the second stage. Each of these uniform sub-segments is also represented by a unique 3-bit code word, ranging from 000 to 111. The values of the break (reference) voltages V2j in the second conversion stage can be determined as follows:
1)
(6) \matrix{{{V_{{\rm{IN}}}} < {V_{{\rm{REF}}2}},} & {({{B''}_2} = 0)} \cr}, (7) \matrix{{{V_{2j}} = {V_{\rm{L}}} + j \cdot {{{V_{{\rm{REF}}2}} - {V_{\rm{L}}}} \over {{2^{n/2 - 1}}}},} & {j = 1,2, \ldots,{2^{n/2 - 1}} - 1} \cr}, or
2)
(8) \matrix{{{V_{{\rm{IN}}}} < {V_{{\rm{REF}}2}},} & {({{B''}_2} = 1)} \cr}, (9) \matrix{{{V_{2j}} = {V_{{\rm{REF}}2}} + j \cdot {{{V_{\rm{U}}} - {V_{{\rm{REF}}2}}} \over {{2^{n/2 - 1}}}},} & {j = 1,2, \ldots,{2^{n/2 - 1}} - 1} \cr}.
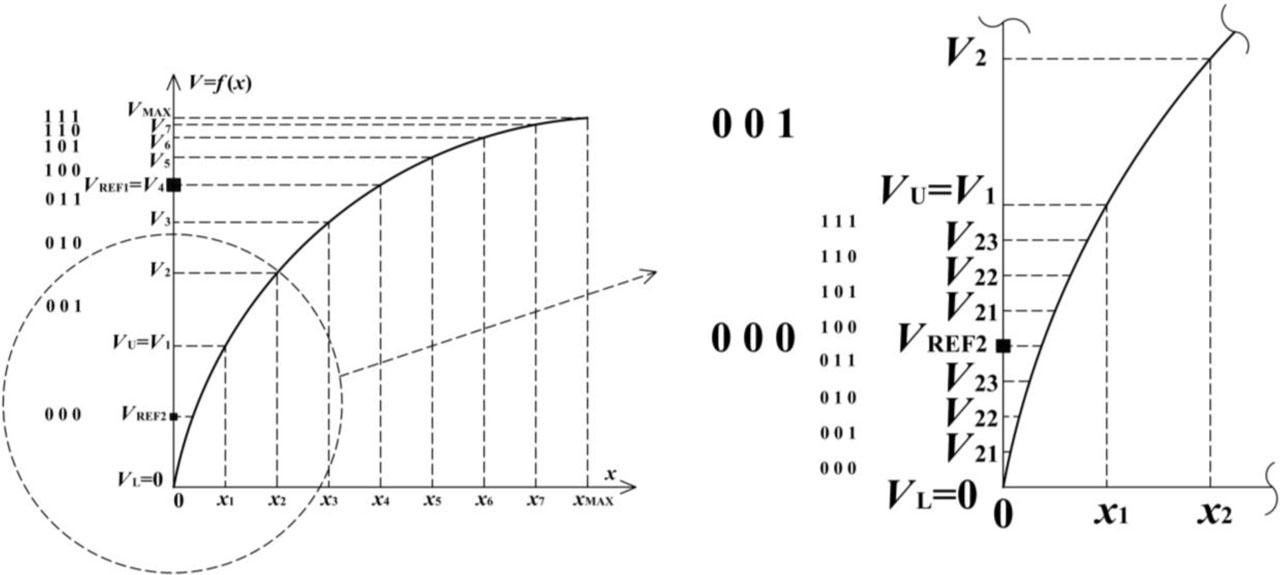
Illustration of a method for determining the break voltages of nonuniform segments (V1 to V7) in the first conversion stage and the break voltages of uniform sub-segments (V21, V22, and V23) in the second conversion stage (enlarged detail on the right).
Once the switches are closed under the control of timing signal t3, the new reference voltages V23, V22, and V21 are applied to the inputs of comparators C2, C3, and C4, respectively. This is followed by the conversion of a 3-bit code into a 2-bit binary code using a 2-bit priority encoder, which produces the final two bits of the digital output, B″1 and B″0. When the full 3-bit code B″2B″1B″0 is latched into the output register at the moment defined by timing signal t4, the conversion process is complete, resulting in a digital representation of the input voltage sample VIN.
It is important to emphasize that after converting the complete 6-bit code B′2B′1B′0B″2B″1B″0 back to an analog voltage, and consequently to the corresponding value of the measured parameter, a significantly smaller discrepancy can be expected between the actual and measured values [1],[2],[3],[4],[5],[6],[7]. In other words, the measurement error caused by the sensor's nonlinearity can be considerably reduced with the proposed linearization circuit.
This section provides a comparative analysis of how the resolution of a two-stage piecewise linear ADC affects the comparator and resistor requirements in both traditional and proposed compact designs. For the traditional two-stage piecewise linear ADC, the total number of comparators nct and resistors nrt can be determined using the following expressions [17], [18]:
Here, Nt = n/2 represents the resolution of each flash ADC in the traditional two-stage configuration, where n denotes the total resolution. Each addend in both expressions corresponds to one conversion stage.
In the proposed compact two-stage piecewise linear ADC design, the total number of employed comparators ncp is:
In this expression, the two addends with a value of 1 represent the additional comparators C1 and C5, while the addend (2Np−1) corresponds to the number of comparators used in the flash ADC with a resolution of Np = n/2−1. The total number of resistors used in the proposed compact design nrp is given by:
To assess the improvements introduced by the compact design compared to the traditional approach, the relative differences in comparator counts δc and resistor counts δr are computed as follows:
Table 1 presents key parameters for various total resolution values n, including flash ADC resolutions, Nt = n/2 for the traditional design and Np = n/2−1 for the proposed design. It also lists comparator and resistor counts for both architectures, along with their relative differences, highlighting the hardware savings of the proposed architecture.
Numerical values of key parameters for various total resolution values n.
| n | Nt | Np | nct | nrt | ncp | nrp | δc [%] | δr [%] |
|---|---|---|---|---|---|---|---|---|
| 6 | 3 | 2 | 14 | 16 | 5 | 14 | 64.2857 | 12.5000 |
| 8 | 4 | 3 | 30 | 32 | 9 | 26 | 70.0000 | 18.7500 |
| 10 | 5 | 4 | 62 | 64 | 17 | 50 | 72.5806 | 21.8750 |
| 12 | 6 | 5 | 126 | 128 | 33 | 98 | 73.8095 | 23.4375 |
| 14 | 7 | 6 | 254 | 256 | 65 | 194 | 74.4094 | 24.2187 |
| 16 | 8 | 7 | 510 | 512 | 129 | 386 | 74.7059 | 24.6094 |
| 18 | 9 | 8 | 1022 | 1024 | 257 | 770 | 74.8532 | 24.8047 |
| 20 | 10 | 9 | 2046 | 2048 | 513 | 1538 | 74.9267 | 24.9023 |
| 22 | 11 | 10 | 4094 | 4096 | 1025 | 3074 | 74.9634 | 24.9512 |
| 24 | 12 | 11 | 8190 | 8192 | 2049 | 6146 | 74.9817 | 24.9756 |
| 26 | 13 | 12 | 16382 | 16384 | 4097 | 12290 | 74.9908 | 24.9878 |
| 28 | 14 | 13 | 32766 | 32768 | 8193 | 24578 | 74.9954 | 24.9939 |
| 30 | 15 | 14 | 65534 | 65536 | 16385 | 49154 | 74.9977 | 24.9969 |
| 32 | 16 | 15 | 131070 | 131072 | 32769 | 98306 | 74.9989 | 24.9985 |
As the total resolution n increases, the difference in the number of comparators and resistors between the traditional and proposed two-stage piecewise linear ADC designs becomes more pronounced. As previously noted, Table 1 lists the total number of comparators nct and resistors nrt for the traditional design, along with the corresponding values for the proposed compact design ncp and nrp across various resolution values n. It also includes the calculated relative differences in comparator counts δc and resistor counts δr between the two designs.
The numerical results clearly demonstrate a significant reduction in hardware complexity achieved by the proposed design. As the total resolution n increases, the relative differences δc and δr grow steadily. Specifically, for resolutions exceeding 14 bits, both metrics show a strong upward trend, approaching their maximum values of 75 % and 25 %, respectively. These peak values will be fully attained when the total resolution reaches 42 bits. Even at lower resolutions n, the savings in component count are considerable, highlighting the cost-effectiveness of the proposed solution. This reduction translates directly into lower manufacturing costs, improved compactness, and reduced power consumption, making the proposed two-stage piecewise linear ADC highly suitable for sensor linearization in embedded or resource-constrained systems.
It should be noted that the introduction of comparators C1 and C5, together with additional multiplexers, causes a certain increase in conversion time. However, this is compensated by performing linearization and analog-to-digital conversion within a single circuit, which reduces the overall time required to process the sensor output signal, as well as the associated implementation cost.
This paper presents a novel compact two-stage piecewise linear ADC that improves sensor linearity while exhibiting reduced hardware complexity. By sharing a single flash ADC between both conversion stages and introducing two additional comparators, one for each stage, the proposed design achieves the same total resolution as the traditional design but with a substantially lower component count. Analytical expressions and numerical analysis show that the proposed architecture requires significantly fewer comparators and resistors than its traditional counterpart, with the savings becoming more pronounced as total resolution increases.
The numerical results validate the advantages of the proposed compact design. At higher total resolutions, the compact design achieves up to a 75 % reduction in comparator count and up to a 25 % reduction in resistor count compared to the traditional two-stage piecewise linear ADC with the same total resolution. These reductions directly lead to lower energy consumption, reduced silicon area, and decreased manufacturing costs. Even at low and moderate resolutions, the proposed design yields notable savings, confirming its suitability for compact, low-power embedded applications. Furthermore, by combining sensor linearization with digital conversion in a single process, the two-stage piecewise linear ADC delivers improved performance in modern smart sensing systems. Overall, the results confirm that the proposed compact two-stage piecewise linear ADC is a highly efficient, scalable, and cost-effective solution for high-resolution, low-power sensor linearization.