The fatigue life method can be used to certify metallic aircraft structures depending on the structure classification and/or aircraft certification regulations. However, the fatigue failure mechanism results in variability, or “scatter”, in experimental fatigue tests. This is because fatigue damage nucleates as a microstructural phenomenon, and no two specimens are the same at this scale. This is an aleatoric variability, it is irreducible, and is attributable to the inherent, or natural variability in the material microstructure. Fatigue testing standards and operating procedures exist to minimise all other variability arising from test specimen geometry and surface condition, with accurate and calibrated measurements, to best characterise material fatigue performance.
This paper describes a study to determine whether fatigue test life scatter is best characterised by a Weibull or lognormal statistical distribution for a high strength steel used for landing gear structures. It is a response to “Face 2” of Brot’s ICAF 2017 Plantema Memorial Lecture (Brot, 2017) and 2019 follow-up paper (Brot, 2019) with the question; “Weibull or Lognormal Distributions to Characterize Fatigue Life Scatter?”. This paper considers 3 datasets of repeated fatigue tests with the same constant amplitude fatigue load:
Schijve dataset 18 fatigue test results for 2024-T3 aluminium alloy
Brot dataset 86 fatigue test results for 2000 and 7000 series aluminium alloys
HBK dataset 371 fatigue test results for a high strength steel
The Schijve dataset (Schijve & Jacobs, 1955), shown in Table 1, are fatigue test results reported in 1955 for 18 flat sheet specimens of 2024-T3 aluminium alloy, 2.0 mm thick, unnotched, Kt = 1.15, tested in constant amplitude with Smax = 157 MPa and R-ratio = 0. Schijve reported the distribution of these fatigue test results using a lognormal distribution in (Schijve & Jacobs, 1955, figure 9.2), and a lognormal and 3-parameter Weibull distribution in (Schijve, 1992, figure 1b and 2b). The text of Schijve & Jacobs, (1955) and Schijve (1992) define the lognormal distribution as a normal distribution where the variable is defined in logarithmic terms. In this case, x = log(N), where N is the fatigue life expressed in number of cycles to separation failure. Schijve Fatigue and Structures of Materials (Chapter 12: Fatigue and Scatter) shows these fatigue test results with a lognormal distribution and a 3-parameter Weibull distribution in the same plot. This is reproduced in Figure 1a (Schijve, 2009, figure 12.3). Figure 1b shows a comparison of the reanalysis of these data for the purposes of this paper. These show that the results agree equally well with both distributions, and that the differences between the distributions are in the lower and upper tails of the distribution. Identifying the distribution that best fits the lower tail, where the probability of failure is low, is the most important. In Schijve (2009) states:
“The validation of the two distribution functions requires large test series. It is difficult to discriminate between the two distribution functions if the number of test data of nominally similar tests is small.”
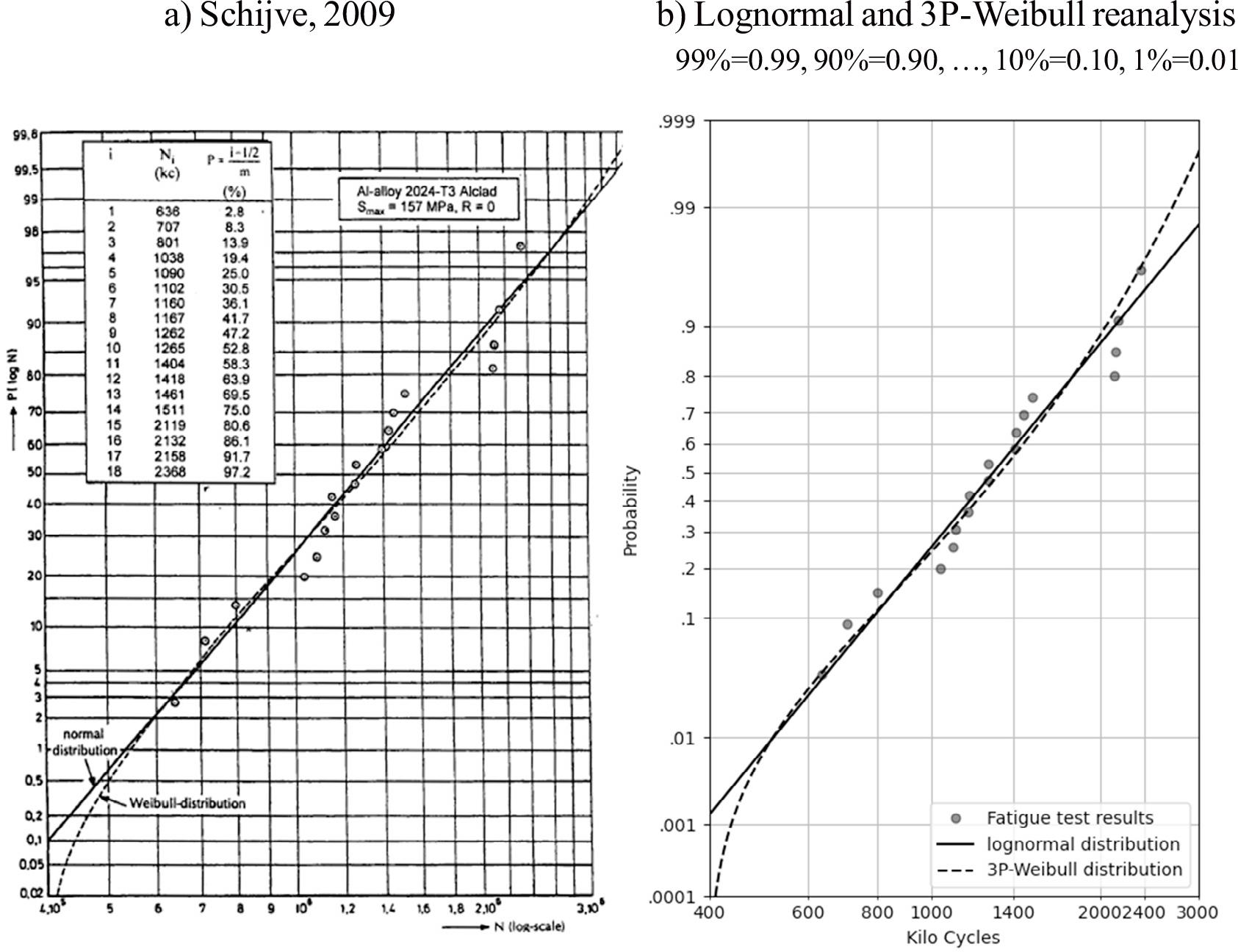
Lognormal and 3-parameter Weibull distribution of Schijve dataset fatigue test results a) reproduced from Schijve (2009, figure 12.3), and b) reanalysis for this paper.
Fatigue test results in Kilo Cycles (specimen number).
| 636 (13G) | 1160 (13J) | 1461 (12F) |
| 707 (13H) | 1167 (12H) | 1511 (13C) |
| 801 (13K) | 1262 (13A) | 2119 (12C) |
| 1038 (12K) | 1265 (13B) | 2132 (13D) |
| 1090 (13E) | 1404 (12G) | 2158 (12D) |
| 1102 (12J) | 1418 (13F) | 2368 (12E) |
Figure 1 shows similar distribution fitting, but does not attempt to replicate the exact distribution fitting. The vertical scale is calculated in such a way that the lognormal distribution becomes a straight line. Similarly a Weibull distribution plotted on a Weibull vertical axis becomes a straight line. A Weibull distribution plotted on a lognormal vertical axis will appear curved according to the distribution parameters. The cumulative density function (cdf) equations (1) to (4) for the distributions in Figure 1 are in Appendix A. Equations (1) and (2) for the cdf of a lognormal distribution show similar equations but differing between their base 10 and natural logarithms. These are the same, as any dataset that follows a lognormal distribution, will yield a normal distribution with any base logarithm. Equations (3) and (4) for cdf of a 3-parameter Weibull distribution, show their equations are the same. The small differences in cdf in Figure 1 are small differences in parameters from distribution fitting.
The distribution fitting parameters used in the reanalysis are:
Lognormal with Rank Regression on X, Median Rank, and Standard Ranking.
3-parameter Weibull with Maximum Likelihood, Kaplan-Meier, and Standard Ranking.
- ⚬
(The Kaplan-Meier estimator gave a closer match to the lower tail than Median Rank.)
- ⚬
Brot reanalysed the Schijve dataset in the ICAF 2017 Plantema Memorial Lecture “Three Faces of Aeronautical Fatigue - Face 2: Weibull or log-normal distributions to characterize fatigue life scatter: nearly identical twins or distant cousins?” (Brot, 2017) This compares Weibull and lognormal distributions for this dataset using SuperSMITH software developed by Fulton Findings. The method discussion states that Median Rank procedure is used for all Weibull and lognormal analyses in Brot (2017). Though not stated in the text, the figures show the distributions are 2-parameter Weibull as described in Abernethy “The New Weibull Handbook” (2006). Figures 2a and 3a reproduce these Weibull and lognormal distributions (Brot, 2017, figures 18 and 19), and Figure 2b and 3b shows reanalysis for this paper, with 95% confidence bounds added.

2-parameter Weibull distribution of Schijve dataset fatigue test results a) reproduced from Brot (2017, figure 18), and b) reanalysis for this paper.
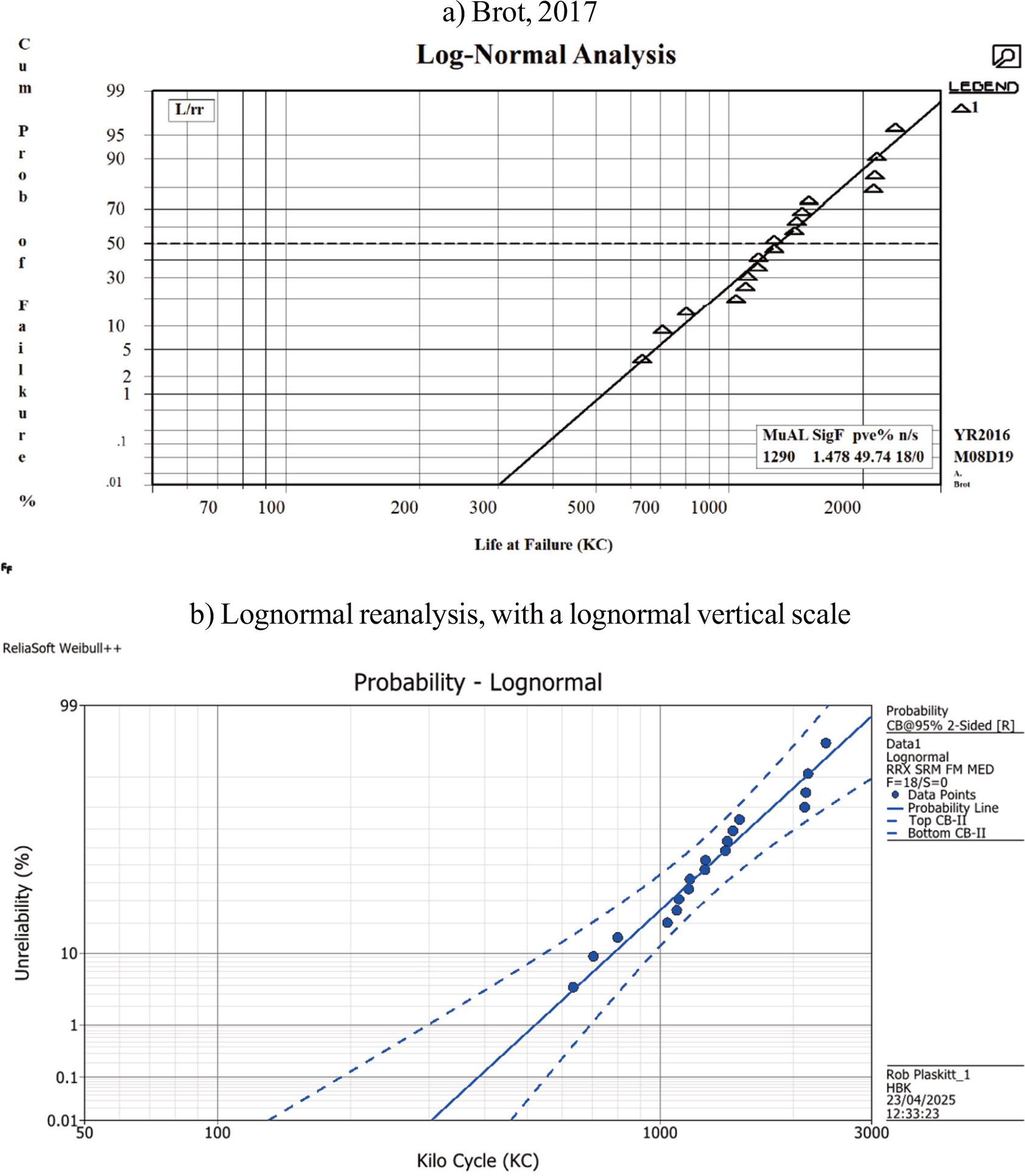
Lognormal distribution of Schijve dataset fatigue test results a) reproduced from Brot (2017, figure 19), and b) reanalysis for this paper.
Brot (2017) uses the extrapolated fatigue life at 0.01% probability of failure (=99.99% reliability) as a useful comparator between the Weibull and lognormal distributions, shown in Table 2.
Extrapolated fatigue life (Kilo Cycles) at probability of failure at 0.01% (=99.99% reliability).
| Distribution | Figure 2a distribution fit | Figure 2b distribution fit |
|---|---|---|
| Weibull | 86 | 86.3 |
| Lognormal | 300 | 303.4 |
Figures 2 and 3 demonstrate analysis consistency by repeating these analyses using ReliaSoft software (2024) developed by Hottinger Brüel & Kjær. The 2-parameter Weibull distribution equations (5) and (6) are in Appendix A.
The distribution fitting parameters used in the reanalysis are:
Lognormal with Rank Regression on X, Median Rank, Standard Ranking, and Fisher Matrix confidence bounds.
2-parameter Weibull with Maximum Likelihood, Median Rank, Standard Ranking, and Fisher Matrix confidence bounds
Brot (2017) continues discussion of this Schijve dataset and notes:
“Figures 18–26 all show that there are very sizable differences between the Weibull and Log-Normal distributions in setting allowable lives to minimize the probability of failure. In all cases, the Weibull results are much more conservative than the Log-Normal results.”
“However, from these results it is impossible to say which distribution is the more accurate. In actuality, the true result could be to the left of the Weibull result, between the Weibull result and the Log-Normal result or even to the right of the Log-Normal result.”
This 2nd bullet quote echoes Schijve’s statement that it is difficult to discriminate between the two distribution functions with this dataset, with limited fatigue test results in the lower tail. Again, identifying the distribution that best fits this lower tail, where the probability of failure is low and is most important, is not possible with this dataset.
Brot [1] continues discussion with comments on different approaches between Boeing and Airbus:
“Boeing developed the methodology to determine fatigue life variability of safe-life structures using the Weibull distribution.”
- ⚬
Earlier text specifies this as a 2-parameter Weibull distribution by referencing Boeing Company technical reports (Whittaker & Besuner, 1969; Whittaker, 1972) and Int. J. Fatigue paper (Goranson, 1997).
- ⚬
“On the other hand, it was reported that the Log-Normal distribution is used extensively by Airbus for fatigue life variability analyses.”
… and concludes by proposing:
“A sixty-specimen fatigue test program was proposed by the author in order to better evaluate the fit of the Weibull and Log-Normal distributions to actual fatigue test data.”
Following reanalysis of the Schijve dataset it is useful to compare the 3-parameter Weibull distribution used to reproduce Schijve’s analysis in Figure 1, with the 2-parameter Weibull distribution used to reproduce Brot’s analysis in Figure 2. These are compared in Figure 4, where a) is a copy from Figure 1, and b) combines the lognormal and 2-parameter Weibull distributions from Figure 2b and 3b onto the same lognormal y-axis scale in an image with similar size and aspect ratio.
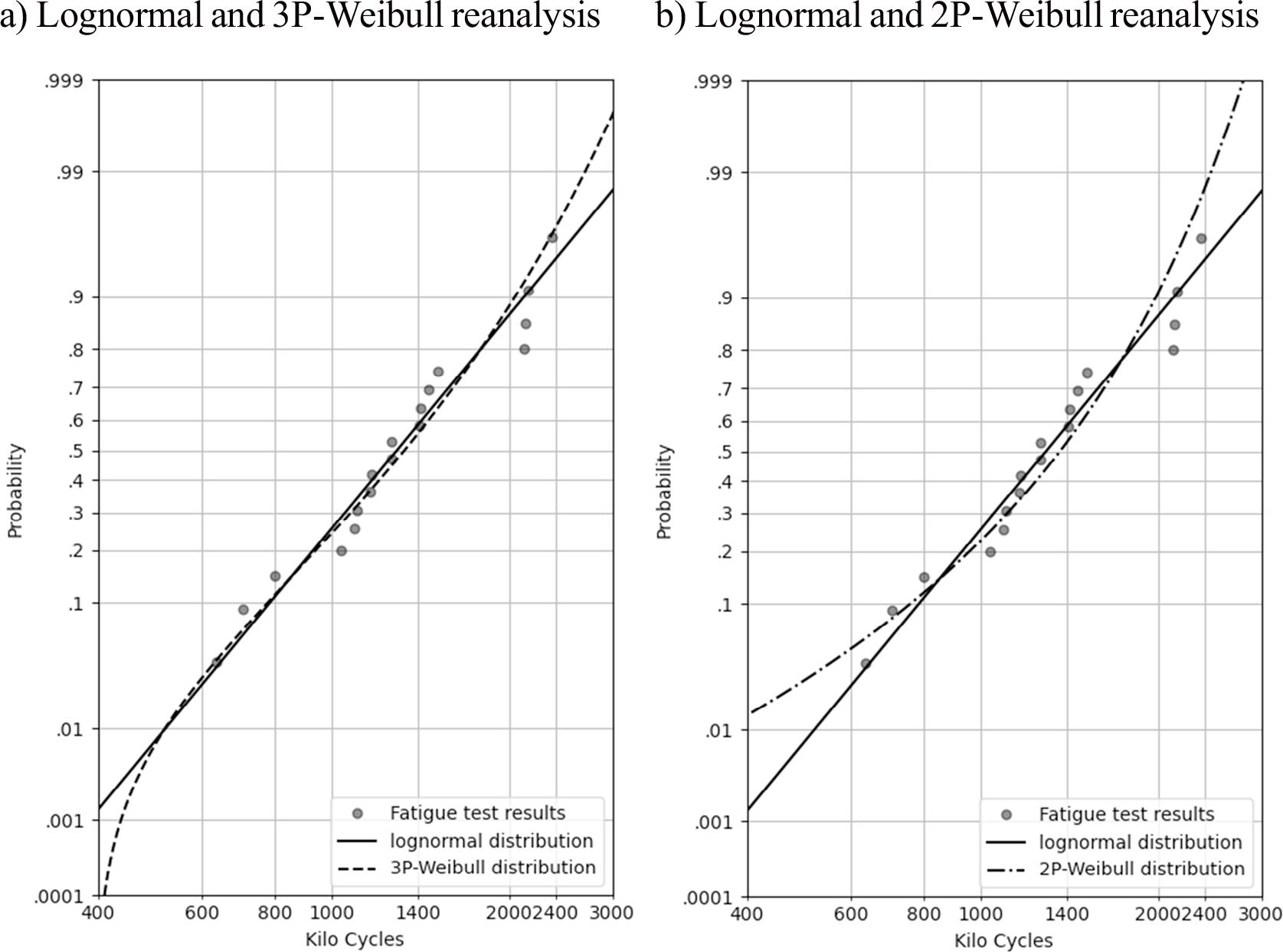
Lognormal and Weibull distribution of Schijve dataset fatigue test results a) with 3-parameter Weibull as used in Schijve analysis (2009), and b) with 2-parameter Weibull as used in Brot analysis in (2017).
This highlights the difference between a 2- and 3-parameter Weibull distribution in the lower tail. The additional parameter is the location parameter γ (gamma), the failure free life. When γ (gamma) = 0 the 3-parameter Weibull equation (2) reduces to the 2-parameter Weibull equation (4). A 3-parameter Weibull trends towards a positive failure free life calculated from the dataset whilst a 2-parameter Weibull always trends to zero.
Abernethy (2006) “3.5 Curved Weibulls and the t0 Correction” uses t0 for location parameter and identifies a physical criterion that should be met before using 3-parameter Weibull:
“There should be a physical explanation of why failures cannot occur before t0. For example, bearings cannot spall instantaneously. Many rotations are required to produce the damage.”
All fatigue tests to separation or load drop failure meet this criterion for a 3-parameter Weibull distribution, where the failure free life, the location parameter, must be greater than zero because some load cycles are always required. Failure at zero cycles is a tensile test, a strength failure, not a fatigue test. Failure at a small number of cycles is considered to be a gross deformation or plasticity failure rather than a fatigue failure. The Schijve dataset are from unnotched specimens with “experiments continued until failure” (Schijve & Jacobs, 1955) failure criteria. This is assumed to be until separation.
However in Goranson (1997) states that the Boeing Company selected a 2-parameter Weibull distribution for structural life distribution:
“The two-parameter Weibull distribution is used for the structural life distribution mode. In this application structural life is defined as the operational life to initiation of a fatigue crack of detectable size. The Weibull distribution was selected after considerable USAF-sponsored research in the late 1960s and early 1970s. Furthermore, the two-parameter model was chosen to recognize the conservative possibility of a detectable fatigue crack being present at zero life.”
From the references in (Goranson, 1997) the USAF sponsored research in the late 1960s and early 1970s is the Whittaker reports (Whittaker & Besuner, 1969; Whittaker, 1972). They are the only references for those dates. These reports use non-homogenous datasets including fatigue test specimens with open holes, edge notched, pin connected and riveted spotweld, bolted and bonded joints and combination joints. In this context, where failure is defined by the presence of a fatigue crack of detectable size, there could be a detectable crack at zero life in the joint specimens.
Both Abernethy and Goranson statements are correct in their context. Their choice of 2- or 3-parameter Weibull depends on the fatigue tests conducted and the failure criteria they use.
It is useful to conclude this discussion of reanalysis of the Schijve dataset with a demonstration of how fatigue test results can be used for statistical analysis without revealing their number of cycles to failure. Conducting fatigue tests is expensive, time consuming, requires special test equipment, and experienced personnel. Consequently many fatigue test datasets are confidential.
The failure free life calculated from a 3-parameter Weibull distribution, the location parameter γ (gamma), can be used to normalize the number of cycles at a probability of failure. Table 3 shows how 3-parameter Weibull trends towards a failure free life at the Weibull location parameter γ (gamma), for a range of probabilities of failure. Conversely lognormal and 2-parameter Weibull continue extrapolating to the lower limit of their distributions at zero cycles to failure. Table 4 shows how the failure free life γ (gamma) can be used to normalize these.
Extrapolated fatigue life (Kilo Cycles) at probability of failure (reliability).
| % Probability of failure (% reliability) | Lognormal | 2-parameter Weibull | 3-parameter Weibull γ (gamma) = 503.4 |
|---|---|---|---|
| 1% (99%) | 521.7 | 363.8 | 582.5 |
| 0.1% (99.9%) | 387.5 | 177.1 | 525.7 |
| 0.01% (99.99%) | 303.4 | 86.3 | 509.7 |
| 0.001% (99.999%) | 245.3 | 42.1 | 505.2 |
| 0.0001% (99.9999%) | 202.8 | 20.5 | 503.9 |
Extrapolated fatigue life normalised to γ(gamma) at probability of failure (reliability).
| % Probability of failure (% reliability) | Lognormal | 2-parameter Weibull | 3-parameter Weibull |
|---|---|---|---|
| 1% (99%) | 1.036 | 0.723 | 1.157 |
| 0.1% (99.9%) | 0.770 | 0.352 | 1.044 |
| 0.01% (99.99%) | 0.603 | 0.171 | 1.013 |
| 0.001% (99.999%) | 0.487 | 0.084 | 1.004 |
| 0.0001% (99.9999%) | 0.403 | 0.041 | 1.001 |
The Brot dataset is described in “Weibull or Log-Normal Distribution to Characterize Fatigue Life Scatter – Which is More Suitable?” (Brot, 2019). This ICAF 2019 paper followed the ICAF 2017 proposal for a sixty-specimen fatigue test program, and the introduction comments:
“Unfortunately, the author did not have the facilities or budget to perform this test program. Over the last two years, no other organization has volunteered to perform this test program. Therefore, the author has formulated an alternate method to try to solve this problem, which is described below.”
It is not possible to reanalyse this dataset because it is confidential and the number of cycles to failure are not known. However it is useful to describe this dataset to understand the approach used and its similarity with previous work.
The Brot dataset is 86 fatigue test results from a combination of 2000 series and 7000 series aluminium alloys, combined from the following four sources.
Schijve dataset of 14 unnotched flat sheet 2024-T3 aluminium alloy, after eliminating the 4 highest life specimens (>2,000,000 cycles, specimens 12C, 13D, 12D and 12E).
Israel Aerospace Industries, 10 fatigue specimens manufactured from 7075-T73 aluminium alloy with holes. (No further details in the public domain.)
Various test results donated by industrial contacts. (No details in the public domain.)
Several S-N results from MMPDS version 9, 2014. (The results selected are not known.)
For the majority of these 86 fatigue test results their number of cycles to failure is either not known or not in the public domain. This dataset includes multiple materials, from multiple sources, for notched and unnotched specimens, and with their number of cycles to failure combined and normalised:
“… combined and normalized to result in a "Characteristic Life" of 50,000 cycles for the entire database. (This had no effect on either the Weibull or Log-Normal calculated parameters.)”
This is a non-homogenous dataset, when compared with the homogenous Schijve dataset of a single material in a single specimen configuration with repeated fatigue tests in the same load conditions.
This approach to combine multiple non-homogeneous fatigue test results into a single dataset is similar to that followed by Boeing Company technical reports [9, 10 Whittaker]. These considered 3 material categories (aluminium, steel and titanium) with each including fatigue test results from specimens with open holes, edge notched, pin connected and riveted spotweld, bolted and bonded joints and combination joints.
Brot (2019) uses this dataset to determine the Weibull and lognormal distribution and concludes that:
“It was determined, by this procedure, that the Weibull distribution appears to be much more suitable than the Log-Normal distribution for predicting the allowable service life of an aluminium structure to a specific probability of failure.”
The ideas for this paper arose from conversations and email correspondence with Brot following this ICAF 2019 presentation, and led to the authors reviewing their historical fatigue tests to search for a suitable dataset — the HBK dataset.
The authors work for Hottinger Bruel & Kjaer Ltd (HBK) in the United Kingdom (previously nCode International, at the time of fatigue testing), a company with more than 40 years history and experience conducting commercial stress-life and strain-life fatigue testing and supplying fatigue calculation software. They reviewed their historical fatigue tests to find the homogeneous dataset described below:
371 fatigue test results in 14 different batches with the number in each batch between 5 and 50.
All test specimens of the same “nominal” high strength steel material, commonly used for landing gear structures, with the same surface treatment condition.
All cylindrical test specimens with the same or very similar geometry and gauge length surface preparation.
All fatigue tests conducted in load control with the same R-ratio with load level to give the same maximum stress within ±1%.
All fatigue tests conducted by the same personnel in the same laboratory using annually calibrated servo-hydraulic test rigs, load cells and controllers.
All fatigue tests conducted between 2000 and 2010.
The resulting HBK dataset is large and homogeneous, and confidential. Permission has been generously and anonymously given to use these fatigue test results for the statistical analyses in this paper.
Figure 5 shows lognormal and 2- and 3-parameter Weibull distributions for this HBK dataset. This shows the 2-parameter Weibull trending towards zero, the 3-parameter Weibull trending towards a failure free life, with lognormal between them. All three distribution methods have a high correlation coefficient 0.99, 0.94 and 0.96 respectively, where 1.0 is a perfect fit. All fit these data well between 10% and 90% probability of failure, between 0.1 and 0.9 in the figure, though none are perfect with all data points on the fitted distribution line. The lognormal and 3-parameter Weibull distributions fit the lower tail much better than 2-parameter Weibull. This is highlighted in Figure 6 where the lower half of each distribution, between 0.01% and 50% (0.0001 and 0.5) are shown with 95% confidence bounds.
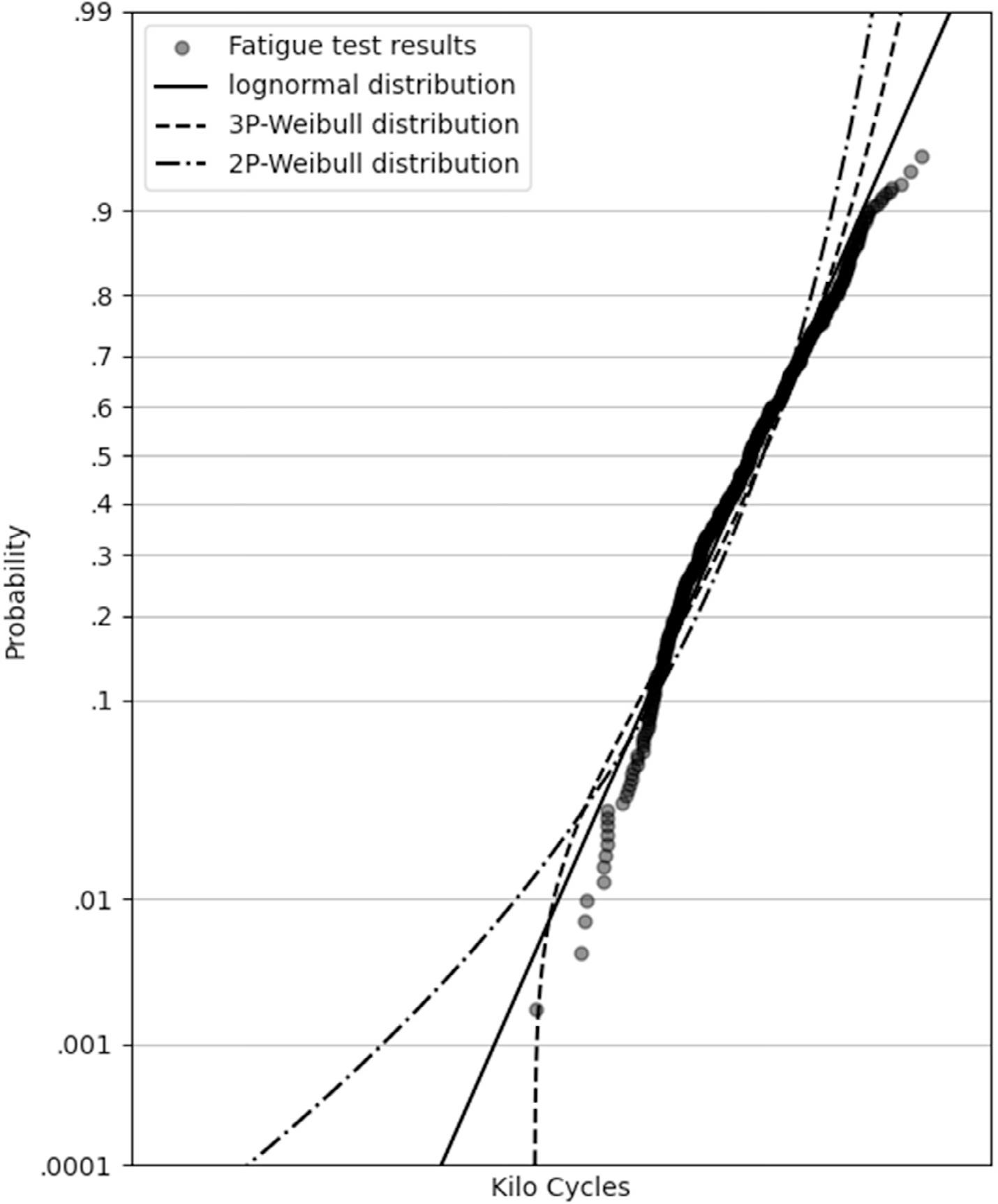
Lognormal and 2- and 3-parameter Weibull distributions of HBK dataset (logarithmic x-axis with numbers excluded to maintain data confidentiality).

Lognormal and 2- and 3-parameter Weibull distributions of HBK dataset with confidence bounds for the lower tail of the distributions between 0.01% and 50% (logarithmic x-axis with numbers excluded to maintain data confidentiality).
Table 5 shows a range of probabilities to failure for the fitted distribution normalized by the 3-parameter Weibull failure free life γ (gamma).
Extrapolated fatigue life normalised to γ (gamma) at probability of failure (reliability).
| % Probability of failure (% reliability) | Lognormal | 2-parameter Weibull | 3-parameter Weibull |
|---|---|---|---|
| 1% (99%) | 1.383 | 0.786 | 1.293 |
| 0.1% (99.9%) | 0.584 | 0.130 | 1.029 |
| 0.01% (99.99%) | 0.288 | 0.022 | 1.003 |
| 0.001% (99.999%) | 0.155 | 0.004 | 1.000 |
| 0.0001% (99.9999%) | 0.089 | 0.001 | 1.000 |
For this dataset Figures 5 and 6, and Table 5, show that it is better to use either lognormal or 3-parameter Weibull to determine an allowable life for a low probability of failure. The fitted lognormal distribution is recommended, or if an additional safety factor is desired, by its lognormal lower confidence bound. The 3-parameter Weibull is not recommended because it is too dependent on the lowest number of cycles to failure of all the specimens tested. The lognormal distribution allows a desired probability of failure (or reliability) to be chosen, and the distribution will extrapolate to the allowable life value. The 3-parameter Weibull distribution does not allow this because it converges to the failure free life γ (gamma). More fatigue tests will always have an increased probability of a test result with a lower number of cycles to failure. The 3-parameter Weibull distribution cannot predict this. The 2-parameter Weibull distribution is unpreferred because below 1% probability of failure it rapidly trends towards zero cycles with no fatigue test results in this region to support the lower tail of this distribution.
A large homogenous fatigue test dataset like this can be used for many statistical analyses, beyond the scope of this paper. This dataset contains tests from multiple batches with a wide range of number of specimens in each batch, enabling analysis to ensure batch to batch consistency of material supply, and/or different material suppliers. For example, this dataset has a ratio of about 200:1 between a specimen with the highest number of cycles, a runout, where the test was stopped with no separation failure, to a specimen with the lowest number of cycles to failure. Fatigue test results from one batch of tests occupied 8 out of the 10 longest lives, but still had 1 fatigue test result within the 10 shortest lives.
The Schijve dataset of 18 homogenous fatigue tests reported in 1955 has been reanalysed and compared with Schijve’s statistical distribution analyses (Schijve & Jacobs, 1955; Schijve, 1992; Schijve, 2009) and Brot’s reanalysis for ICAF 2017 Plantema lecture (2017). This demonstrates the difference between their analyses, with a 3-parameter Weibull analysis used by Schijve and a 2-parameter Weibull analysis by Brot.
Both Schijve and Brot concluded that this Schijve dataset consisted of insufficient fatigue test results to determine whether the distribution of fatigue life scatter is best represented by a Weibull or lognormal distribution.
Brot concluded the ICAF 2017 Plantema lecture (2017) with a call for “a 60 specimen fatigue test program in order to better evaluate the fit of the Weibull and Log-Normal distributions to actual fatigue test data”.
Brot introduced the ICAF 2019 paper (2019) stating that “the author did not have the facilities or budget to perform this test program” and “over the last two years, no other organization has volunteered to perform this test program” so presented an alternate method to try to solve this problem with a non-homogenous dataset of 86 fatigue test results. This concluded “…that the (2-parameter) Weibull distribution appears to be much more suitable than the Log-Normal distribution for predicting the allowable service life of an aluminium structure to a specific probability of failure”.
HBK* review of historical fatigue tests identified a homogeneous dataset of 371 constant amplitude cylindrical specimen fatigue tests from 14 different batches, conducted between 2000 and 2010, for a high strength steel used for landing gear structures.
Comparison of lognormal and Weibull distributions concluded that the HBK dataset fatigue life scatter is best characterized by the fitted lognormal distribution, or if an additional safety factor is desired, by its lognormal lower confidence bound.
- a.
The 2-parameter Weibull distribution is unpreferred for fitting fatigue life scatter because the 2-parameter Weibull distribution assumes failure starts from zero. This is not appropriate for fatigue tests where failure is the number of cycles to separation failure. Failure at zero cycles is a strength failure (a tensile test), and failure at a small number of cycles is a gross deformation or plasticity failure.
- b.
The 3-parameter Weibull distribution is unpreferred for fitting fatigue life scatter because at low probability of failure (high reliability) the distribution converges to the 3rd parameter, the failure free life, at the Weibull location parameter γ (gamma). More fatigue tests will always have an increased probability of a test result with a lower number of cycles to failure. The 3-parameter Weibull distribution cannot predict this.
- a.