The development of measurement systems enables monitoring of changes occurring in the space typical for civil engineering with any level of detail. A special case is monitoring of the construction site, particularly in real time [1]. Current control of the status of resources allows for their effective management.
Real-time updating of digital terrain model (DTM) is a valuable feature on a construction site. DTM is a digital, three-dimensional representation of terrain (ground) surface and objects for a given location and area. It can be used to represent the shape of terrain surface, calculate the height H of any point (on its surface) where XY coordinates are known, and determine values derived from the shape. This is because a DTM can also provide information about inclination and other topographic (characteristic) features of terrain, such as edges or faults. Moreover, the possibility of using DTM in software for designing in the BIM (building information modelling) technology seems particularly interesting [2].
The technologies used to acquire and update DTM include: InSAR (interferometric synthetic aperture radar), aerial photogrammetry, UAVs (unmanned aerial vehicles) and LiDAR (light detection and ranging) [3–5]. An efficient way of acquiring point clouds for DTM creation is provided by measurement platforms known as mobile mapping systems (MMS). In order to acquire point clouds and georeference them, a mobile vehicle is equipped with a number of devices such as: laser scanners, cameras, GNSS (global navigation satellite system) receivers, IMU (inertial measurement unit) sensors, odometers, and radars [6–8]. Their effective operation requires a multi-sensor fusion system to determine the position and orientation of a moving platform, based on Kalman filtering, among other things [9]. However, for obtaining data for machine control systems, data integration based on timestamps may be a sufficient solution [10,11].
Changes in the terrain surface caused by various factors require updating of DTM. Gagula et al. [12] provide an example of DTM for flood modeling. To update information about the object, they use a UAV positioned by RTK (real time kinematic) GNSS, supported by static GNSS measurement. In this case, the DTM was updated by UAV, in SfM (structure from motion) technology, not in real-time, not by LiDAR, but by photogrammetry. A similar study is presented by Ćwiąkała et al. [13], but it covers the use of UAV to acquire terrain deformations due to underground mining. As a result, they determine the accuracy of displacements in relation to the ground sample distance (GSD). Another solution is presented by Skaloud et al. [14], who deal with moving platforms for point cloud generation in real-time from ALS (airborne laser scanning) missions. They state that sub-decimeter accuracy is achievable and sufficient for many applications. Going further, Ernst et al. [15] present the use of a laser scanner to build a DTM of the surrounding environment to support the navigation of a multi-sensor system implemented using GNSS and IMU. The research found that laser scanning observations improve the results obtained by IMU+GNSS positioning. On the other hand, Koch & Lacroix [16] address the topic of managing environmental models within teams or robots. These devices are equipped with LiDAR sensors, providing point clouds that are used to incrementally build DTMs. Another example is given by Wang et al. [17], who present a fusion of LiDAR and IMU to develop terrain mapping for emergency rescue vehicles. In their work, they analyzed measurement errors and their impact on the accuracy of the vehicle localization, which amounted to 4–8 cm. Many of the solutions listed are designed for the extemporary needs, and data acquisition and processing are time-consuming tasks. However, a large part of the needs for providing geometric information about the surrounding terrain requires real-time operation. These include, in particular, mobile robots operating mainly on the basis of RGB-D cameras [18], off-road all-terrain vehicles [19], and wheeled planetary rovers [20], in which the model is updated thanks to the motion of the measuring platform. Another example of a real-time change detection system is presented by Ding et al. [21], who study the deformations of tunnel segments based on multi-sensor data fusion.
Providing real-time terrain data is also crucial for the operation of earthworks machines. Furthermore, systems providing real-time data must take into account the operating conditions of the system, especially in dusty environments [22]. Devices such as UAV and TLS can provide high-quality data on the current condition of the terrain. Robertson [23] notes, however, that the ability to generate data on a working machine means that it can respond to such deviations in real time. This translates into higher quality data, which in turn facilitates the management of mine resources and improves decision making.
Terrain modeling in the field of earthworks is a much broader topic, especially in the field of construction machinery automation. Multi-sensor systems are developed for mining shovels [24], bulldozers [25] and excavators [26]. Chae et al. [27] present the results of work on the construction of an autonomous earthwork system, in which laser scanning was used. The scanner collecting data was placed on a moving platform, and the registration of scans was carried out based on targets. The goal was to create a model of the actual earthwork environment. In turn, Guan et al. [28] develop a system for terrain mapping and navigation for excavator operations. The system acquires a 3D point cloud from the LiDAR, an RGB data from the camera, and the orientation of the excavator acquired from GNSS RTK. The created system allows for automatic navigation of the excavator in a real environment, in which there are stockpiles, hills and deep pits.
Most control systems are based on a static DTM provided by the surveyor on site, which, however, is not continuously updated. In currently used machine control/guidance systems, terrain measurement can only be performed manually by the operator, using the machine’s bucket/blade. At present, this feature is used mainly to create work surfaces for the system in the field, and for rough as-built measurements. It is provided by the main manufacturers of machine control systems, including Leica Geosystems AG [29], Trimble CE&C Help: Machine Control [30], Unicontrol ApS [31], Makin AS [32], Novatron Oy [33].
Some of these also have the so-called surface logging. If the function is enabled, places currently being cut by the blade are mapped. The result of the mapping can then be used by the operator or manager in the office (via file synchronization) to assess the progress of the work. Such possibilities are offered by software providers: AEC Software Technology [34], Trimble Construction Support [35], Leica Geosystems AG [36], Unicontrol ApS [37], Topcon Positioning Systems [38], Makin’ 3D Machine Control [39].
Manual logging of points by the user greatly limits the efficiency of DTM creation. Automated logging of points from the machine blade, on the other hand, does not provide fully accurate DTM results. This applies especially to areas where material is added. It is also not possible to perform initial mapping of the terrain (a pass before starting excavation, e.g. in order to create a precise cut/fill analysis) without physically modifying it.
The systems mentioned, even the advanced ones, which allow for semantic segmentation of objects occurring on the working site, are not designed with the current update of DTM in mind. An attempt to create a solution that focuses on probabilistic height determination was undertaken by Bhandari et al. [40]. In their solution, which allows for terrain mapping for mining shovels, 3D lidar sensors allow adding new observations to the existing terrain height map, taking into account false observations coming from, for example, dust on the measurement site. Their main achievement is the quick and effective update of dynamic changes to provide real-time terrain map. A similar solution, but much more extensively presented, is proposed by D’Adamo [41]. It uses a LiDAR sensor mounted on the machine and a set of RTK GNSS and IMU to position the moving platform. Among the many challenges indicated, the key is to provide real-time terrain maps based on a set of measuring devices, ultimately for the construction of fully autonomous bulldozers.
In this article, we propose a solution that provides the controlled machine with a DTM that is adequately prepared and updated in real time. An increasing number of studies in the field of real-time DTM updating for earthworks [40, 41] indicates a large potential for the development of the proposed system. Compared to the existing solutions, we propose several novelties:
Placing the system at the back of the construction machine, which allows for collecting data on the terrain after the drive and obtaining the current state of the terrain. This is important because after the bulldozer pass, the terrain cannot be expected to be perfectly flat due to the continuous track used in the vehicle propulsion. In addition, the current DTM is important for the planned optimization of the machine’s movement shaping the terrain in accordance with the design.
The measurement results are immediately oriented in the global coordinate system, and the nodes in the grid can have any values. The original measurement accuracy is also preserved by saving the exact XYZ coordinates of the last measurement in a specific cell. In the Bhandari solution [40], the height ranges (0.25 m) for a specific cell were predefined, leading to a decreased accuracy of the generated model.
No need for initial data to be available. Unlike in the D’Adamo proposal [41], which requires a reference surface (acquired e.g. by a UAV), no initial data is needed except the approximate size of the project, which can change freely in the course of the work anyway.
Improved LiDAR sensor performance (15 Hz instead of 10 Hz) while using a computer with a similar setup.
Discussion on the height grid. In particular, we indicate the dependence of the height grid on the driving speed, taking into account the hardware limitations of the measuring system.
A ready-made solution for the real-time DTM updating in the commonly used Python language. The presented approach involves planning and execution of both software and a physical implementation (prototype) for the problem described above.
In addition, it should be noted that in the experiment performed so far, D’Adamo [41] ultimately did not finish testing the algorithm with LiDAR due to sensor failure and used terrain prediction based on a model of the blade and tracks of the dozer. This data may be of limited accuracy due to the large number of variables.
By presenting the results of our research, we make a significant contribution to faster development of technology in construction by increasing the popularity of algorithms which update DEM in real-time. This is a significant deficiency that occurs even in professional, commercial machine control systems.
The remainder of this paper is arranged as follows. The equipment used for the study is presented in Section 2, along with the measurement setup. An explanation of the algorithm for data acquisition is presented in Section 3. The subject of Section 4 is the results of the field verification of system operation. They form the basis for the discussion presented in Section 5, and the final conclusions are given in Section 6. Additionally, the key functions used for the calculations are included in Appendix A in the form of Python code.
In order to answer the research question, a technical design of a prototype measuring platform for a bulldozer, and the principle for the sensors fusion on the platform were developed. The measuring platform was built to test the algorithm, which was developed to update DTM in real-time. Finally, an analysis of input parameters for the algorithm to operate was carried out.
The proposed measurement system is to be mounted on construction machines such as bulldozers, excavators and loaders. The proposed arrangement of the main system components (GNSS receivers, IMU and LiDAR sensor) is shown in Fig. 1. The figure also shows the area measured by the LiDAR sensor Velodyne VLP-16, which was used for the testing. When projected on a vertical plane, it logs 16 beams with a total angle of ±15° with respect to the horizontal plane of the sensor (Fig. 2a). For a standard size dozer such as the Caterpillar D6, the LiDAR would be mounted at a height of about 3 m. After setting the appropriate tilt of the sensor relative to the ground/dozer plane (about 45°) and narrowing down the data set in the sensor’s horizontal plane to ±35°, and distance measurement to 6 m, the obtained coverage of the measurement area just behind the machine will be entirely sufficient. This is because the whole set generates an area on the ground shaped roughly like a ring segment, the span of which is about 4.4 m on the inner side (just behind the machine), up to 6.8 m on the outer side (Fig. 2b), whereas the width of a standard dozer blade is around 3 m to 4 m. This provides adequate overlap to allow for a change of machine direction or material spillage outside the plough/bucket. These parameters are the starting point requirements for the testing of the measurement platform.

Visualization of an illustrative CAT D6R dozer with a Velodyne VLP-16 LiDAR sensor and a measurement beam with the Hz angle of ±35°, V angle of ±15°, and measurement range of up to 6 m
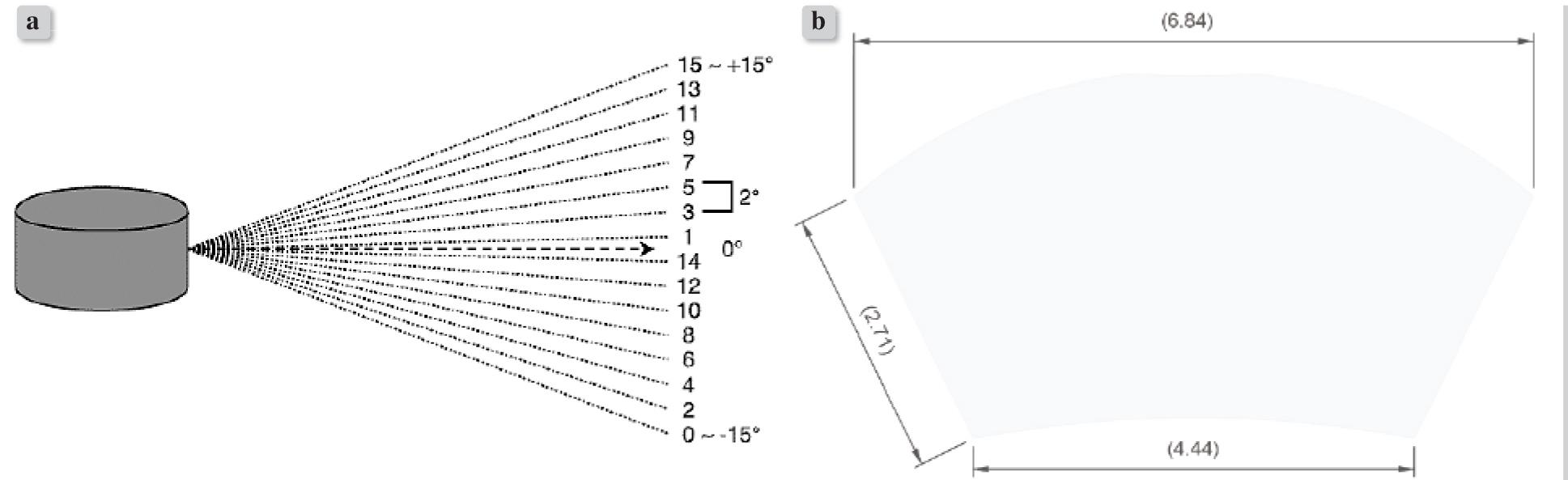
Velodyne VLP-16 LiDAR parameters: a) measurement beams (channels) in the vertical plane [42], b) dimensions of the measurement area [m]
To facilitate testing of the proposed algorithms, a portable measurement platform has been built. The heart of the prototype measurement system is the previously mentioned Velodyne VLP-16 rotating LiDAR sensor. The measurement platform is complemented by two GNSS RTK receivers, an IMU, Windows 11 tablet, frame made of aluminium profiles, 3D FDM printed mounts and adapters, as well as minor accessories and equipment for efficient power supply and data transmission. The whole set is shown in the photograph below (Fig. 3). The only modification compared to the previously mentioned setup of the measurement platform is raising the LiDAR sensor measurement angle in the horizontal plane from ±35° to ±90°, in order to streamline manual measurements in the field by increasing the measurement area and, additionally, burdening the algorithm with more incoming data. Visualizations of the portable platform with the discussed increased measurement angle are shown in Fig. 4.

Prototype of the measurement system
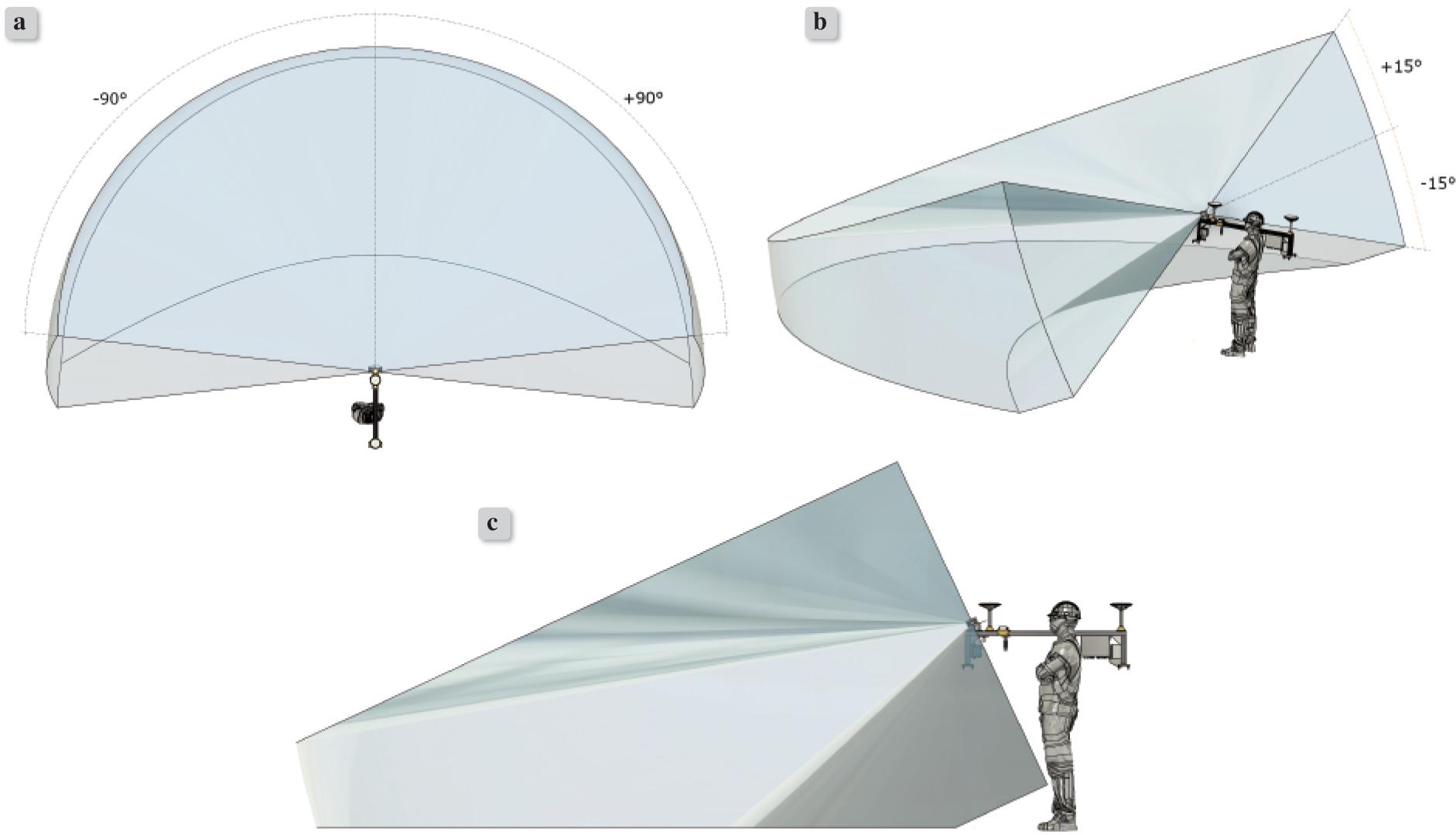
Visualization of the prototype with the LiDAR sensor measurement angle used in the tests: Hz ±90°, V ±15°, and measurement range up to 6 m: a) top view, b) spatial view, c) side view
The following section presents in more detail the proposed algorithm for real-time DTM updating. It was used in the prototype of the measurement system described above (Fig. 3). The software of the measurement system prototype was designed with five key functionalities in mind:
definition of the work area and initialization of the measurement data collection space,
acquisition of measurement data to create a DTM using a laser scanner (LiDAR Velodyne VLP-16), two GNSS receivers and an IMU sensor,
filtration and georeferencing of measurement data in the global coordinate system,
collecting and updating the DTM with specified parameters in real time using a computing unit with average parameters (Microsoft Surface Pro 9 tablet with Windows 11),
performing additional calculations based on the DTM in parallel (e.g. volume of earth mass, data visualization, saving data copies to file) using the same computing unit.
The diagram of the program based on the developed algorithm is shown in Figure 5, where the functionalities described above are also indicated.
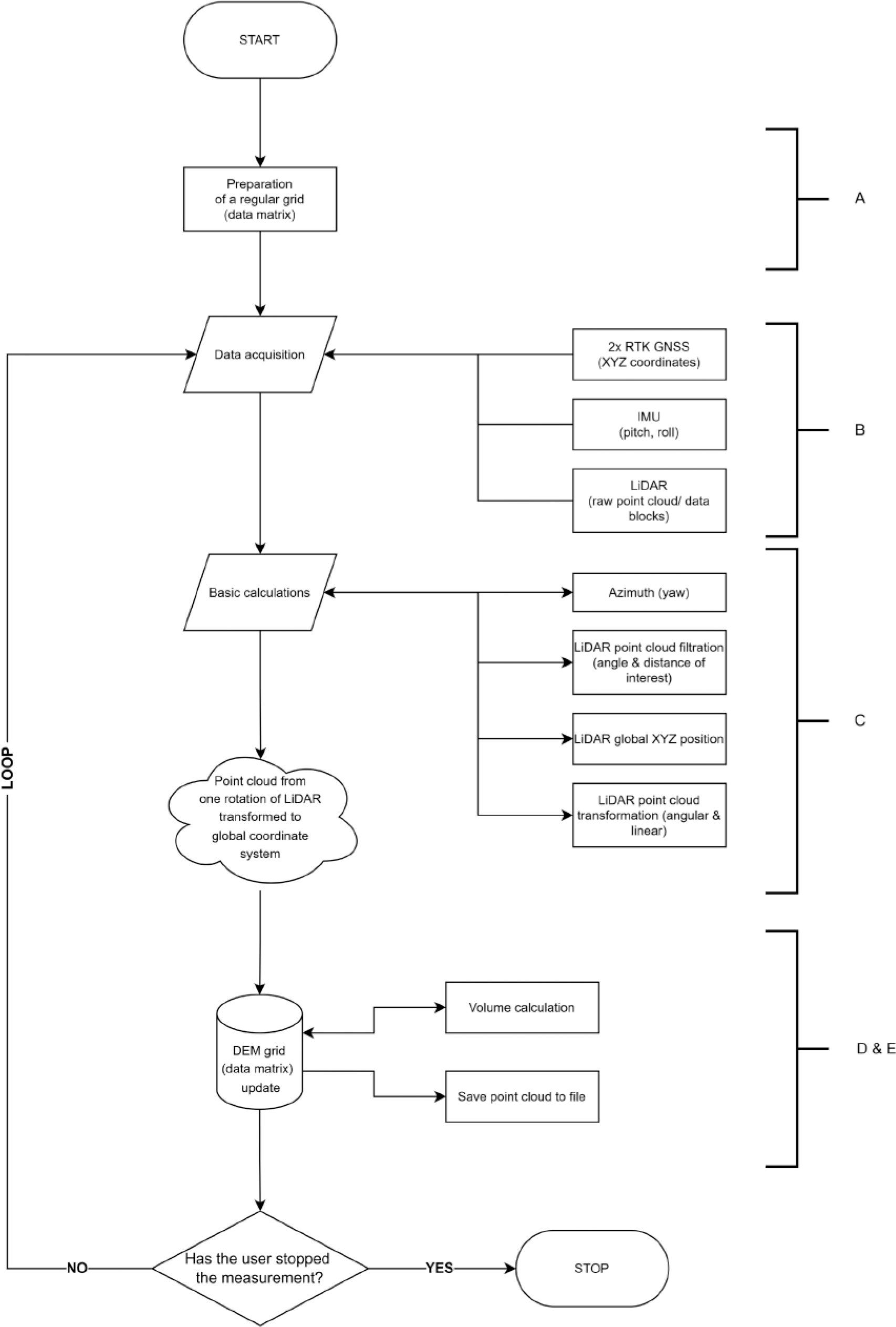
Block diagram of the program based on the developed algorithm
Functionality D has become an important optimization issue from the perspective of the time efficiency. It should be noted that, due to the geometric arrangement, the acquired LiDAR data are characterized by a significant mutual irregularity of the measured points based on which the DTM is created. In a single LiDAR measurement, the distances between points are variable on both the horizontal and vertical plane. In addition, given the system (platform) movement factor, it is not possible to obtain mutually correlated data in terms of position for a quick and unambiguous update of the Z height value at the same points. Additionally, smooth operation of the entire system is crucial for the process of creating and updating a DTM in real time and performing derivative calculations, such as material volume (part E). Therefore, selection of a method of data representation has a very strong impact on the ultimate operation of the algorithm. According to the analysis performed by D’Adamo [41] in Chapter 2, reducing the collected LiDAR data to a regular grid is the optimal approach.
The work on our software has shown that pre-occupying space in the program’s cache before starting the process significantly speeds up its subsequent iterations. Hence, before the start of LiDAR data recording and the DTM update process an empty data matrix is created (part A). It has a regular grid mesh size, and is expressed in the local coordinate system. Its length and width approximately cover the area for which the DTM will be updated (the software is designed to automatically increase the size of the data matrix in the event of exceeding the originally assumed measurement area).
The script performing the initialization of the data matrix is included in Appendix A as Code 1.
The elements of the data matrix A correspond to fragments of the terrain and are treated as “pixels” of a given size. The global coordinates X, Y, Z and other data describing a point physically measured in the terrain (LiDAR signal reflection intensity (Intensity), height difference to the design plane (Hdiff)) are recorded in subsequent “pixels”. The size of rows, and cols of the data matrix is described by the following relationship:
rows – the number of grid nodes (‘pixels’) on the X axis (rows), rows ∈ ℕ+,
cols – the number of grid nodes (‘pixels’) on the Y axis (rows), cols ∈ ℕ+,
L – the length of the DTM acquisition area on the X axis [m], L ∈ ℕ+,
W – the length of the DTM acquisition area on the Y axis [m], W∈ ℕ+,
px – the size of a grid node (“pixel”) [cm], a factor of 100, px {1,2,4,5,10,20,25,50,100}.
When data matrix Ai,j (i ∈ {0 ‥rows-1},j ∈{0 ‥cols-1}) is initialized, all vector items located at the grid nodes (“pixels”) are filled with zero values.
After the data storage space is prepared, the data acquisition and processing stage (part B) begins. The starting point for the measurement and computational part of the algorithm’s work is the point cloud from a single rotation of the LiDAR sensor, limited to an angle in the horizontal plane indicated by the user. For our platform, it was the angle of ±90° from the azimuth axis (Hz) of the device frame, as mentioned in the previous section. The key element is the orientation of the acquired clouds from subsequent rotations of the LIDAR sensor in the global coordinate system. This is achieved by determining the current position of the measurement system from GNSS and IMU observations. Part B was executed, among other things, through the application of serial communication (GNSS and IMU sensors) and Ethernet (LiDAR sensor), as well as the “pyubx2”, “pySerial” and “socket” libraries. Basic calculations (part C) were based on the “SciPy” library which calculates rotation using Euler angles [43].
In order to link the data matrix to global coordinates acquired through LiDAR (GNSS), translation parameters along the X and Y axes must be determined in order to obtain the minimum global coordinates Xmin, Ymin of the DTM acquisition area (part C). This is done by recording the global coordinates of the LiDAR sensor at the time of starting data acquisition (initial position Xinit, Yinit) and accounting for the size of the DTM acquisition area. The shift of coordinates measured by the LiDAR sensor relative to the data matrix is described by the following equation:
⌊·⌋ – means the floor function.
The main loop of the developed program covers continuous collection and integration of data from all sensors. The result of its single iteration is a point cloud from one rotation of the LiDAR sensor, limited to the selected angle. The point cloud is unorganized and randomly distributed geometrically, but oriented in the global coordinate system. This means that one area can have an overrepresentation and another a deficiency of data relative to a grid mesh of the DTM created and updated in real time. For this reason, the application of the integral part of the real number (floor function) in equation (3) is a very desirable procedure and an original optimization approach in the process of determining the position of a data matrix node. Only one point of the cloud can be recorded in that node.
The node index [rown, coln] of the data matrix at which the values will be replaced with ones coming from the nth point of the cloud from the measurement cycle is determined based on the following relationship:
n – point number in the point cloud collected during the measurement cycle,
Xn, Yn, Zn – coordinates of the nth point of an acquired point cloud.
In a specific node, all subsequent points belonging to that node are continuously replaced from the point cloud collected in a measurement cycle, which means that the finally saved change is the last one. This method of operation is justified by the fact that the algorithm operates independently of the measurement parameters – a change of the mesh size does not require a change of the algorithm.
Since it takes the same time to check whether a mesh node has data assigned to it from a previous measurement as to overwrite that node with new data, multiple data updates for mesh nodes do not delay the program's operation. In addition, this approach always provides the most up-to-date data, regardless of whether it was obtained from subsequent LiDAR rotations at insignificant fraction-of-a-second intervals or after a significant change in the shape of the terrain due to earthworks.
The script executing the update of the main data matrix is presented in Appendix A as Code 2. In addition to exact coordinates of the measured point X, Y, Z, also recorded are LiDAR beam reflection Intensity and the height difference between the height of the point and the design plane Hdiff, determined by the following formula:
Hproj – the height of the design plane (given by the user) at point X,Y.
A visualization of data matrix filling is shown in Figure 6.

Visualization of the data matrix – a grid with a single pixel size of px. Each pixel, starting in the lower left corner, can only contain one point with data [X,Y,Z, Intensity, Hdiff]. The colors blue, green and yellow indicate the corresponding grid nodes (pixels) and measured points
If the calculated index of the data matrix node rown or coln exceeds the maximum size of rows, or cols, a new row or column is added, depending on in which direction there is no space. Additionally, where the data matrix needs to be shifted in the negative direction, such shift should be taken into account by also recalculating Xmin and Ymin accordingly.
Having an always-up-to-date point cloud (in a DTM grid model), the volume of material (cut/fill parameters), among other things, can be continuously controlled. Height measurements can be referenced to a “0” level, a fixed horizontal plane, an inclined plane or a 3D model:
In the first case, volume calculation comes down to summing up the height column and multiplying it by the grid pixel area:
5 where:V = \sum\nolimits_{i = 0}^{rows - 1} {\sum\nolimits_{j = 0}^{cols - 1} {{Z_{i,j}}*{{p{x^2}} \over {10000}},} } Zi,j – point height at node i, j of data matrix A.
In the second case (implemented in the presented prototype system), an extra column has been added to the data matrix, containing the differences between the measured height and the constant height of the design plane (Hdiff), calculated at the time of swapping the X, Y, Z data for a given grid cell. Then, to obtain the volume, the column with these differences should be summed up and multiplied by the grid mesh size:
6 where:V = \sum\nolimits_{i = 0}^{rows - 1} {\sum\nolimits_{j = 0}^{cols - 1} {{H_{dif{f_{i,j}}}}} } *{{p{x^2}} \over {10000}}, Hdiffi,j – height difference at node i, j of data matrix A. The script executing the volume calculation for this case is shown in Appendix A as Code 3.
The most advanced case (inclined plane or 3D model) involves adding 2 columns to the data matrix. First (auxiliary) column contains target heights for each grid node, calculated before starting the measurements. Second column contains differences between the measured and target values. Then, as in the previous case (Eq. 5), these differences should be simply summed up and multiplied by the grid mesh size to obtain the volume.
Creating an initial empty matrix for measurement data has its advantages, but to save the current DTM to a file, it is necessary to process it first – by removing grid cells with zero values (where the terrain was not measured). The script that executes this task is included in Appendix A as Code 4.
The described approach to the issue of real-time DTM update is crucial because it reduces operations performed by the computational unit. Coordinate values are not compared iteratively, but are immediately and efficiently assigned to a given mesh. It is an important contribution to the problem of real-time update of DTM in terms of a practical application of the prototype in the future, e.g. as a fully functional component of machine control systems (e.g. for motion optimization).
In order to verify the operation of the algorithm (continuous measuring and updating of the grid DTM model), field measurements have been performed. They included measuring a section of a small gravel mine – a maneuvering area and small gravel piles, pushing the material onto the piles with an excavator and repeating the measurement, but only along the modified piles. The measurement conditions were good – a sunny day, free of dust. Measurement object – mainly gravel, sand and dry soil, slightly moist in the place of modification. The screenshots (Fig. 7) show the results (point cloud straight from the measurement prototype, not modified or filtered in any way, and a mesh model) before and after pushing the material with the excavator. While the material was being pushed in with the excavator, program operation was not interrupted, and the clouds shown here were saved to a file while the program was running.
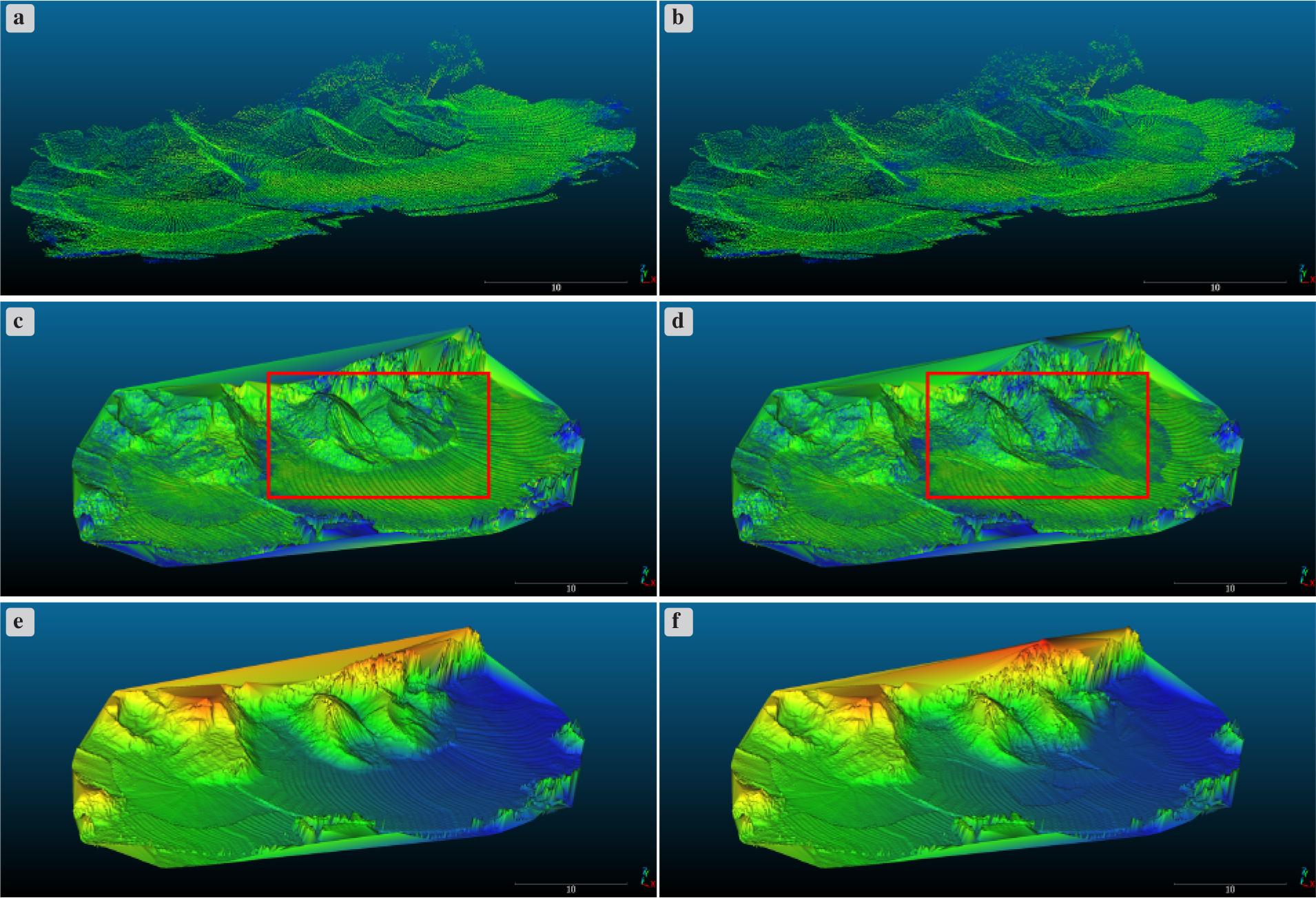
Point cloud (a), b)) and mesh model (c), d), e), f)) from the conducted test measurement: before (a), c), e)) and after (b), d) f)) the pile was modified with an excavator. The colours for graphics a), b), c) and d) are the LiDAR laser beam intensity, while for graphics e) and f) it is the height map. The area of changes has been marked with a red rectangle
In order to lend credibility to the tests and the performance of the presented algorithm, screenshots from the program application are shown in Fig. 8, providing the following information:
the number of LiDAR data packets before pile modification and just before the measurements were completely finished,
the time of taking measurements/screenshots (both from GPS and Windows),
the volume calculated relative to the base plane. Any differences may be due to difficulties in measuring the top of the pile and measurement inaccuracies of the system (the prototype is in the initial stage of development).

Screenshots from the program’s field application. The image a) shows a view of the cloud with LiDAR beam reflectance intensity colors, before the pile was modified. The image b) shows a view of the cloud where the colors of the points are determined by their height, after the pile was modified and the changes captured, just before the program stopped running
This is complemented by a video showing the measurement process, provided in Appendix B. A photos taken before and after the measurements were completed is shown in Fig. 9.

Photos before (a) and after (b) the pile modification. Video from field tests is included in Appendix B
The test was conducted to verify the performance of the proposed real-time DTM update algorithm. The results submitted (Figs. 7–8) suggest that it operates correctly, as points at newly measured locations are continuously replaced with new, up-to-date ones. The successively saved point clouds show the modifications made to the pile and traces on the ground around it. As the measurements were conducted, with the specified measurement parameters (resolution 10 cm, project size 100 x 100 m), no issues with insufficient computing power of the tablet were felt – data packets were received and processed smoothly.
For the purpose of testing the performance of the algorithm, a Microsoft Surface Pro 9 tablet with an Intel i5-1235U processor clocked at 2.50 GHz was used for field work. For the abovementioned measurement parameters, a single iteration of the main loop, corresponding to one rotation of the LiDAR sensor and the update of main data matrix, takes less than 0.001 seconds (Appendix A, Code 2). The computational equipment used is fast enough for the presented prototype to operate and be developed. The time for volume calculation (Appendix A, Code 3) for the mentioned measurement parameters is about 0.002 seconds. The developed algorithm is not without its limitations, however. The first one of them is the size of the NumPy matrix storing the main data matrix. Its size depends mainly on the computer parameters, but also the type of data that the matrix collects. For the presented Microsoft Surface Pro 9 tablet with 16 GB RAM, the maximum size of the data matrix (storing the X, Y, Z coordinates, the intensity of the LiDAR beam reflection and the height difference relative to the base plane for each grid point) must be below 900,000,000 “pixels”. Their number is affected by the preset grid resolution and the size of the project area. Table 1 shows the relationship between grid model resolution and the project size, giving the real picture of the program’s limitations. This limitation can be minimized by using a different computer (one with more RAM), data type (e.g. float32), or programming language (compiled, e.g. C++).
Maximum project dimensions depending on the selected resolution of DTM grid
| Grid resolution (pixel size) [m] | Max project area [m2] | Example dimensions [m] |
|---|---|---|
| 0.01 | 90,000 | 300 × 300 |
| 0.02 | 360,000 | 600 × 600 |
| 0.04 | 1,440,000 | 1200 × 1200 |
| 0.05 | 2,250,000 | 1500 × 1500 |
| 0.10 | 9,000,000 | 3000 × 3000 |
| 0.20 | 36,000,000 | 6000 × 3000 |
| 0.25 | 56,250,000 | 7500 × 3000 |
| 0.50 | 225,000,000 | 15000 × 3000 |
| 1 | 900,000,000 | 30000 × 3000 |
The time needed for volume calculations is another limitation. Calculation time gets higher in proportion to the size of the data matrix, because of the summing up of values in the height difference column (Table 2.). The burden of long calculations for a large data matrix can be reduced by only updating the volume at certain intervals, e.g. every second or every few seconds. It is also possible to change the approach to these calculations by updating the volume at the moment of replacing a given point in the data matrix, without summing up the entire height difference column. This solution will be considered in the future.
Relationship between the grid DTM volume calculation time and the data matrix size
In addition to restricting the maximum size of the project, use of the finest grid resolutions (higher than 5 cm) may also create issues with continuous filling up of all grid nodes. Emerging gaps will result in incomplete data matrix updates due to the lack of currently measured points from the LiDAR sensor at a given location. This is because the sensor can collect a limited amount of data in a given unit of time (~300,000 pts/s for the full 360° horizontal angle and vertical angle of ±15°, in single return mode [44]). The problem can be solved e.g. by using linear interpolation which, however, is not yet being implemented (mainly because a higher resolution is not needed for earthworks). Therefore, in order to make sure the grid cells are filled in correctly, the speed of machine movement must be adjusted (limited) appropriately. Accordingly, analysis has been carried out to show how the LiDAR rotation speed and the movement speed affect the resolution of measurements that can ultimately be obtained:
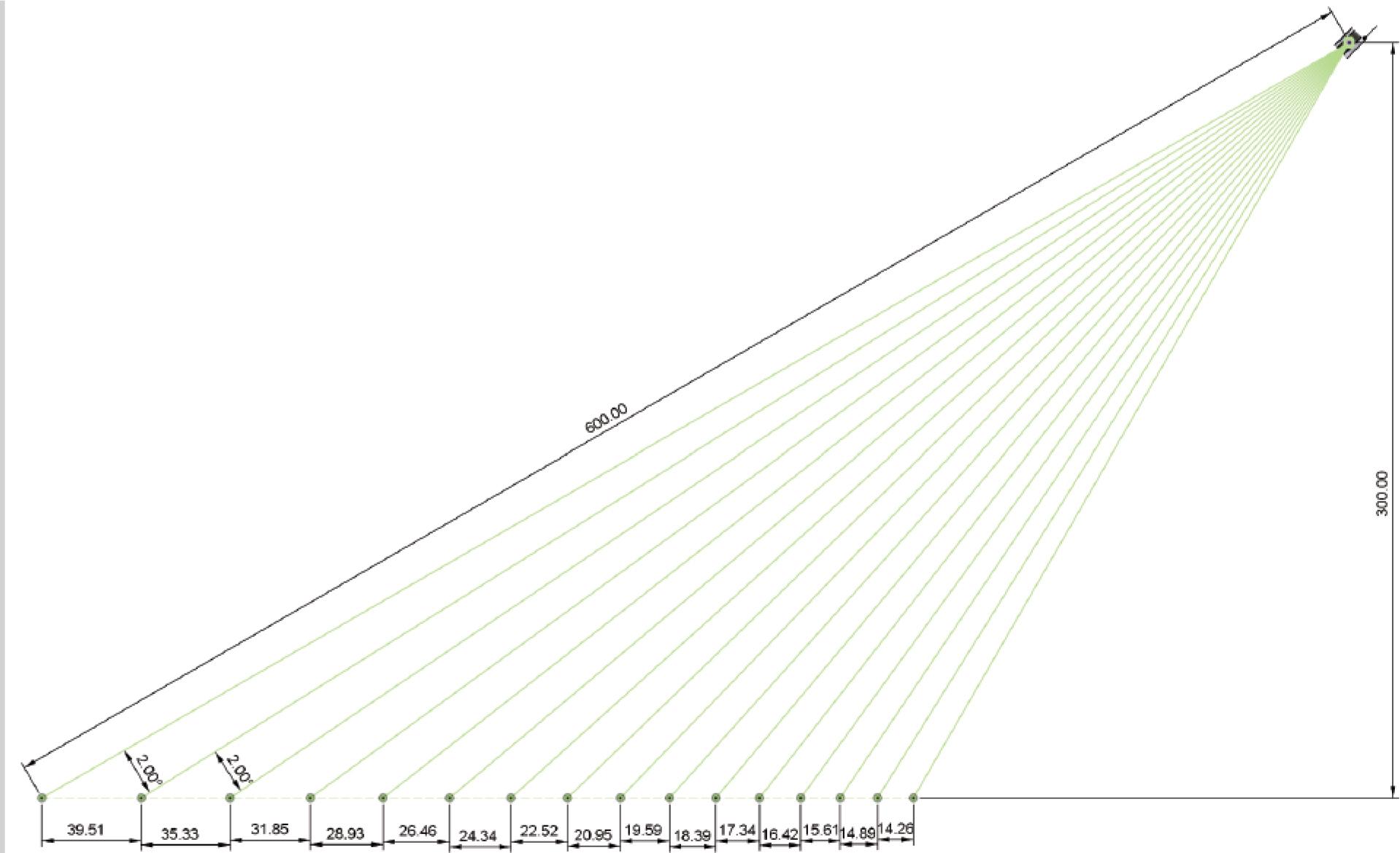
Table 3 shows the relationship of the distance between successive points of the same channel/beam (azimuthal resolution) in the horizontal plane at the tested distance of 6 m and the LiDAR rotational speed – revolutions per minute (RPM). As can be seen, the resolution is very high, considering it is to be applied in construction works. It is therefore possible to select even the highest rotational speed, as ultimately that would not have a very negative impact on the azimuthal resolution, while it might have a positive impact on the radial resolution. Consequently, it has been decided to increase the standard rotation speed of the LiDAR from 600 RPM to 900 RPM. A decision was taken not to use the maximum rotational speed of 1200 RPM, so as to avoid overloading sensor bearings, and thus raising the temperature of the sensor.
Figure 10 shows distances on the ground between points from all the 16 LiDAR channels, with the sensor mounted as specified. As can be seen, these distances are significant. As the platform moves, the points from successive measurements will begin to overlap. Therefore, the moving speed determines how the measurement area will be covered with successive points.
Table 4 shows the dependence of the moving speed (assuming the rotational speed of the LiDAR sensor is 900 RPM) on terrain coverage with measurements. The first thing that can be noticed is the irregularity of the maximum observed gap that can occur in the grid that is being logged. It is mostly determined by the random factor, because in field conditions it is very difficult to achieve a perfectly constant moving speed and a smooth terrain surface. It can therefore be assumed that the fitted trend line correctly answers the question of what moving speed corresponds to the maximum possible grid resolution. At low speeds, many points practically overlap with each other, hence the fitted line is not significantly inclined and the resolution does not decrease proportionally to the increase in moving speed.
Distances [cm] on the ground between points from all the 16 LiDAR channels, with the sensor mounted as specified: 3 m above the ground, at an angle of 45°, maximum distance 6 m
Dependence of the azimuthal resolution at a distance of 6 m on the rotational LiDAR speed
Dependence of the moving speed (assuming the rotational speed of the LiDAR sensor is 900 RPM) on terrain coverage with measurements
When it comes to the design of the platform itself and the sensors within it, certain limitations may arise. Primarily, GNSS signal reception can be problematic when operating in dense urban areas, among trees, or under structures. Mounting the platform on the machine's roof and operating outdoors can virtually eliminate this problem. In the case of a LiDAR sensor, reflections from mirrored and semi-transparent surfaces can be problematic. However, construction sites primarily consist of soil and various types of bulk materials, which should not pose a challenge for this type of sensor. The only real obstacle may be dust floating behind the machine during operation. This problem can be partially eliminated by using appropriate filtration, for example, based on the intensity of the laser beam’s reflection and proximity to other nearby measured points, as described in [45]. At the time of publication, the measurement platform is not designed for operation in harsh field conditions, except for data recording interruption in the absence of a FIXED position solution for both GNSS receivers. More advanced solutions are planned for future implementation.
The work carried out and the analysis of the collected test data allowed for the evaluation of the performance of the proposed measurement platform and processing algorithm. For the purposes specified at the beginning (measurements on construction sites and machinery control systems), the use of resolutions ranging from 10 to 25 cm seems most reasonable for several reasons:
Work can be performed on a larger project area.
No issues with filling in the DTM grid meshes, even at high speeds of the measuring platform.
In any case, the specified resolution is several times higher than one a surveyor would ever use to measure the terrain using a total station or GNSS receiver and, as verified by the studies [46], increasing the resolution does not significantly affect the result of volume calculations.
Ongoing volume calculations would not pose any problems due to the large size of data matrix.
Working with a bulldozer, grader or excavator involves producing flat areas with large surfaces, so resolution based on single centimetres is normally not needed.
For the purpose of acquiring data from the level of earthworks machines, modern low-cost LiDAR scanners provide sufficient speed and resolution. Despite the small number of channels/scanning beams, these sensors can be used successfully, because the appropriate resolution can be obtained thanks to the movement of the machine and the overlap of subsequent beams on the mapped area. However, the measurement system settings should take into account the machine's speed, especially when high resolution of the acquired point cloud is required. In addition, the sensor’s rotational speed should be taken into account to avoid hardware overload.
The algorithm was shown to be correct and effective using a mid-range processor to process real-time measurement data. The presented system and algorithm are efficient enough for typical DTM update needs for earthworks, despite the fact that a low-level programming language was not used.