Finite-Element Analysis of Flexural Behaviour of Timber-Glass Composite I-Beams Cover

.blurhash-client-img { display: none !important; }

Finite-Element Analysis of Flexural Behaviour of Timber-Glass Composite I-Beams

Architecture, Civil Engineering, Environment

Volume 18 (2025): Issue 3 (September 2025)

By: Marcin KOZŁOWSKI, Erik SERRANO, Magdalena MROZEK and Dawid MROZEK

Open Access

|Sep 2025

Figures & Tables

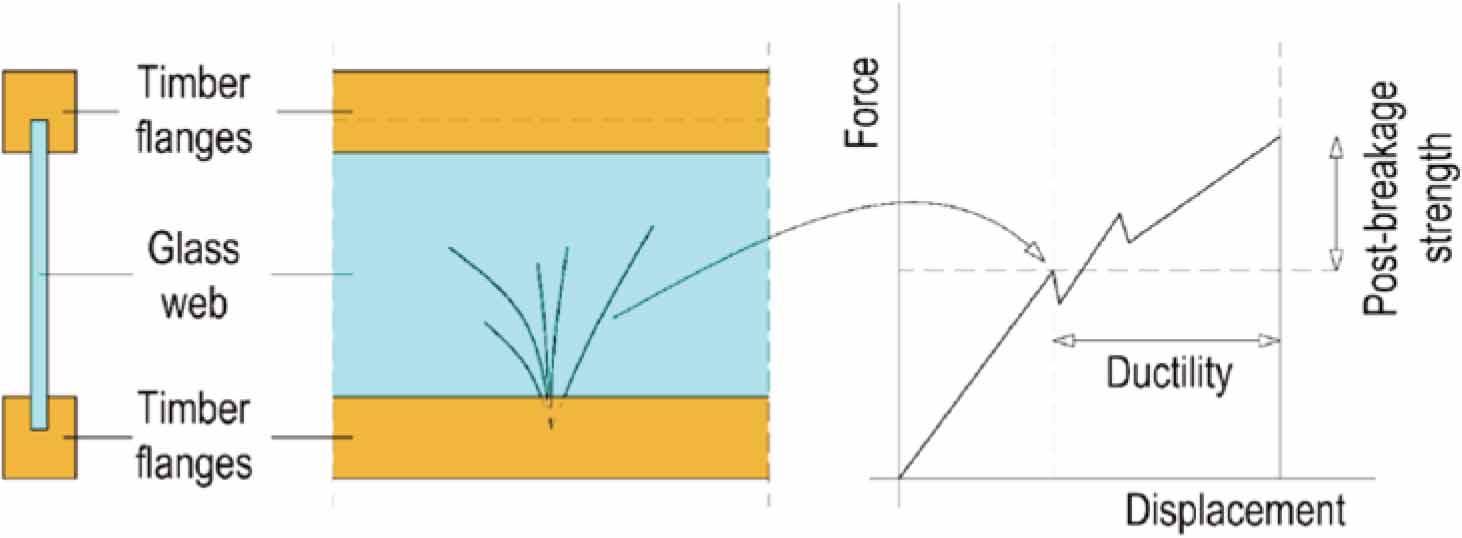
Schematic representation of timber-glass composite beam concept: cross-section of hybrid beam (left), side-view of hybrid beam with cracked glass web (middle), force-displacement diagram showing ductility and post-breakage strength (right)

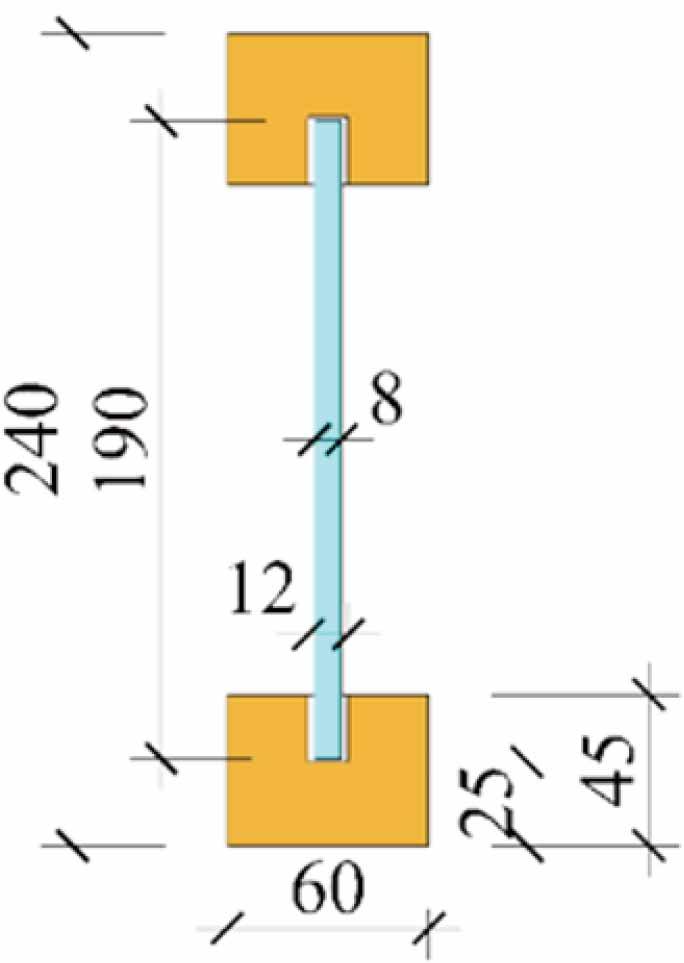
Cross-section of timber-glass composite beams: type TGCB1

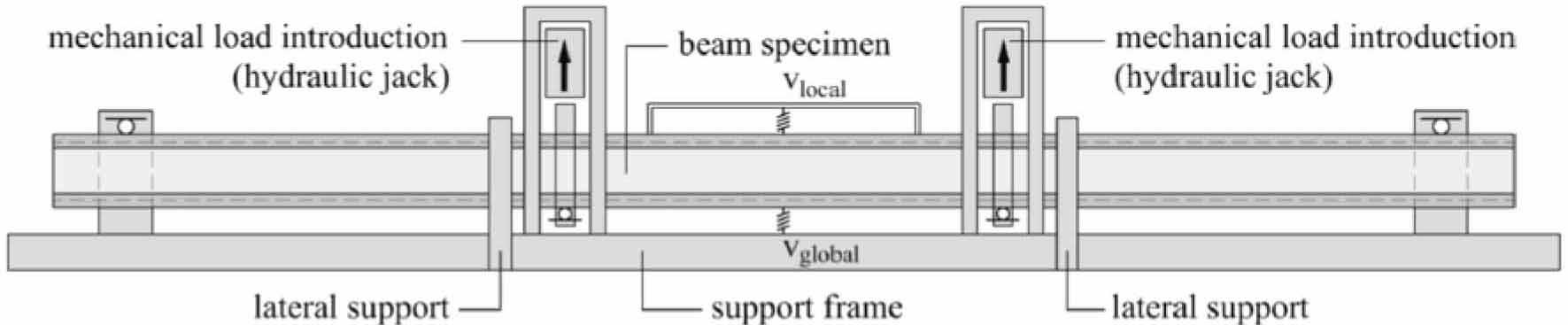
Four-point bending set-up

Experimental load-displacement plots for beams type TGCB1 obtained from the four-point bending tests [26,27,28]. Notation: E = Epoxy, A = Acrylate, S = Silicone, AF = annealed float, HS = heat-strengthened

Experimental load-displacement plots for beams type TGCB2 obtained from the four-point bending tests [13,14]. Notation: A = Acrylate, S = Silicone, LN = large groove (no edge treatment), SP = small groove (polished edges)

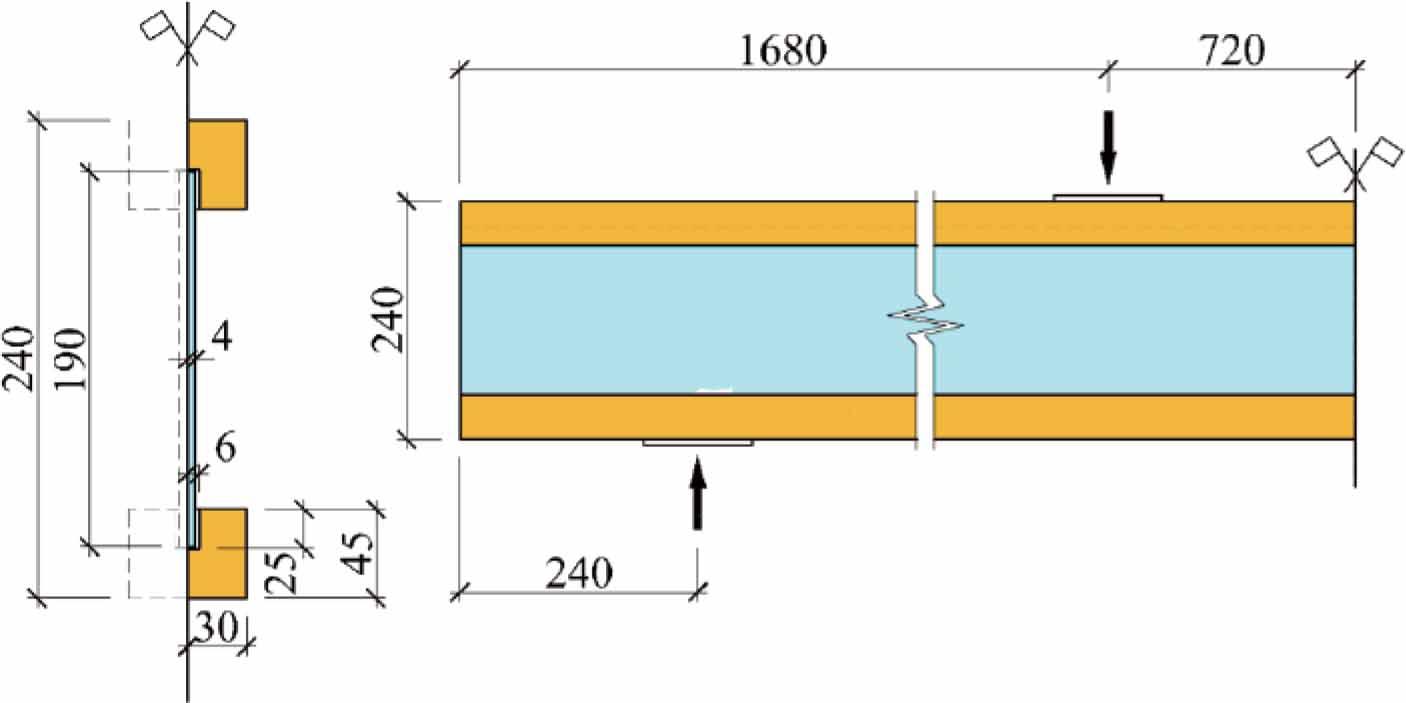
Cross-section, loading and boundary conditions for numerical model of beam type TGCB1

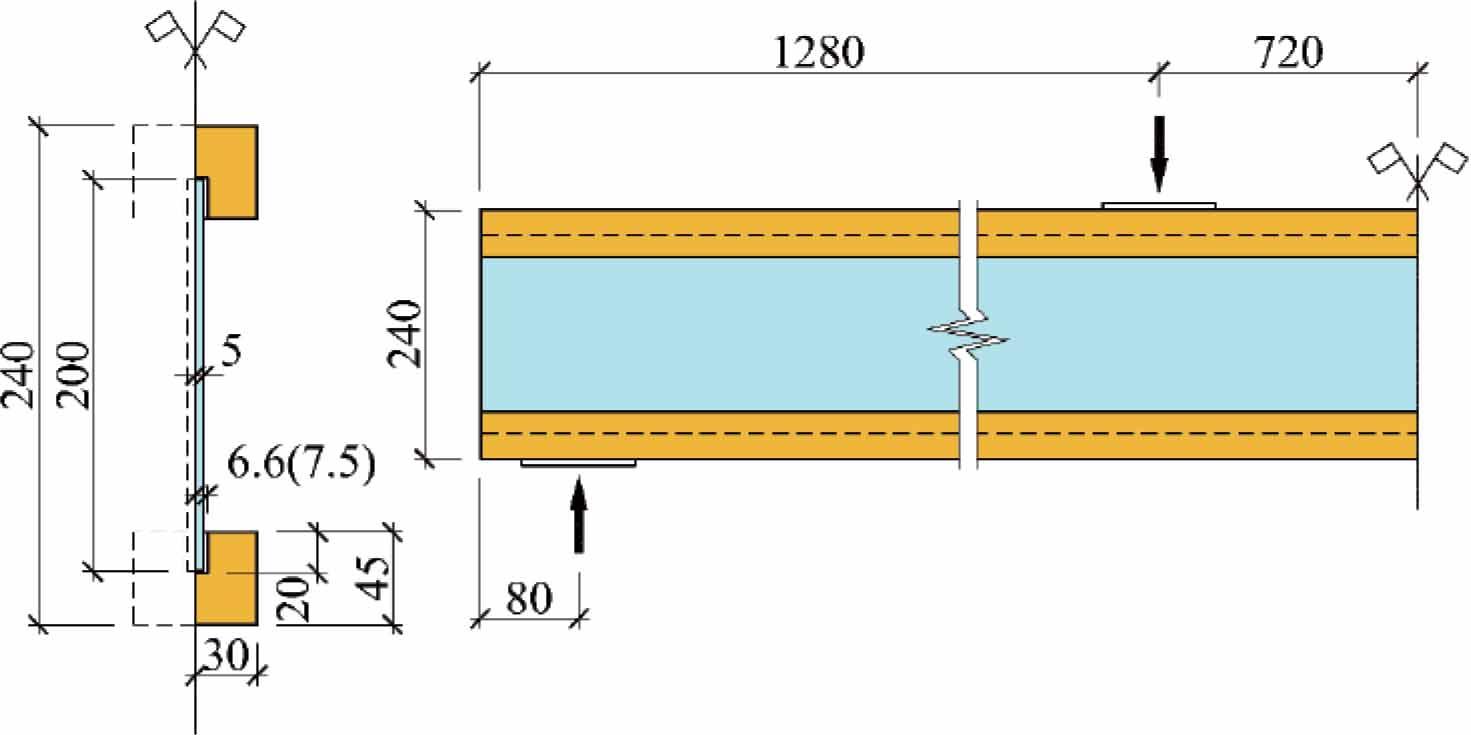
Cross-section, loading and boundary conditions for numerical model of beam type TGCB2

Crack criterion in Mode I and post-failure stress-fracture energy curve

Traction-separation Law as damage definition

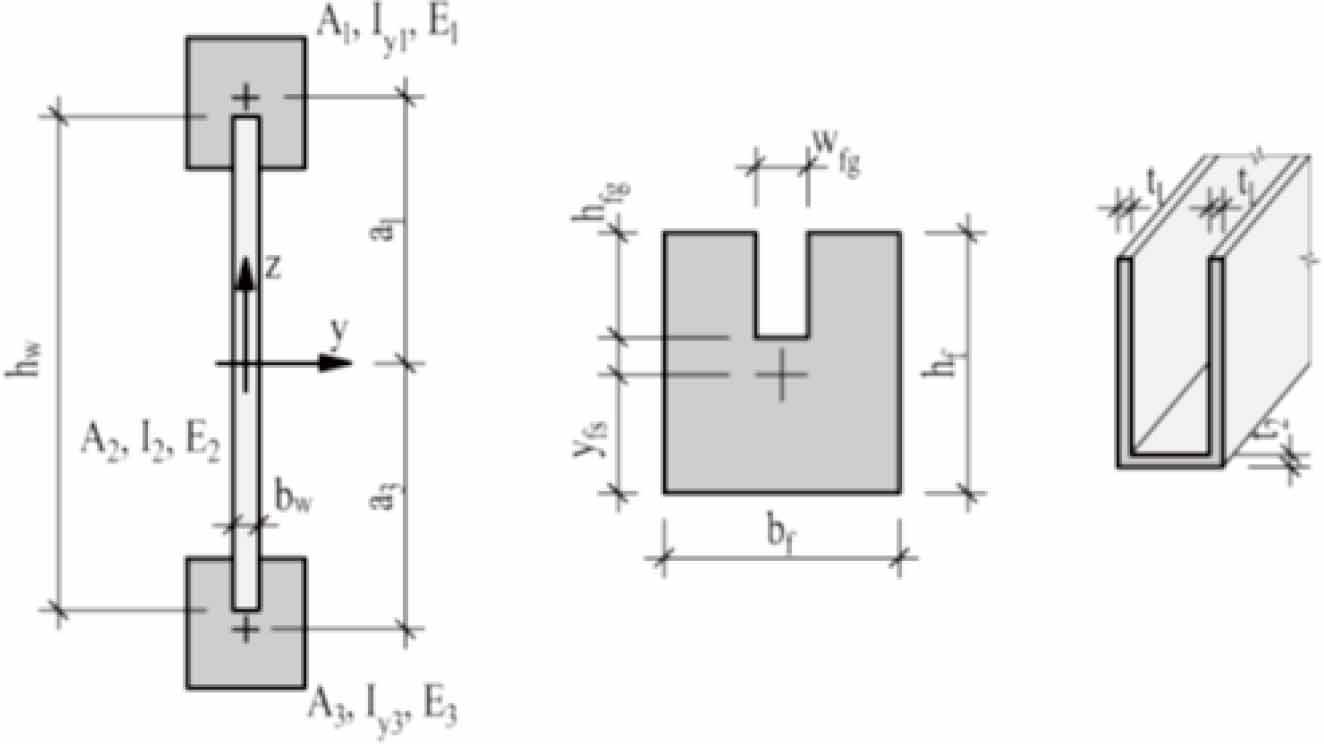
Notation system for the cross-section (left), timber flange (center) and bond connection (right).

Plot of the change in load-displacement of the TGCB1 beam (silicone adhesive) as a function of the glass web material model used, together with locations of probable damage from Implicit analysis

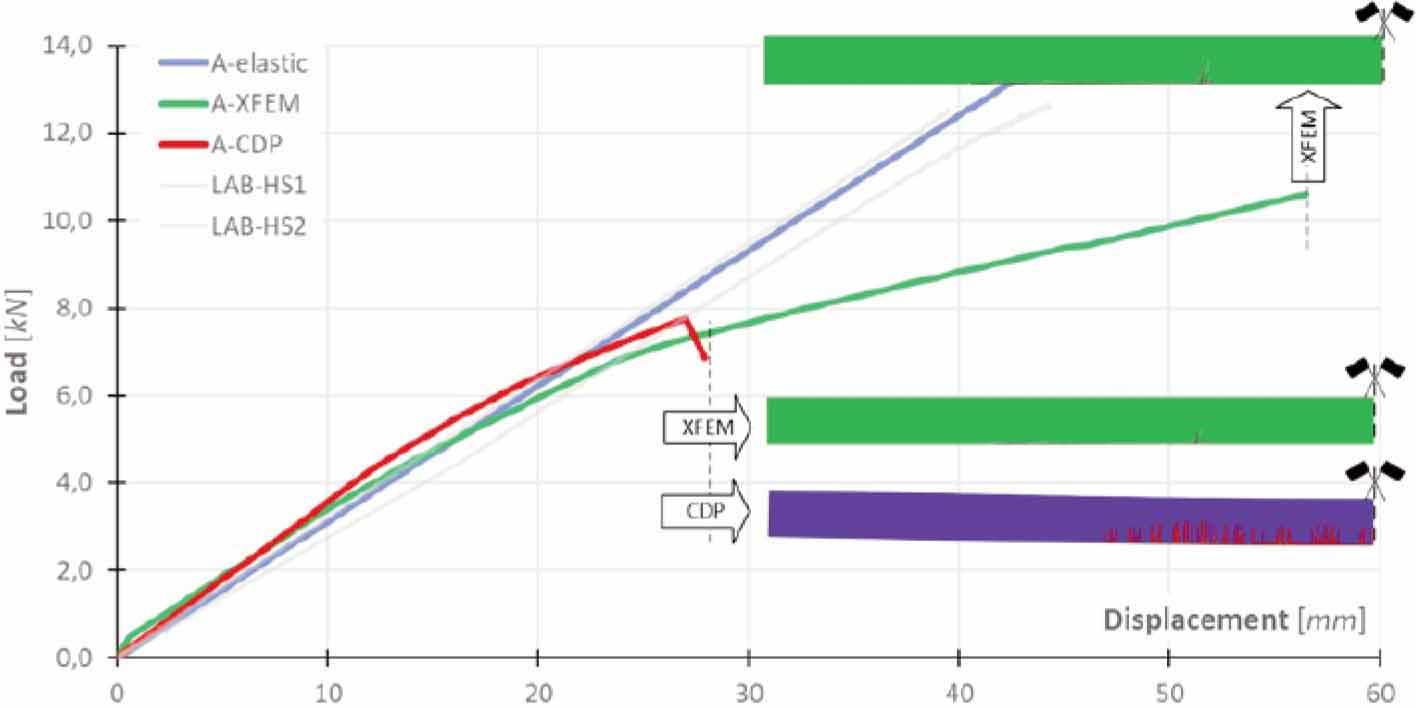
Plot of the change in load-displacement of the TGCB1 beam (acrylate adhesive) as a function of the glass web material model used, together with locations of probable damage from Implicit analysis

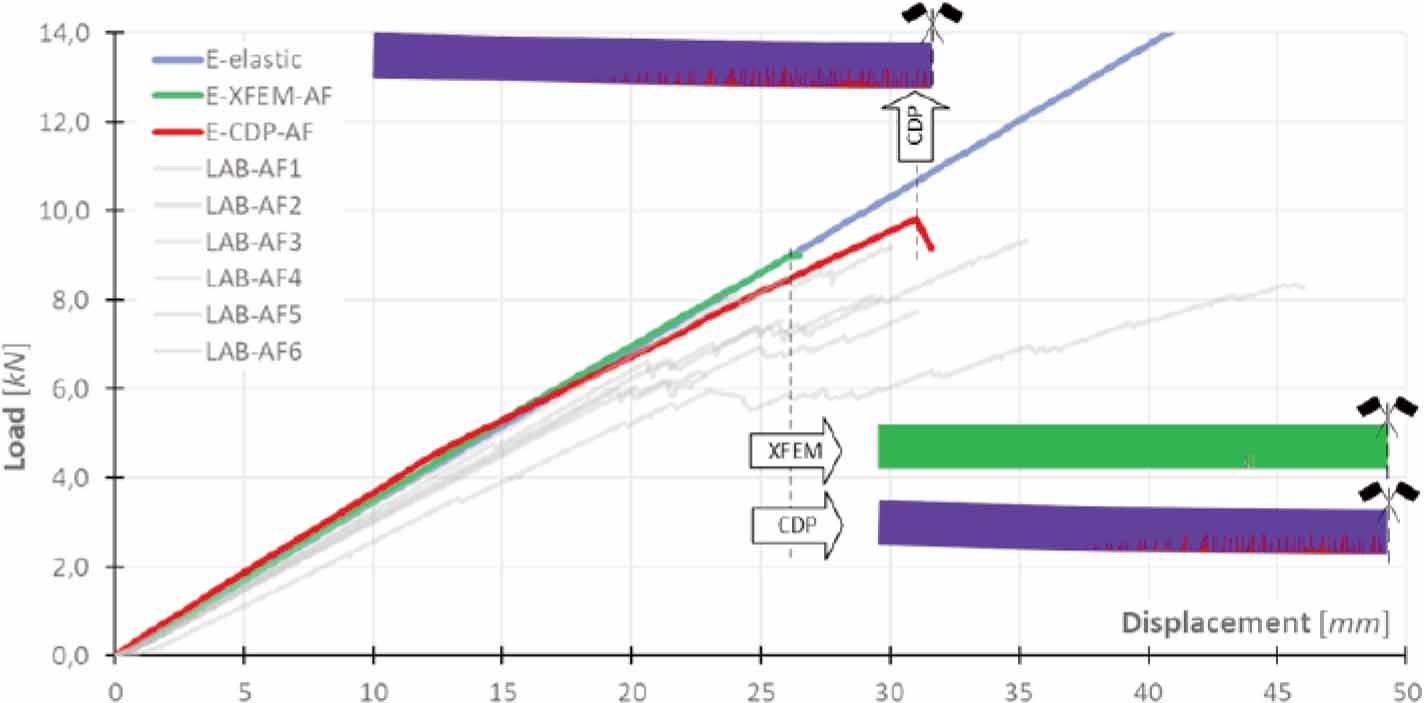
Plot of the change in load-displacement of the TGCB1 beam (epoxy adhesive) as a function of the glass web material model used, together with locations of probable damage from Implicit analysis

Plot of change in stiffness of TGCB1 beam to percentage of displacement using Silicone as adhesive

Plot of change in stiffness of TGCB1 beam to percentage of displacement when using Acrylate as adhesive

Plot of change in stiffness of TGCB1 beam to percentage of displacement when using Epoxy as adhesive

Progressive failure of reference model. Load-displacement plot (a), comparison of crack patterns in glass web at different failure stages and displacements (b-d). Note symmetry of model at right vertical edge

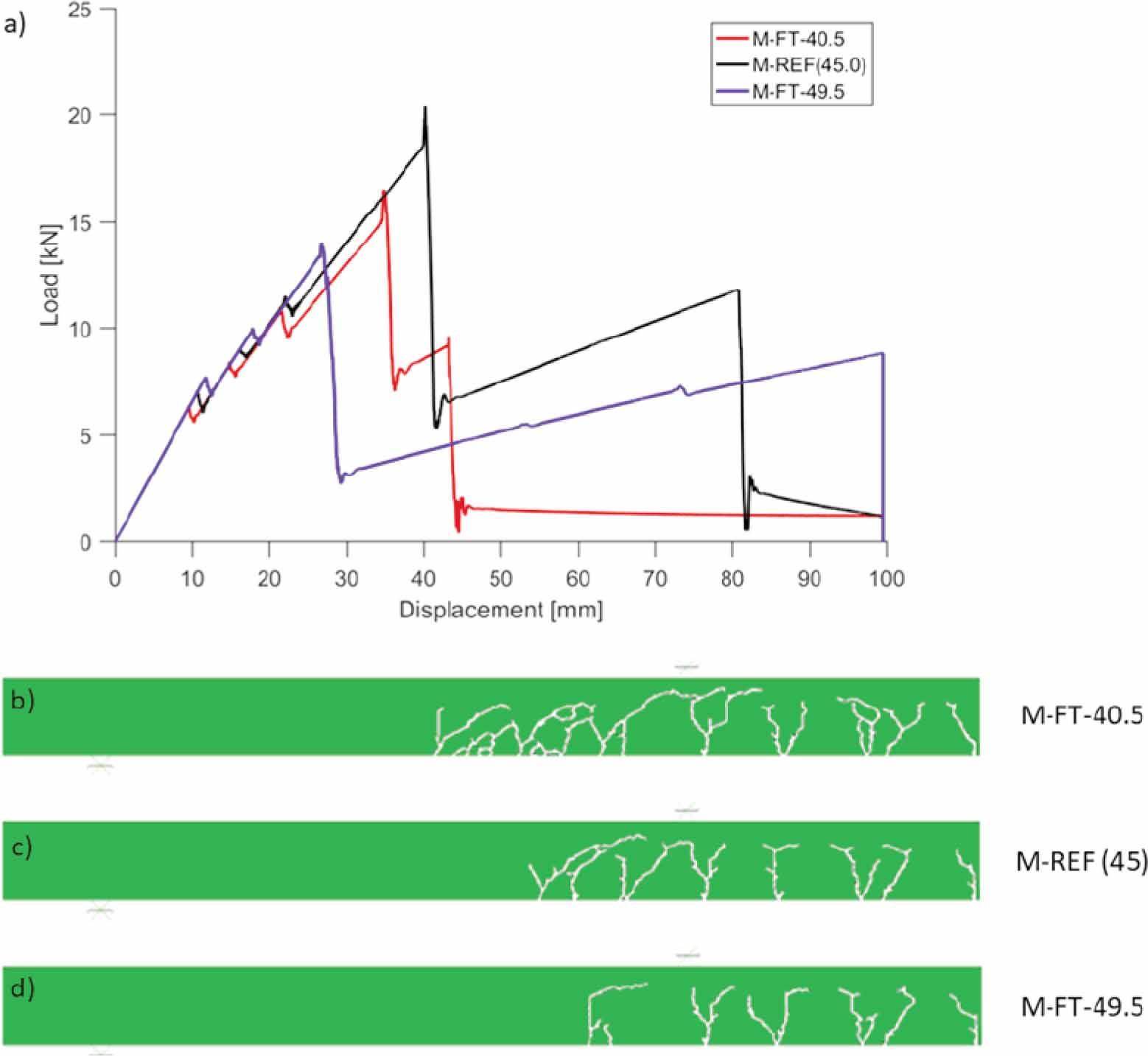
Effects of tensile strength of glass. Comparison of load-displacement plots (a), comparison of crack patterns in glass web at displacement of ≈ 23.8 mm (b-d). Note symmetry of numerical model at right vertical edge

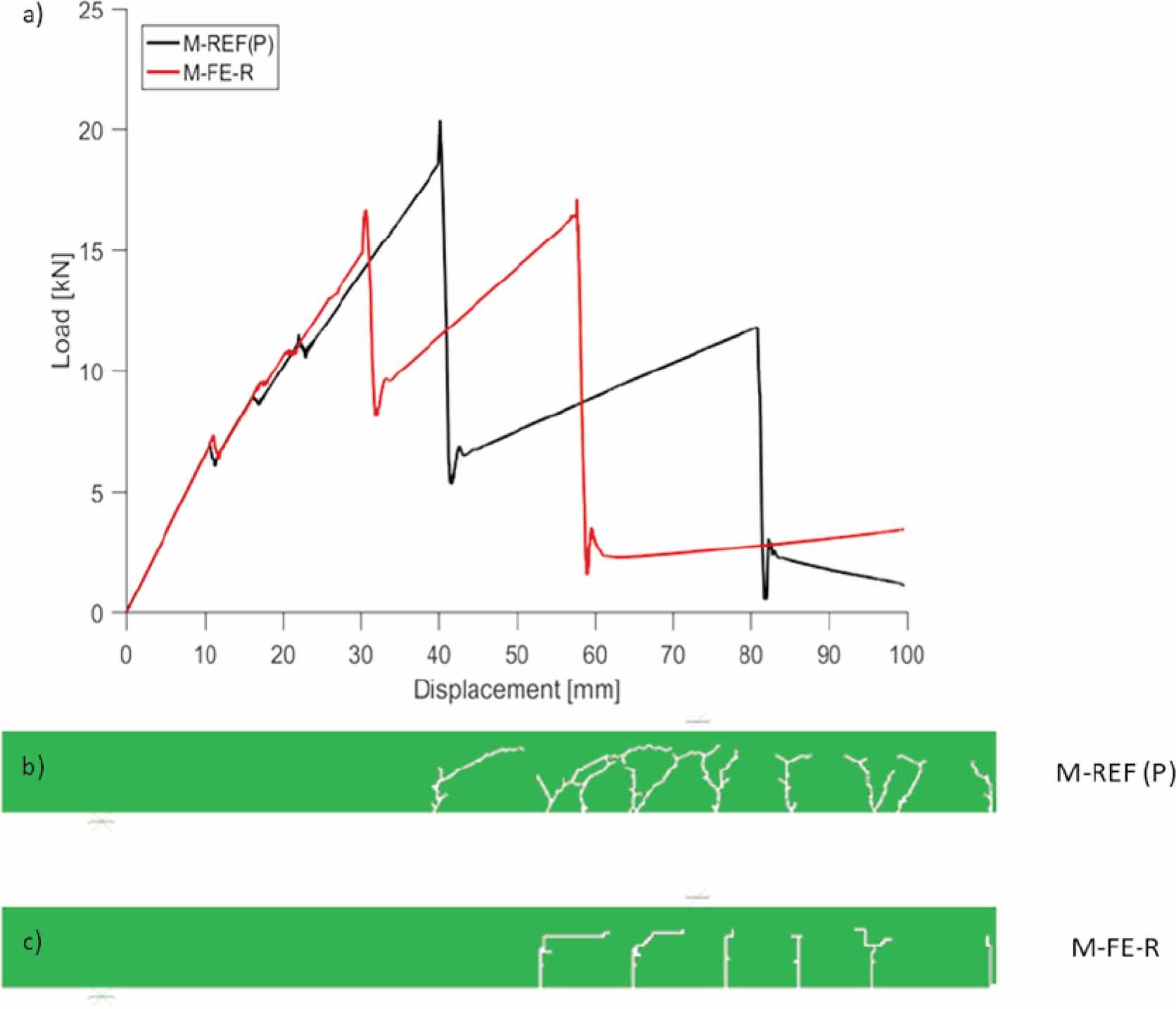
Effects of FE geometry. Comparison of load-displacement plots (a), comparison of crack patterns in glass web at displacement of ≈ 23.8 mm (b, c). Note symmetry of numerical model at right vertical edge

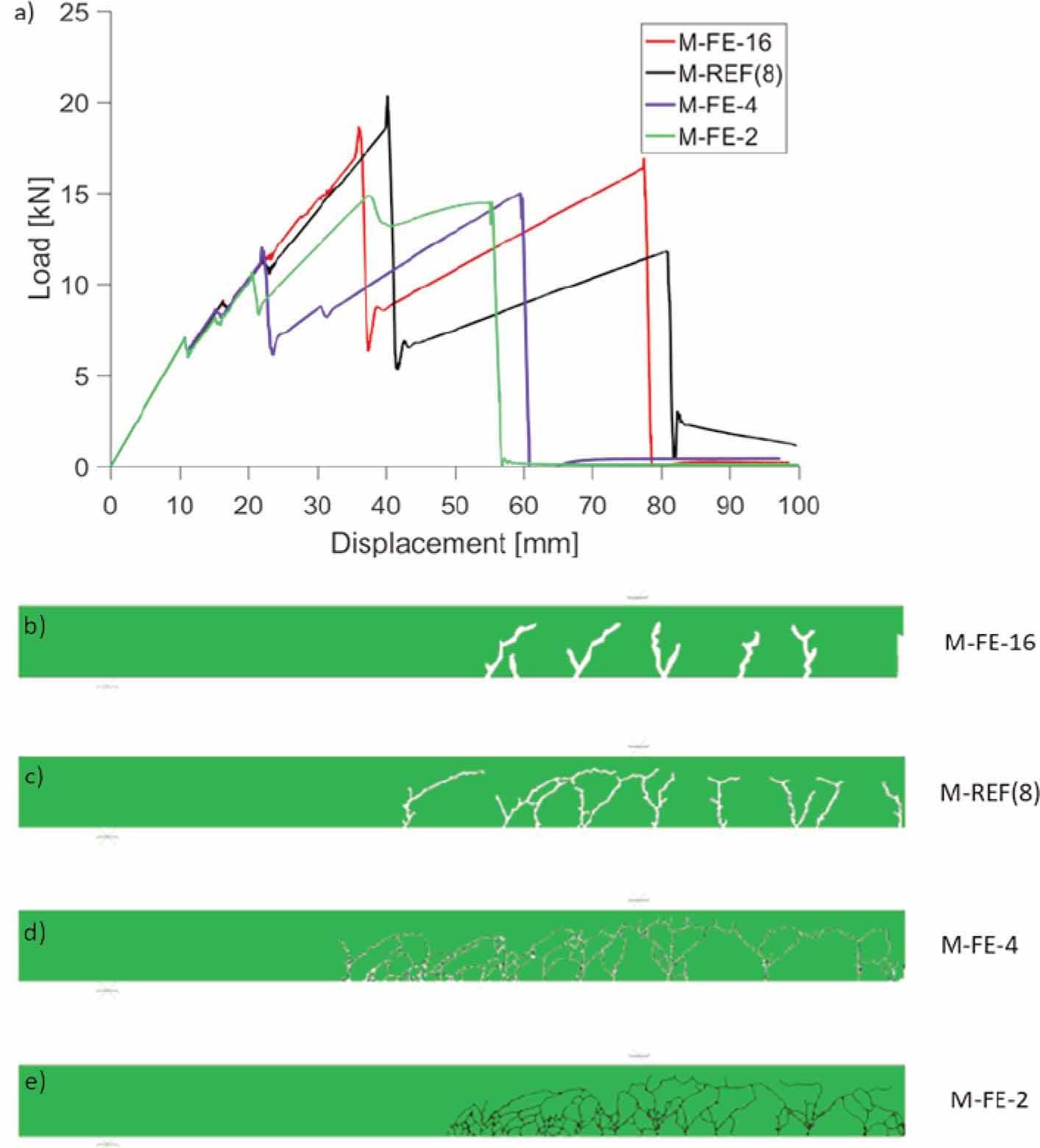
Effects of FE size. Comparison of load-displacement plots (a), comparison of crack patterns in glass web at displacement of ≈ 23.8 mm (b-e). Note symmetry of numerical model at right vertical edge

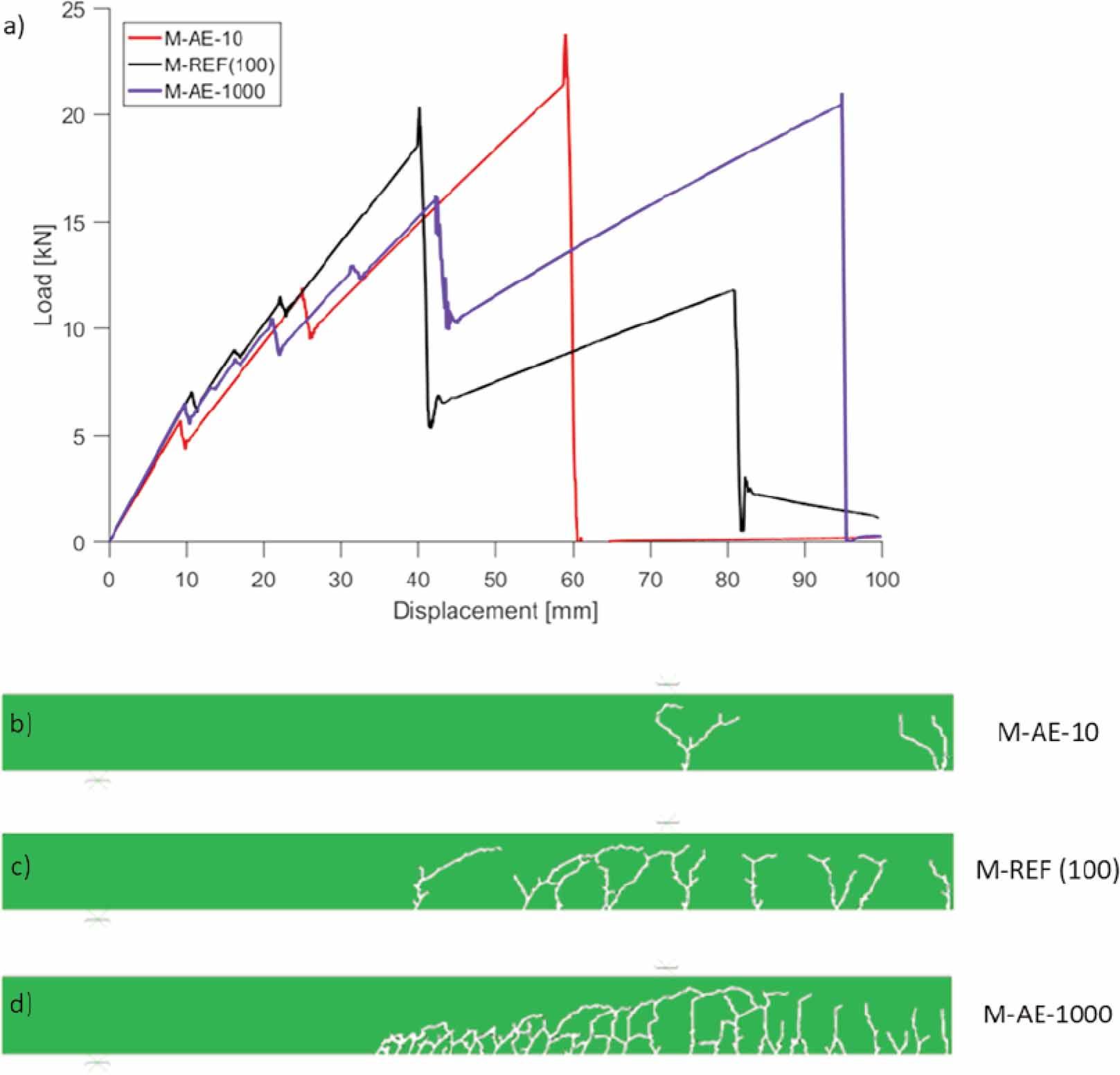
Effects of adhesive stiffness. Comparison of load-displacement plots (a), comparison of crack patterns in glass web at displacement of ≈ 23.8 mm (b-d). Note symmetry of numerical model at right vertical edge

Comparison between numerical and experimental [27] loaddisplacement plots for the beam TBCB1_E_AF. Effects of different tensile strength of glass

Comparison between numerical and experimental [13,14] load-displacement plots for the beam type TBCB2

Experimental results (mean values and standard deviations) for beam specimens [13,14,26,27,28] and corresponding FE and analytical predictions_ Notation: PBSI – Post-breakage strength index PBSI = 100 × (Finit - Fult) / Fult_, PCDI - Post-cracking ductility index, PCDI = 100 × (uinit - uult) / uult, FE = 100 × (resultFE – resultEXP) / resultEXP, AN = 100 × (resultAN – resultEXP) / resultEXP

	Experiments					Finite Element						Analytical
Beam model	F_int [kN]	F_ult [kN]	PBSI [%]	PCDI [%]	K_init [MNm²]	Model	F_int [kN]	F_ult [kN]	PBSI [%]	PCDI [%]	K_init [MNm²]	F_int [kN]	K_init [MNm²]
TGCB1_E_AF	11.6 (2.8)	16.4 (2.2)	51.5 (50)	91.2 (86.7)	0.898 (0.042)	E_AF_FE_FT45	7.2	12.2	70.6	176.9	0.920	7.5	0.817
						Δ_FE/Δ_AN=	-38.4%	-25.7%	41.3%	94.3%	0.920	4.9%	0.817
						E_AF_FE_FT66	10.5	15.6	48.2	109.7	2.5%	10.9	-9.0%
						Δ_FE/Δ_AN=	-9.3%	-4.94%	-3.6%	20.5%		3.6%
TGCB1_E_HS	25.5 (-)	25.5 (-)	-	-	0.898 (-)	E_HS_FE_FT45	25.5	25.5	-	-		24.5
TGCB1_E_HS	25.5 (-)	25.5 (-)	-	-	0.898 (-)	Δ_FE/Δ_AN=	0.1%	0.1%	-	-		-3.9%
TGCB1_A_HS	25.5 (-)	25.5 (-)	-	-	0.907	A_HS_FE_FT45	24.6	24.6	-	-	0.904	24.4	0.808
TGCB1_A_HS	25.5 (-)	25.5 (-)	-	-	0.907	Δ_FE/Δ_AN=	-2.4%	-2.4%	-	-	-0.3%	-3.9%	-10.6%
TGCB1_S_HS	19.8 (-)	19.8 (-)	-	-	0.720	S_HS_FE_FT45	18.3	18.3	-	-	0.692	19.1	0.630
TGCB1_S_HS	19.8 (-)	19.8 (-)	-	-	0.720	Δ_FE/Δ_AN=	-7.7%	-7.7%	-	-	-3.9%	-3.5%	-12.5%
TGCB2_A_AF_L	11.1 (1.3)	28.3 (2.4)	158 (24.0)	298 (51.2)	1.253 ()	A_AF_FE_L_ FT45	10.3	27.0	162	325.5	1.349	9.4	1.069
TGCB2_A_AF_L	11.1 (1.3)	28.3 (2.4)	158 (24.0)	298 (51.2)	1.253 ()	Δ_FE/Δ_AN=	-7.4%	-4.7%	4.9%	8.9%	7.66%	-15.3%	3.8%
TGCB2_A_AF_S	13.0 (1.1)	28.7 (2.3)	122 (24.0)	210 (39.0)	1.237 ()	A_AF_FE_SG_FT45	10.5	21.8	108	302	1.367	9.6	1.081
TGCB2_A_AF_S	13.0 (1.1)	28.7 (2.3)	122 (24.0)	210 (39.0)	1.237 ()	Δ_FE/Δ_AN=	-19.2%	-23.8%	-11.4	-43.6%	10.5%	-26.2%	6.3%
TGCB2_S_AF_L	8.8 (-)	20.3 (-)	131 (-)	536 (-)	0.918 (-)	S_AF_FE_SG_ FT45	8.2	22.8	179	465	1.075	7.4	0.826
TGCB2_S_AF_L	8.8 (-)	20.3 (-)	131 (-)	536 (-)	0.918 (-)	Δ_FE/Δ_AN=	-6.9%	12.4%	36.7%	-13.3%	17.1%	-15.9%	-10.0%

Material properties used in numerical models for timber [27, 42]

Material	E_t,l	E_t,r	E_t,t	ν_{t, lr}	ν_lt	ν_rt	G_lr	G_lt	G_rt	ρ_t	f_t
	[MPa]	[MPa]	[MPa]	-	-	-	[MPa]	[MPa]	[MPa]	[kg/m³]	[MPa]
Pine wood	12 410	880	880	0.44	0.40	0.52	1 090	1 090	140	510	34.9
LVL	11 600	750	750	0.44	0.40	0.52	930	930	120	510	50

Material properties used in numerical models for adhesives [27]

Adhesive	ρ [kN/m³]	E [MPa]	ν [-]
Silicone	5	3	0.49
Acrylate	5	100	0.40
Epoxy	5	1 595	0.46

Overview of TGCB1, manufactured beam type TGCB1, n is the number of specimens produced

Beam type	Adhesive	Glass type	Length [mm]	Total height [mm]	Glass pane size [mm²]	Glass thickness [mm]	Timber block size [mm²]	Groove size [mm]
TGCB1	Epoxy (n=6)	Annealed float	4800	240	4800×190	8	45×60	12×20
	Epoxy (n=2) Acrylate (n=2) Silicone (n=2)	Heat-strengthened	4800	240	4800×190	8	45×60	12×20

Overview of manufactured beams, type TGCB2, n is the number of specimens produced [13,14]

Beam type	Adhesive	Glass type	Length [mm]	Total height [mm]	Glass pane size [mm²]	Glass thickness [mm]	Timber block size [mm²]	Groove size [mm]
TGCB1	(n=1)	Annealed float	3500	240	3500×200	10	45×60	13(15)×25

Mechanical and geometrical properties of parametric models_ Notation: R = Rectangular, P = Prism

Variation	FE/model	f_t [MPa]	FE size [mm]	FE geometry [-]	E_int [MPa]
Reference	M-REF	45.0	8	P	100
Variation of tensile strength of glass	M-FT-40.5	40.5	8	P	100
Variation of tensile strength of glass	M-FT-49.5	49.5	8	P	100
Variation of FE size	M-FE-R	45	8	R	100
Variation of FE geometry	M-FE-16	45	16	P	100
	M-FE-4	45	4	P	100
	M-FE-2	45	2	P	100
Variation of adhesive stiffness	M-AE-10	45	8	P	10
Variation of adhesive stiffness	M-AE-1000	45	8	P	1000

DOI: https://doi.org/10.2478/acee-2025-0039 | Journal eISSN: 2720-6947 | Journal ISSN: 1899-0142

Journal RSS Feed

Language: English

Page range: 165 - 189

Submitted on: Apr 11, 2024

|

Accepted on: May 28, 2025

|

Published on: Sep 30, 2025

Published by: Silesian University of Technology

In partnership with: Paradigm Publishing Services

Publication frequency: 4 issues per year

Keywords:

Structural glass,

Timber-glass beams,

Glass cracking,

Numerical modelling,

Related subjects:

Architecture and design,

Architects, buildings

© 2025 Marcin KOZŁOWSKI, Erik SERRANO, Magdalena MROZEK, Dawid MROZEK, published by Silesian University of Technology
This work is licensed under the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 License.

Previous article Volume 18 (2025): Issue 3 (September 2025)Next article