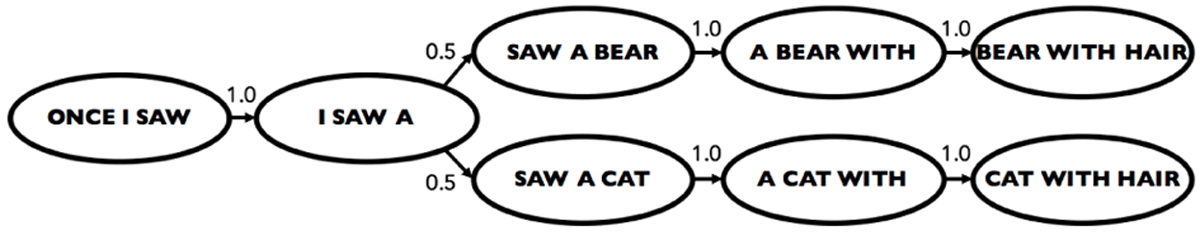
Figure 1
Transition probabilities for a 3rd-order Markov model over words. The model has been trained on the phrases “once I saw a bear with hair” and “once I saw a cat with hair”. Each state in this model is a tuple of 3 elements and transitions are between tuples that overlap by all but one element. Note that though a path through this model will have length 5, the generated token sequence will have length 7 (i.e., element sequence length + order – 1).
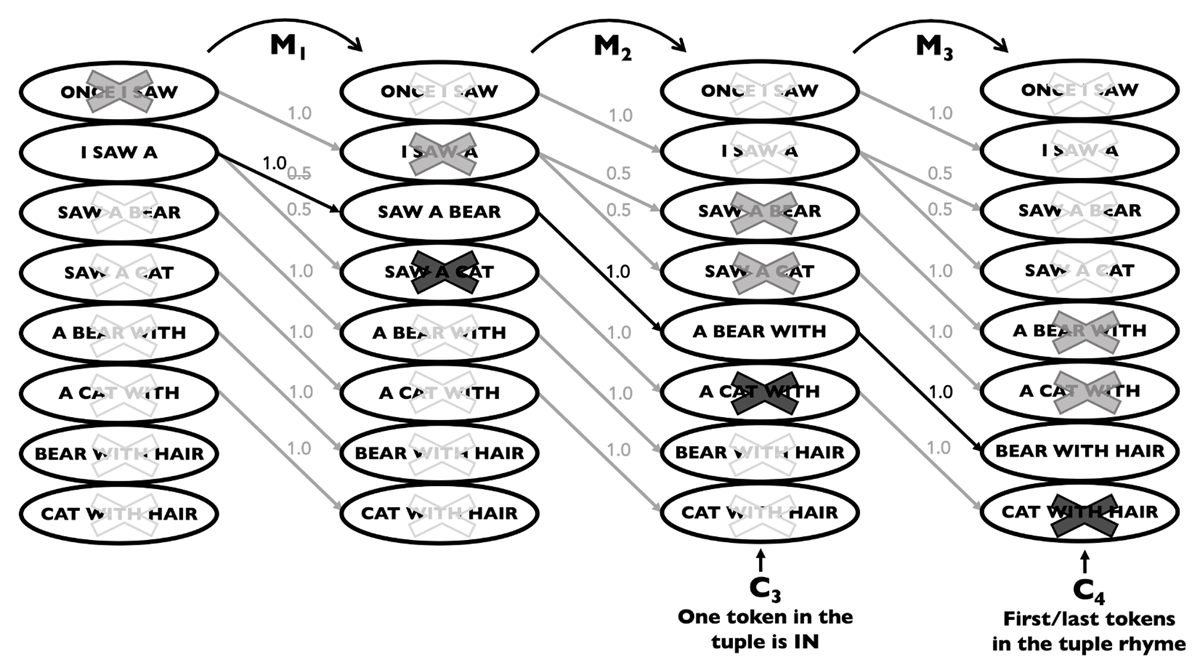
Figure 2
Transition probabilities for a 3rd-order NHMM of length 4. This model is built from the Markov model in Figure 1. The diagram shows the result of first modifying transition matrices M1,M2, and M3 according to two unary constraints: C3 = (X3, {x | x is a tuple of words containing at least one preposition}) and C4 = (X4, {x | x is a tuple of words in which the first and last words rhyme}). States marked with a white ‘X’ are pruned due to the length constraint (i.e., transitions through these states do not result in element sequences of length 4). States marked with a gray ‘X’ are pruned due to the addition of the C3 constraint. This constraint is an example of a floating constraint in that the part of speech (POS) constraint is effectively satisfied by any satisfying token appearing at sequence positions 3, 4, or 5. States marked with a black ‘X’ are pruned due to the further addition of the C4 rhyme constraint. The C4 constraint is an example of a dynamic constraint in that in the 6-word sequence generated from the model, the rhyme group relating the 4th and 6th words is dynamically chosen at run time. Grey transitions represent transition probabilities that are zeroed as a result of applying or ensuring arc-consistency of constraints.
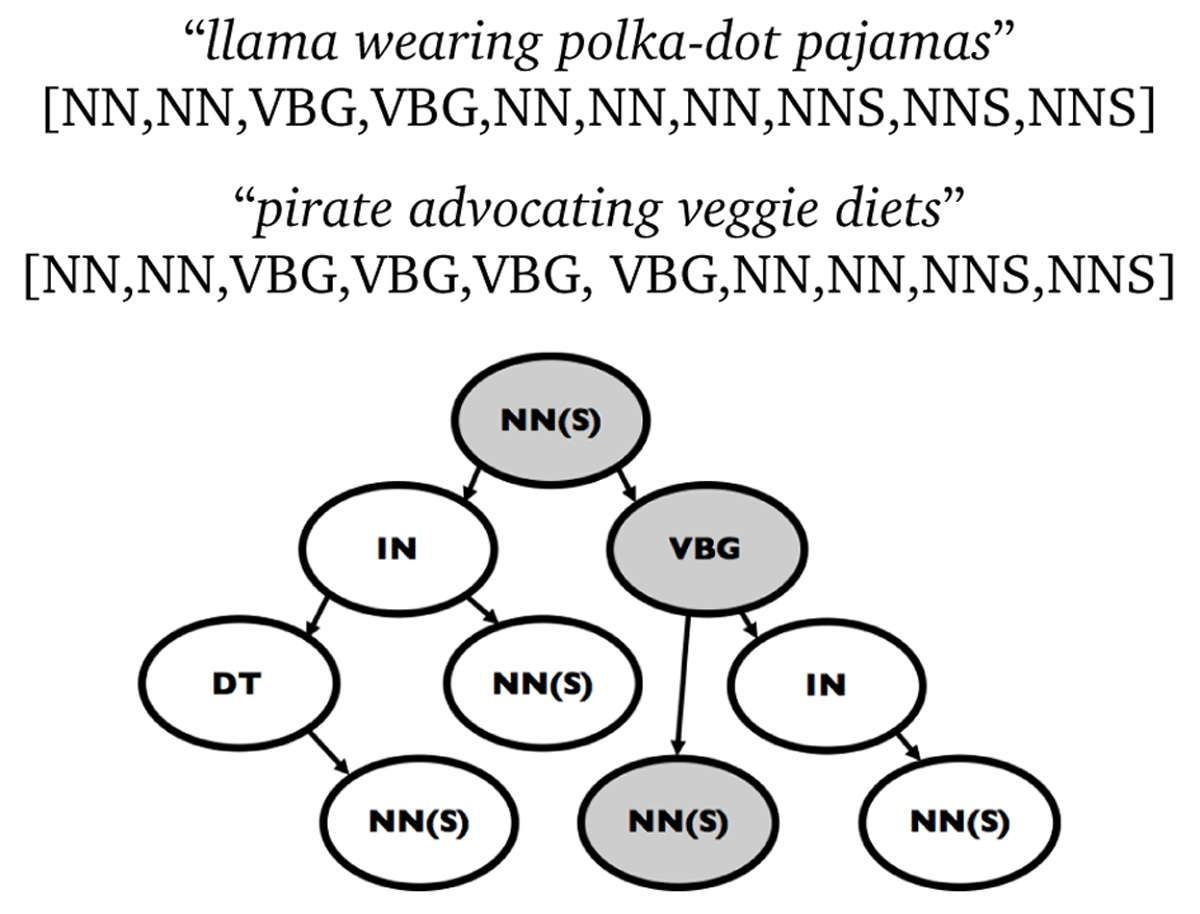
Figure 3
Floating syntax constraints. Shown are two 10-syllable phrases representing a transition between two 9-length syllable tuples in a 9th-order NHMM, each with its syllable-level POS template. The tree represents a floating word-level POS template constraint. Each path through the tree represents a POS sequence that is valid per the constraint. A transition is pruned from the NHMM if its syllable-level template, when identical consecutive tags are condensed, does not have a valid path through the tree. This is a floating dependency because the POS tags from the constraint are not imposed on specific positions in the syllable-level template. Thus despite having different syllable-level POS templates, both phrases satisfy the constraint via the same path (grey).
Table 1
d-order NHMMs with Floating and Dynamic Constraints for Solving the DBTB Problem.
| NHMM 1 | NHMM 2 | NHMM 3 | NHMM 4 | NHMM 5 | |
| NHM Order (d) | 4 | 5 | 5 | 6 | 8 |
| NHM Length (l) | 3 | 3 | 4 | 3 | 4 |
| Syllable Seq Length (n) | 6 | 7 | 8 | 8 | 11 |
| Rhythmic Template (r) | [011001] | [0110101] | [01010010] | [01101011] | [01010101010] |
| Training Sentences | 3,892,039 | 2,654,884 | 2,654,884 | 2,051,040 | 1,239,850 |
| Training Pronunciations | 366,062,046 | 286,075,704 | 286,075,704 | 255,086,072 | 208,330,754 |
| Solutions Generated | 30 | 5 | 5 | 4 | Not Satisfiable |
| Generated Example | “a dish of pickled fish” | “a cot and a chamber pot” | “a pillar that was a mirror” | “a mouse or a rat in the house” | n/a |
| Average Novelty | 3.65 | 3.66 | 4.13 | 3.40 | n/a |
| Average Rhyme | 4.18 | 4.21 | 1.94 | 4.00 | n/a |
| Average Rhythm | 3.12 | 3.30 | 2.13 | 3.16 | n/a |
| Average Amusement | 2.53 | 2.39 | 2.06 | 2.48 | n/a |
| Average Likability | 2.51 | 2.66 | 2.17 | 2.82 | n/a |
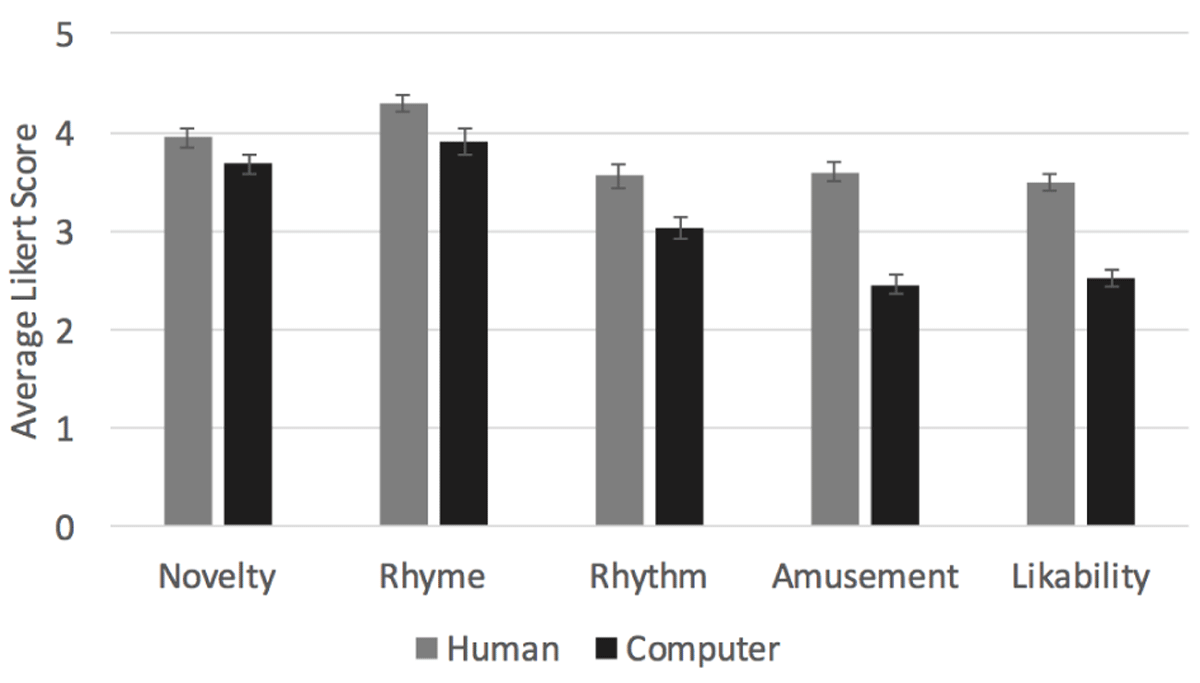
Figure 4
Qualitative evaluation. Results of 470 survey responses rating human- and computer-generated solutions to the DBTB problem. Error bars represent standard error.

Figure 5
Haikus. These haikus are generated from syllable-level NHMMs with floating dependencies. (Left) A haiku found using a 5th-order NHMM with a nature-themed floating semantic constraint. (Right) An original haiku generated from a 4th-order NHMM with floating word-level POS template constraints and a beauty/earth-themed floating semantic constraint.

Figure 6
Prosodic rhythm for lyrics. Given the lyric “No more monkeys jumping on the bed!”, we used a 4th-order NHMM over rhythm tokens to generate prosodic rhythms like those shown here. Stressed syllables are bold and notes in emphasized rhythmic positions are in parentheses.
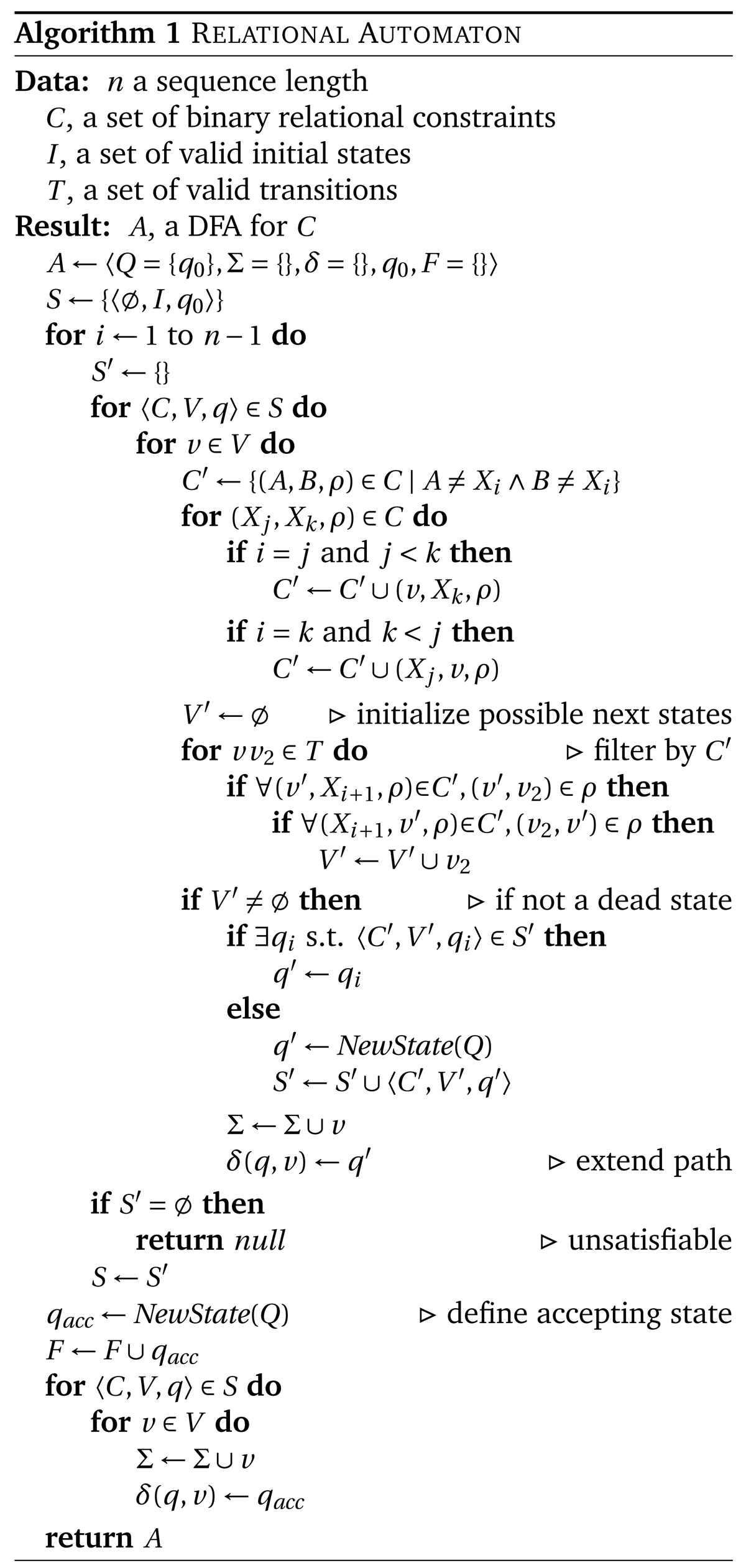
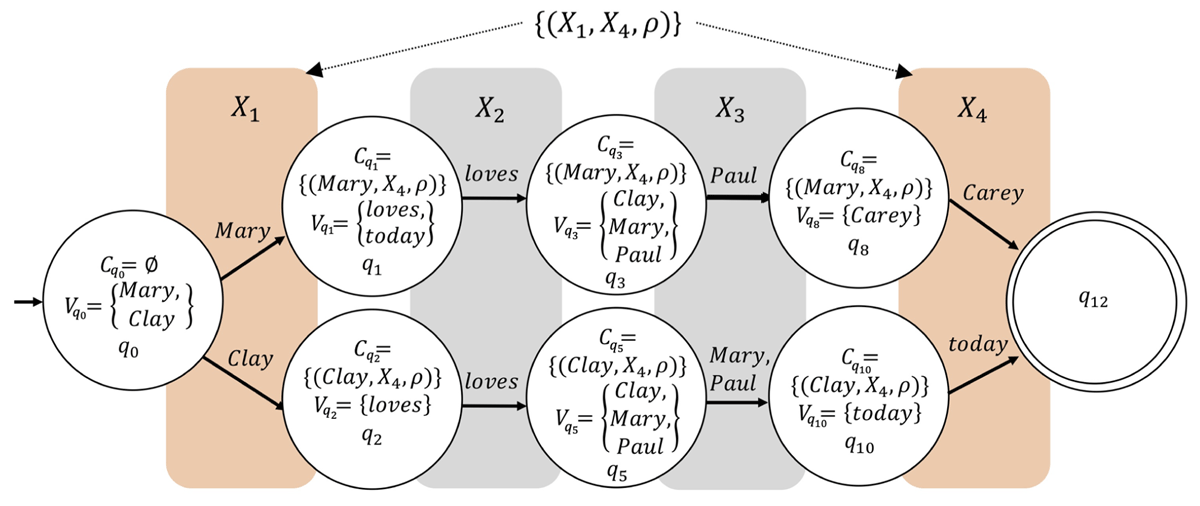
Figure 7
A Relational automaton. The result of Algorithm 1 on inputs n = 4; C = {(X1,X4,ρ)} (where ρ represents the set of all rhyming word pairs); I = {Mary, Clay}; and T derived from the non-zero transitions represented in the Markov model shown in Figure 8. Dead states and paths have been removed.
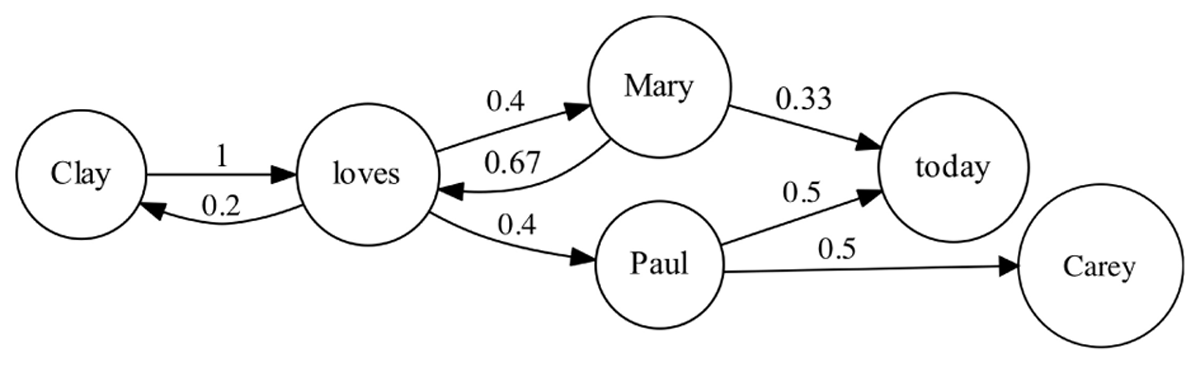
Figure 8
A Markov model. The model shown is a modified version of the model exemplified by Barbieri et al. (2012) to whom we pay tribute for having in large measure inspired this work. Missing is the initial probability distribution for the model which is Pi = {Mary, 0.5; Clay, 0.5}.

Figure 9
A “state-sensitive” pseudo-Markov model. This is the model M’ built using Algorithm 2 given as inputs the automaton in Figure 7, the Markov model in Figure 8, an empty unary constraint set, and a length n = 4. This is a “pseudo”-Markov model because, given this approach, probabilities must remain unnormalized for proper construction of the NHMM.

Figure 10
Sample Time By Length. Shown are average sample times for the NHMM (blue) and factor graph (orange) from sampling 100,000 sequences belonging to the set {aa + b+}. Both sample times increase linearly with the sequence length. Though the sample time per sequence is always lower for the NHMM, the NHMM build time also increases with sequence length resulting in a lower amortized sample time (dotted lines) for factor graphs as the sequence length increases.
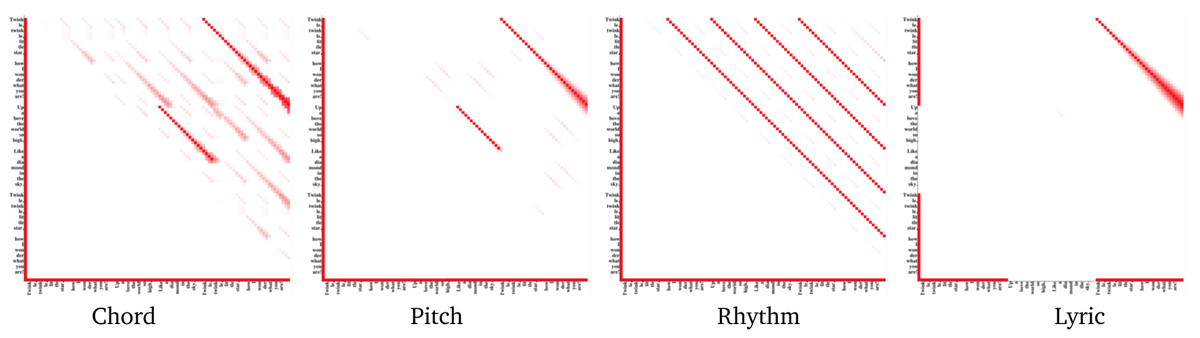
Figure 11
Inferring Relational Constraints. Relational constraint sets are inferred from real data using multiple-Smith-Waterman sequence alignment. Shown are the structural patterns inferred for the chord, pitch, rhythm, and lyric sequences in Twinkle, Twinkle, Little Star. The minute textual labels on the axes in each graph are the lyrics to the song and are merely a graphical reminder of what the axes represent.
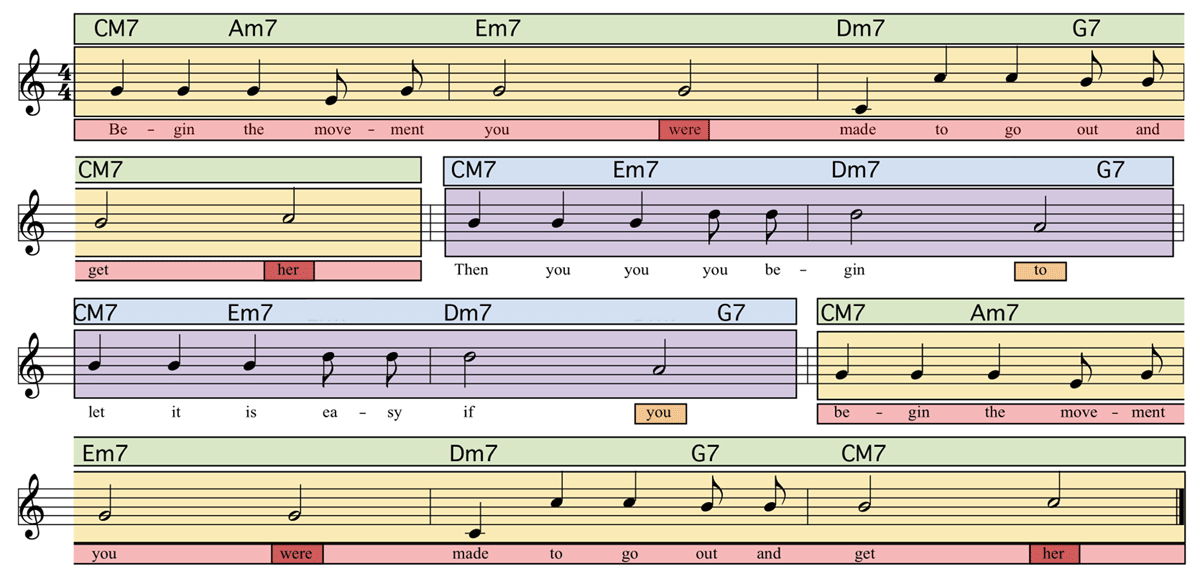
Figure 12
Composition generated with long-range dependencies. Shown are four parallel sequences (chords, pitches, rhythms, and lyrics) generated using Regular NHMMs that exhibit both local, horizontal structure—each fully satisfies Markovian constraints—and global, long-range structure—each fully satisfies binary relational constraints. Boxes of the same color are used to illustrate subsequences which position-by-position (e.g., eighth note by eighth note) are constrained via binary relational constraints to be equivalent. Dark red and dark yellow boxes reflect binary relational rhyming constraints. Not labeled is the pattern of rhythmic repetition every 2 measures.
Table 2
Long-range dependency constraints satisfied in generated compositions.
| Constraint Set 1 (Twinkle, Twinkle, Little Star) | Constraint Set 2 (Somewhere Over the Rainbow) | ||
| Form | Ternary (ABA) | 32-bar form (AABA) | |
| Measures | 12 | 32 | |
| Events per measure | 8 | 8 | |
| Composition length | 96 | 256 | |
| Total constraint count | Harmony | 48 | 64 |
| Rhythm | 16 | 96 | |
| Lyrics | 32 | 26 | |
| Pitch | 48 | 80 | |
| Rhyme | 3 | 7 | |
| Average constraint range (in eighth notes) | Harmony | 48 | 184 |
| Rhythm | 80 | 138 | |
| Lyrics | 64 | 192 | |
| Pitch | 48 | 160 | |
| Rhyme | 16 | 27 |
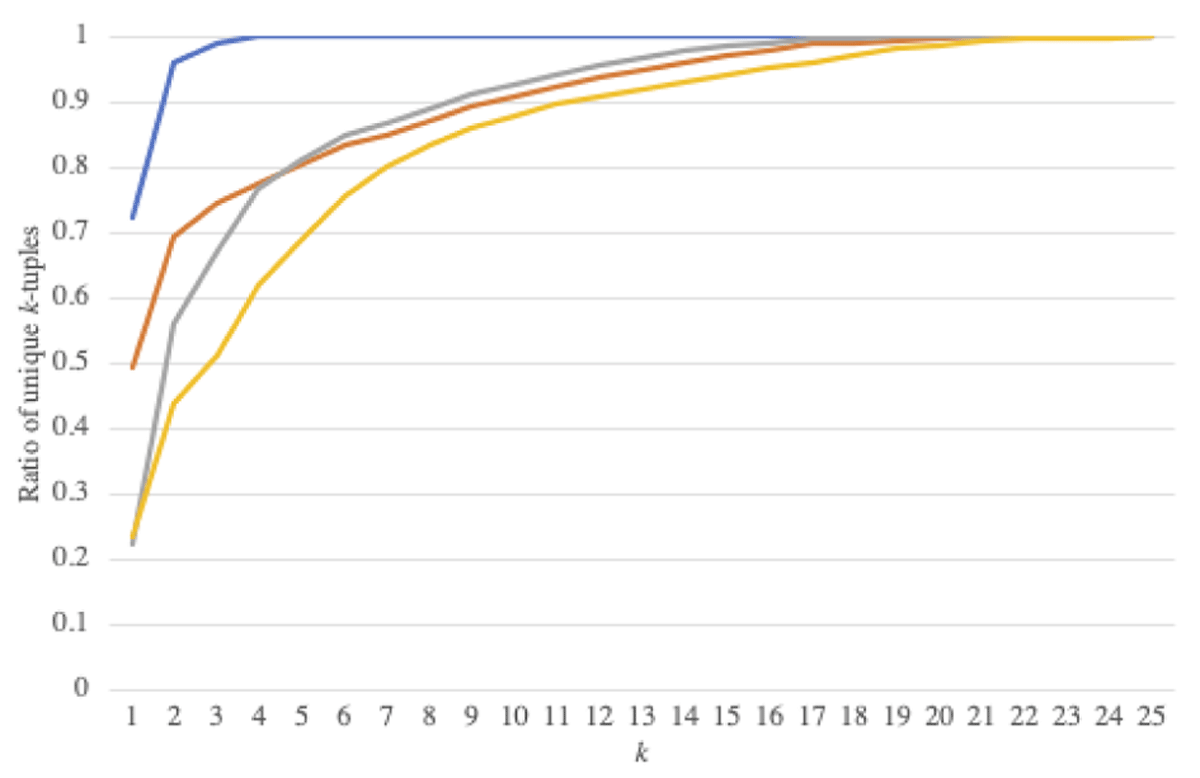
Figure 13
Variation in satisfying constraints. Though all 12 randomly selected compositions satisfy all specified constraints, they still remain highly varied in lyrics (blue), pitch (grey), harmony (red), and rhythm (orange). This is shown by considering that the ratio of k-tuples that are unique to one of the 12 compositions is high for even relatively small values of k. For lyrics, k is measured in words. For all other viewpoints, k is measured in eighth-note intervals (e.g., k = 8 represents one 4/4 measure). Compositions were normalized to a common key.

Figure 14
Variation in satisfying rhyme constraints. Of the 34 rhymes collectively incorporated into the 12 randomly selected compositions, all but one (94%) are unique and over a dozen different phonemic rhyming groups are represented.
