Fig. 1.

Fig. 2.

Fig. 3.

Fig. 4.
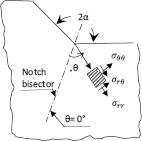
Fig. 5.
![Circular zone nears tip of V-notch [8], 2γ = 2π − 2α](https://sciendo-parsed.s3.eu-central-1.amazonaws.com/6509b809b429ff6411db0515/j_msp-2023-0027_fig_005.jpg?X-Amz-Algorithm=AWS4-HMAC-SHA256&X-Amz-Content-Sha256=UNSIGNED-PAYLOAD&X-Amz-Credential=AKIA6AP2G7AKOUXAVR44%2F20251204%2Feu-central-1%2Fs3%2Faws4_request&X-Amz-Date=20251204T144733Z&X-Amz-Expires=3600&X-Amz-Signature=63f6aa693ecdf8e8acff5dcd705768f33a8502ecd32c9ad020a034f281987a94&X-Amz-SignedHeaders=host&x-amz-checksum-mode=ENABLED&x-id=GetObject)
Fig. 6.
Fig. 7.

Fig. 8.

Fig. 9.
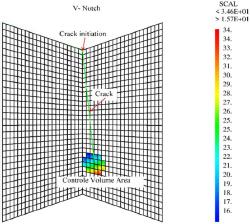
Fig. 10.
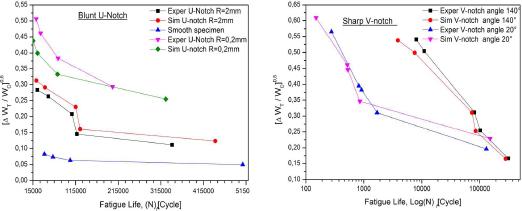
Fig. 11.
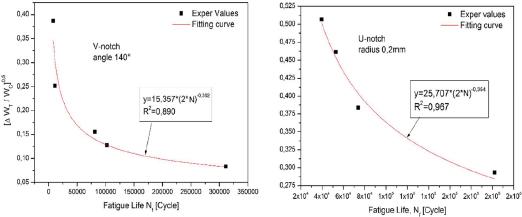
Fig. 12.
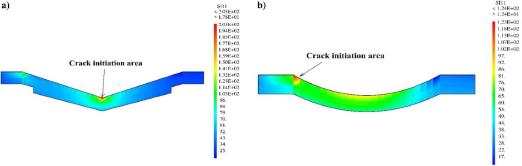
Fig. 13.

Fig. 14.

Fig. 15.

Correlations of experimental and numerical results
| Experimental test | |||||||
|---|---|---|---|---|---|---|---|
| Notch type | Number of test repetitions | Min. number of cycles | Max. number of cycles | Standard deviation of cycles | Minimum energy | Maximum energy | Standard deviation of energy |
| U-notch radius 0.2 mm | 4 | 22640 | 201,865 | 82391.597 | 0.293 | 0.507 | 0.094 |
| V-notch angle 20° | 4 | 521,218 | 151,883 | 75622.87 | 0.229 | 0.461 | 0.107 |
| V-notch angle 140° | 4 | 11032 | 311,170 | 129198.70 | 0.166 | 0.504 | 0.143 |
| U-notch radius 2 mm | 5 | 25,239 | 341,478 | 125086.76 | 0.112 | 0.283 | 0.074 |
| Simulation tests | |||||||
| Notch type | Number of test repetitions | Min number of cycles | Max number of cycles | Standard deviation of cycles | Minimum of energy | Maximum of energy | Standard deviation of energy |
| U-notch radius 0.2 mm | 4 | 15254 | 326,645 | 146,519.222 | 0.255 | 0.438 | 0.080 |
| V-notch angle 20° | 5 | 150.43 | 151,883 | 67,693.93 | 0.229 | 0.609 | 0.141 |
| V-notch angle 140° | 4 | 3890.97 | 85,337 | 42857.97 | 0.253 | 0.538 | 0.139 |
| U-notch radius 2 mm | 5 | 22938.2 | 442,920 | 169,677.83 | 0.124 | 0.313 | 0.081 |
Local energy modeling near notch
| Experimental | ||
|---|---|---|
| Notch type | Correlation coefficients | Experimental: Local energy near notch |
| U-notch radius 0.2 mm | R2 = 0.9881 | WU0.2 = 6,1122.(2N)-0.248 |
| V-notch angle 20° | R2 = 0.9591 | WV20 = 0,9019.(2N)-0.13 |
| V-notch angle 140° | R2 = 0.9656 | WU140 = 10,939.(2N )-0.325 |
| U-notch radius 2 mm | R2 = 0.8875 | WU2 = 14,731.(2N )-0.381 |
| Simulation | ||
| Notch type | Correlations coefficients | Simulation: Local energy near notch |
| U-notch radius 0.2 mm | R2 = 0.967 | WU0.2 = 25.707.(2N )-0.354 |
| V-notch angle 20° | R2 = 0.857 | WV20 = 1.944. (2N )-0.2093 |
| V-notch angle 140° | R2 = 0.890 | WU140 = 15.357.(2N )-0.392 |
| U-notch radius 2 mm | R2 = 0.8305 | WU2 = 12.483.(2N )-0.37 |
Mechanical properties of PMMA
| Tensile strength (MPa) | Flexural strength (MPa) | Modulus of elasticity (MPa) | Density (kg/m3) | Elongation (%) | Poisson’s rate | Fracture Toughness (MPa.√m) |
|---|---|---|---|---|---|---|
| 70.5 | 110 | 3000 | 1190 | 6 | 0.3 | 1.863 |