Breast cancer (BC) is an abnormal tumor that originates in the cells of breast tissue. It occurs when these cells begin to multiply uncontrollably, forming a tumor that can invade surrounding tissues or spread to other parts of the body [1], [2]. Although the exact causes of BC are not fully understood, numerous risk factors have been identified, including exposure to high levels of radiation [3]. Common symptoms of BC include skin wrinkles, nipple discharge, persistent breast pain, and the presence of a lump in the breast that may vary in size or shape. Each year, over 2.3 million new cases of BC are reported, making it the most common disease among women globally [4], [5]. Early detection and diagnosis significantly improve survival rates [6].
Medical imaging technologies are essential tools for detecting and diagnosing BC [7]. Machine learning (ML) [8], deep learning (DL) [9], and transfer learning (TL) [10] techniques have transformed the analysis of these imaging modalities, enabling accurate identification of cancerous tissues and differentiation between benign and malignant lesions. Convolutional neural networks (CNN) [11], recurrent neural networks (RNN) [12], and other DL algorithms [13] can automatically detect BC and improve diagnostic accuracy. The integration of DL methods in BC categorization improves diagnostic accuracy, reduces false positives, and supports personalized treatment strategies, ultimately advancing healthcare [7], [14]. The main contributions of this research are summarized as follows:
Introduces a novel TL-based tri-level classification network for BC stage classification, effectively handling both benign and malignant classes.
Utilizes ABCDE filtering to remove noisy artifacts and enhance the image quality for improved classification accuracy.
Incorporates an image augmentation phase to generate additional training data, improving the generalization of the network.
Employs the Golden Whale Optimization (GWO) algorithm, a hybrid of Golden-Eagle Optimization (GEO) and Whale Optimization (WHO) algorithms, to achieve precise lesion segmentation and improve detection performance.
The rest of this research is organized as follows. Section 2 reviews the existing works on breast cancer stage categorization. Section 3 presents the proposed model using histopathological images. Section 4 discusses the experimental results and appropriate interpretation of the findings. The conclusion of the proposed model is presented in Section 5.
Advancements in DL and ML have significantly improved BC detection and classification. This literature review highlights various methodologies, their strengths, and limitations in achieving precise and early BC diagnosis.
In 2024, Rahman et al. [15] developed a complex deep CNN that includes DL algorithms such as U-Net and YOLO for automatic recognition and localization of tumors in mammography images. This CNN achieved a high accuracy of 93.0 % using the publicly available MIAS dataset. In 2023, Abunasser et al. [16] used the ImageNet database to train five more specialized networks: InceptionV3, Xception, MobileNet, VGG16, and ResNet50. Each dataset was evaluated using these five pre-trained models along with the proposed DL model. This BCCNN approach achieved a categorization accuracy of 98.28 %.
In 2023, Raza et al. [17] developed DeepBreastCancerNet to distinguish BC. This system consists of 24 layers, including 6 convolutional layers, 9 inception modules, a fully connected layer, and various activation functions. The model achieved a maximum accuracy of 99.35 %. In 2023, Sharmin et al. [6] introduced a hybrid BC detection method that leverages a pretrained ResNet50V2 model along with ensemble-based ML techniques. This method combines the capabilities of DL and ML techniques to identify hidden patterns in complex BC images. The results provide compelling evidence that the hybrid model achieves an impressive accuracy rate exceeding 95 %.
In 2022, Reshma et al. [18] developed an autonomous segmentation technique for Fourier Transform-based separation in CAD systems and automatic morphological operation inputs. This approach improves speed and clarity for pathologists analyzing segmented images. In 2022, Singh et al. [19] designed a hybrid DNN that includes inception and residual blocks by combining multi-level feature maps. Image classification was conducted at multiple magnification levels. The proposed method achieved an accuracy of 96.42 % on the BreakHis dataset and 80.17 % on the BHI dataset.
In 2022, Liu et al. [20] introduced AlexNet-BC for classifying BC pathologies. AlexNet-BC was pre-trained with the ImageNet dataset and further trained with an enhanced dataset. The IDC and UCSB datasets further demonstrate its potential for extension, achieving accuracy rates of 86.31 % and 96.10 %, respectively. In 2022, Mohanakurup et al. [21] designed a composite dilated backbone network for BC detection on histopathological images. The lead backbone feature maps serve as the foundation for object identification in CDBN. These maps progressively supply the subsequent backbone with high-level output features from previous backbones. This CDBN resulted in mAP increases ranging from 1.5 % to 3.0 %.
In 2021, Hirra et al. [22] introduced Pa-DBN-BC to categorize the BC in histopathology images using DBN. Features were extracted from histopathology image patches through supervised fine-tuning and unsupervised pre-training phases, with classification performed using logistic regression. This approach was tested on a histopathology image dataset and achieved an accuracy of 86 %. In 2020, Hameed et al. [23] developed an ensemble DL method for accurately classifying BC into non-tumorous and tumorous categories. Five-fold cross-validation was conducted for each model: fully-trained VGG-16, fine-tuned VGG-16, fully-trained VGG-19, and fine-tuned VGG-19. The VGG networks achieved an overall accuracy of 95.29 % for the carcinoma class.
Despite their high accuracy, existing BC detection models have several limitations. Many rely heavily on pre-trained networks such as VGG16, ResNet, or Inception, which are not fully optimized for breast histopathology images and often require extensive fine-tuning. Additionally, most approaches focus on classification without addressing the need for early-stage detection or multi-stage cancer progression. Segmentation is often performed using traditional or semi-advanced methods, limiting precision in identifying lesions. Furthermore, some methods require complex architectural modifications or ensemble approaches, increasing computational cost and hindering real-time clinical applicability.
In this section, a novel TRI-BCC model is introduced, with a TL-based tri-level classification network for BC detection that effectively handles both benign and malignant cases. The overall schematic workflow of the proposed method is shown in Fig. 1.
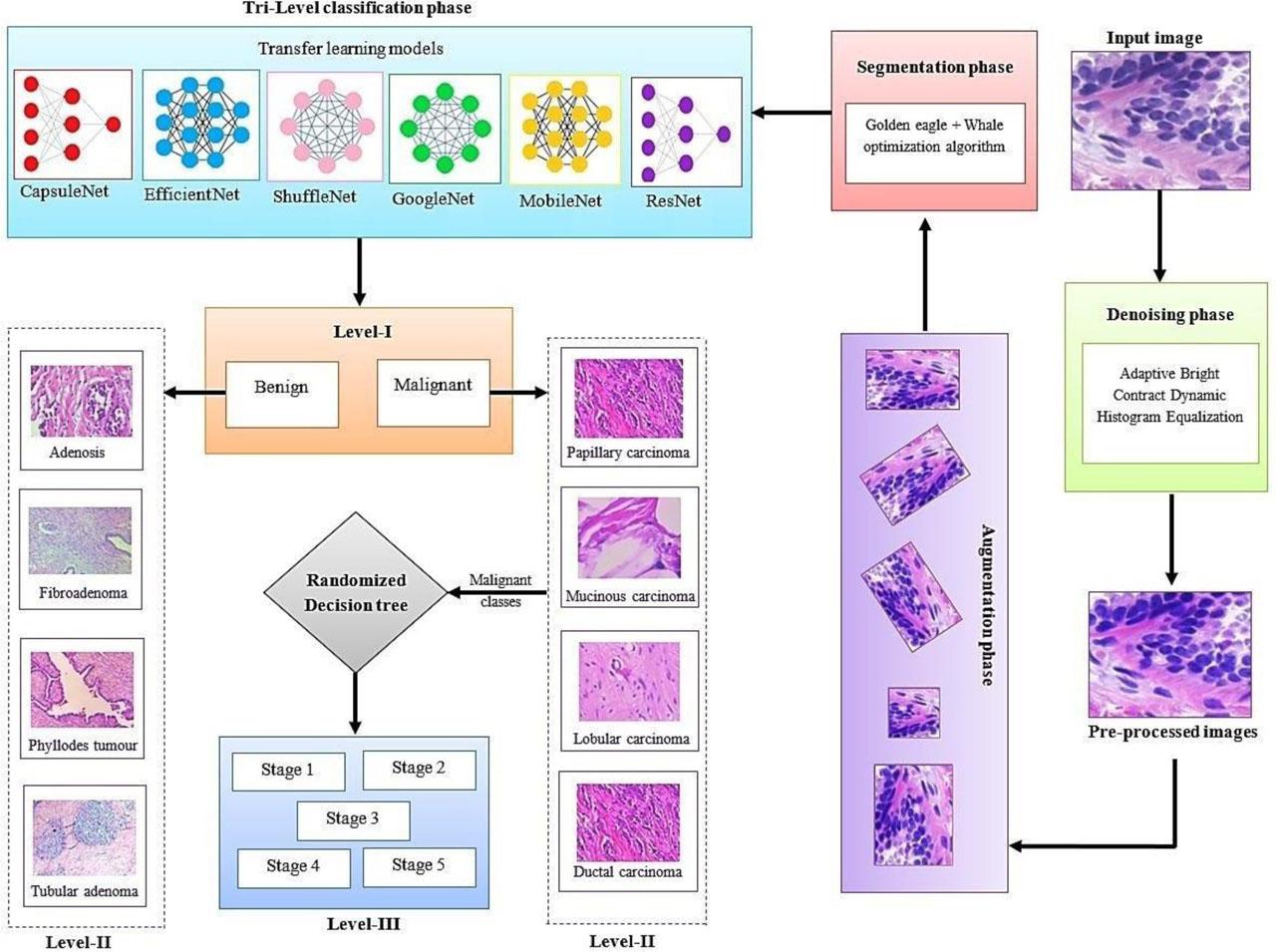
Schematic illustration of the proposed TRI-BCC model.
The BreakHis dataset is a benchmark dataset for BC recognition using histopathological images. It comprises 7909 images of breast tissue samples, divided into benign (2480) and malignant (5429) cases. The benign category includes subtypes such as Adenosis (AS), Fibroadenoma (FA), Phyllodes tumor (PT), and Tubular adenoma (TA). The malignant (5429) category includes subtypes such as Ductal carcinoma (DC), Lobular carcinoma (LC), Mucinous carcinoma (MC), and Papillary carcinoma (PC). These images are captured at four magnification levels to simulate real-world variability. The dataset supports both binary classification (benign vs. malignant) and multi-class classification for subtype identification. It presents challenges such as class imbalance and magnification variability, which can affect model performance. Table 1 provides a description of the BreakHis dataset with its different classes.
Dataset description of BreakHis with image count.
| Class type | Subtype | Image count |
|---|---|---|
| Benign | AS | 444 |
| FA | 1442 | |
| PT | 209 | |
| TA | 385 | |
| Malignant | DC | 3450 |
| LC | 626 | |
| MC | 792 | |
| PC | 561 | |
| Total | 7909 | |
Moreover, the malignant 5429 samples are manually annotated into five stages based on visual patterns observed in histopathological features. The stage-wise distribution was generated dynamically during the classification process rather than being pre-defined in the original dataset. These stage-wise labels are used internally to train the Randomized Decision Tree (RDT) for the final classification process. The stage-wise distribution of malignant subtypes is shown in Table 2.
Stage-wise distribution of malignant subtypes.
| Malignant subtype | Stage 1 | Stage 2 | Stage 3 | Stage 4 | Stage 5 | Total |
|---|---|---|---|---|---|---|
| DC | 460 | 790 | 970 | 670 | 560 | 3450 |
| LC | 110 | 160 | 140 | 110 | 106 | 626 |
| MC | 160 | 205 | 190 | 125 | 112 | 792 |
| PC | 105 | 130 | 145 | 90 | 91 | 561 |
| Total | 835 | 1285 | 1445 | 995 | 869 | 5429 |
Adaptive Brightness Contrast Dynamic Histogram Equalization (ABCDE) filtering is an image denoising and enhancement method that improves image contrast while minimizing noise. Histogram Equalization improves contrast by reallocating pixel intensities to utilize the full range of the image. The transformation function T(r) is defined in terms of the cumulative distribution function (CDF) of the image's intensity levels,
The sample size was increased using targeted augmentation techniques such as rotation, scaling, flipping, and zooming, which were selectively applied to underrepresented classes (benign subtypes) to address class imbalance and enhance dataset diversity. Rotation changes the image orientation, while flipping mirrors the images horizontally or vertically. Zooming involves enlarging or shrinking portions of an image, and scaling adjusts the image size. This targeted augmentation technique allows the model to train on a wider range of input images, reducing overfitting and improving sensitivity and predictive efficiency. For the experiment, all images were resized to a fixed 64×64 pixel resolution to extract RGB values as features. The dataset was then split into training (75 %) and testing (25 %) sets for further analysis of the proposed model.
Table 3 shows the class-wise image distribution in the dataset before and after targeted augmentation. The benign count increased from 2480 to 3680 when 1200 augmented images were added specifically to underrepresented benign classes. The final dataset comprises 9109 images, with 5429 images in the malignant class remaining unchanged to balance the dataset.
Augmentation count after targeted augmentation techniques.
| Class type | Subtype | Original count | Augmented count | Total count |
|---|---|---|---|---|
| Benign | AS | 444 | 400 | 844 |
| FA | 1442 | 0 | 1442 | |
| PT | 209 | 500 | 709 | |
| TA | 385 | 300 | 685 | |
| Subtotal | 2480 | 1200 | 3680 | |
| Malignant | DC | 3450 | 0 | 3450 |
| LC | 626 | 0 | 626 | |
| MC | 792 | 0 | 792 | |
| PC | 561 | 0 | 561 | |
| Subtotal | 5429 | 0 | 5429 | |
| Total | 7909 | 0 | 9109 | |
GWO algorithm is a hybrid of the GEO and WHO algorithm for efficient segmentation of histopathological images. This approach combines the global exploration strength of GEO with the local exploitation efficiency of the WHO algorithm, resulting in precise and accurate segmentation boundaries for histopathological images.
Fig. 2 illustrates the workflow of the proposed GWO algorithm for image segmentation. Initially, GEO performs a comprehensive global search, exploring diverse regions of the image to identify potential segmentation boundaries. Subsequently, WHO fine-tunes the identified regions using its spiral and encircling strategies, optimizing the segmentation boundaries with high precision.
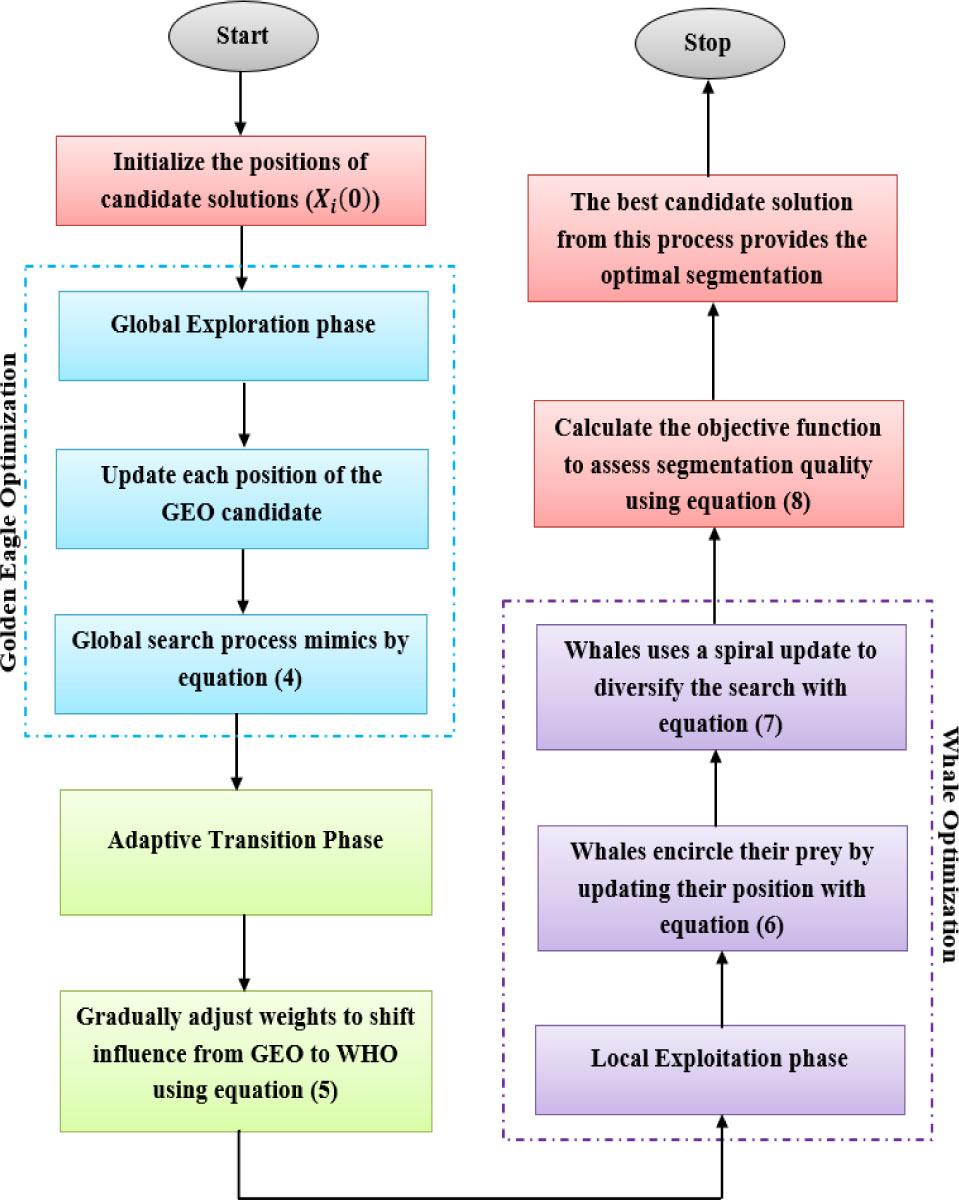
Flowchart of the proposed GWO algorithm.
Randomly initialize the positions of candidate solutions (boundaries) for histopathological image segmentation.
The GEO algorithm is inspired by the hunting behavior of golden eagles, which alternate between searching for prey from a distance (exploration) and swooping in on their target (exploitation). In GEO, the global search process mimics the broad area scanning of golden eagles looking for prey.
As the algorithm progresses, an adaptive switching mechanism gradually increases the influence of WHO while reducing the dominance of GEO. This transition ensures a smooth shift from broad exploration to focused exploitation. The adaptive weight formula is derived as,
In the final stages, the WHO algorithm fine-tunes the identified segmentation boundaries by exploiting the best-known solutions. The WHO algorithm incorporates mechanisms for both global search (exploration) and local search (exploitation) through two main strategies: encircling prey and spiral updating. The whales encircle their prey by updating their position relative to the best-known solution (Xbest):
The objective function for image segmentation was defined using metrics such as intra-class variance to minimize differences within segmented regions, boundary sharpness to precisely define cancerous and non-cancerous areas, and texture preservation to maintain important histological details in the images. The objective function for image segmentation is calculated as,
In this section, the tri-class classification in the proposed model involves three hierarchical levels for breast cancer diagnosis. In Level-I, the TRI-BCC differentiates between benign and malignant types. Level-II further classifies the benign and malignant classes into specific subtypes. Level-III focuses on staging malignant tumors (Stages 1 to 5) using a RDT. This stepwise classification improves diagnostic accuracy by combining TL models with structured staging, as is explained below.
CapsuleNet is designed to capture spatial hierarchies between features using capsules, where each group of neurons represents specific properties of the images. CapsuleNet replaces max-pooling with dynamic routing between capsules to preserve spatial relationships. The length of the capsule vector represents the prospect of the class. Given input xi to a capsule, the output capsule zi is,
EfficientNet relies on the use of reversed bottleneck MBConv. This structure has depth-separable convolutions instead of conventional layers, achieving nearly a k2 factor, where ks indicates the kernel size representing the height and width of the convolutional layers. The activation function in EfficientNet is ReLU. In compound scaling, the compound coefficient μ is applied, and the following rules are derived:
In (10), the constant variables α,β,γ≥1 are determined based on the compound coefficient μ through grid search. The computational complexity in the convolutional block depends on attributes such as 𝔻, 𝕎2, and ℝ2ν, which contribute to processing in the convolution layers. As the network expands around (α, β2, γ2)φ and (α β2γ2)φ, as shown in (10), the total computational workload of EfficientNet increases. Despite the higher computational burden, using α,β,γ enables faster retrieval of neural features from larger models.
ShuffleNet is a lightweight CNN designed for low-computation environments. It uses grouped convolutions and channel shuffling to minimize the number of parameters while maintaining efficacy in BC detection. The grouped convolution divides channels into small groups to reduce computation, and channel shuffling ensures information exchange between groups. The resultant feature map Y of a group convolutional layer is,
GoogleNet, also known as Inception-v1, uses Inception units that allow the network to capture patterns at various scales, making it suitable for histopathological images with both small and large tissue structures. In the Inception module, each block applies 1×1, 3×3, and 5×5 convolutional layers in parallel, followed by concatenation of the results. Global average pooling reduces overfitting by averaging the feature map instead of using dense layers. The inception module is defined as,
MobileNet is a lightweight DL network developed for mobile and embedded devices. It was designed with depth-wise separable convolutions to reduce the number of parameters while preserving accuracy. The Depth-wise Separable Convolution layer is split into a depth-wise convolution and a point-wise convolutional layer.
ResNet-101 is a deep network that uses residual connections to address the disappearing gradient problem by permitting the network to learn very deep representations. This is essential for detecting subtle features in large histopathological datasets. Each residual block learns a residual function instead of a direct mapping, making optimization easier. The depth of the network allows it to capture intricate patterns in cancerous tissue.
In the context of final stage classification, the RDT is used to predict malignant cancer stages from Stage 1 to 5 based on histopathological features such as cell structure, nuclei shape, size, mitotic count, and tissue patterns. The RDT is a variant of the traditional Decision Tree algorithm that introduces randomness in the splitting criteria. After classifying the BC subtypes, the RDT determines the cancer stage (Stage 1 to 5). The main idea is to build a tree that randomly selects a subset of features (rather than all features) at each split. This randomness reduces the risk of overfitting and allows the tree to explore multiple splitting strategies. The Gini impurity calculates the prospect that a randomly selected sample would be inaccurately recognized if labels were assigned randomly, reflecting the distribution of labels at a given node. This is used to evaluate the quality of a split.
This section uses Matlab-2020b to implement the experimental results and assess the efficiency of the proposed model. For this experiment, the collected datasets are used as the retrieval dataset, with 75 % used for training and 25 % used for testing. The experimental results of the proposed model use a sample of collected dataset images are visualized in Fig. 3.
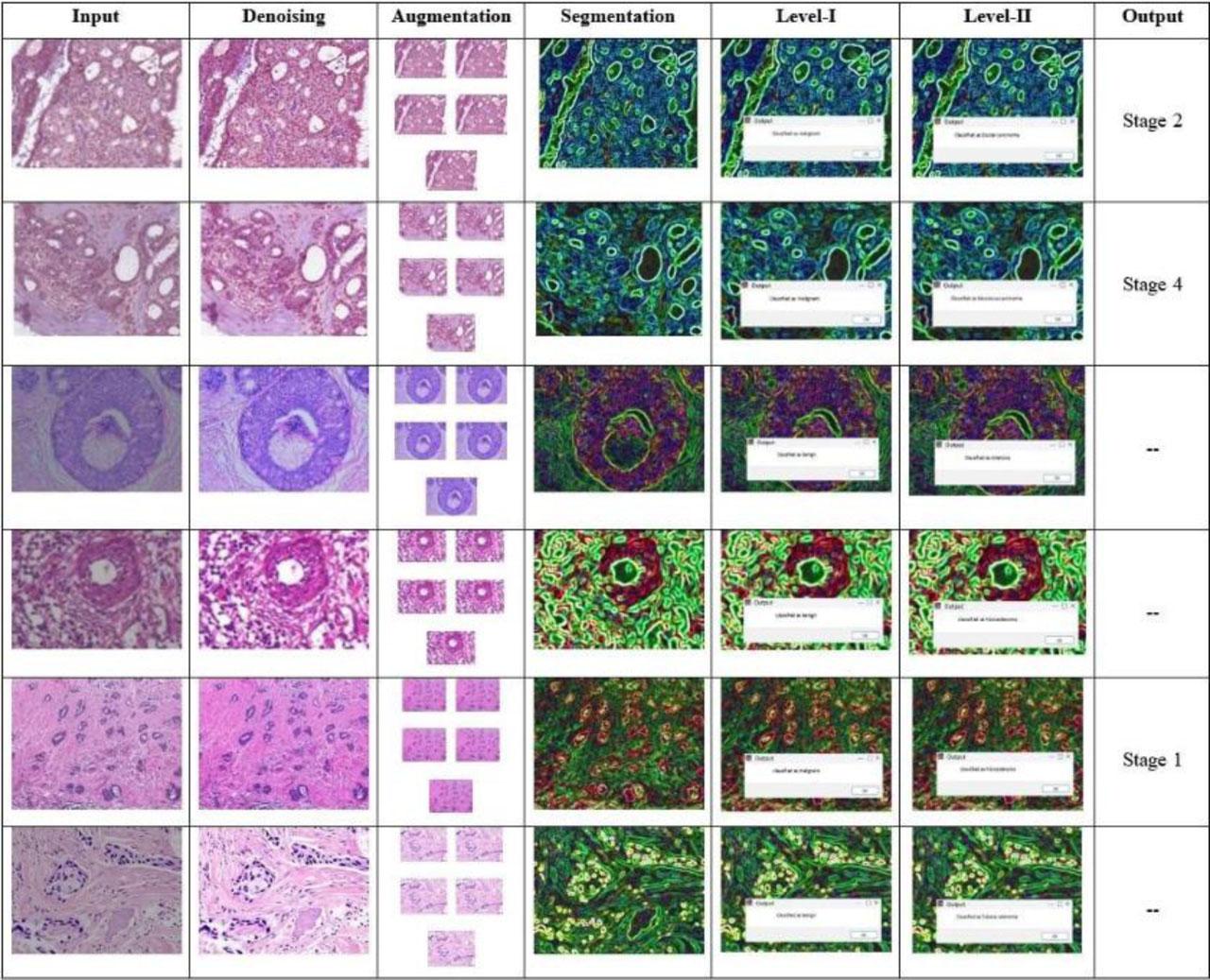
Experimental results of the proposed TRI-BCC model for BC classification.
Fig. 3 shows a tri-level classification process for BC analysis from collected images. The process starts with input histology images (colum 1), followed by denoising to enhance image clarity (column 2). Augmentation is performed to increase data variability (column 3). The images are then segmented to identify key regions within tissue structures (column 4). Level-I identifies the general category, such as benign or malignant (column 5), while Level-II identifies the specific classes of benign and malignant (column 6). The final output column shows the classified cancer stage of malignant cases (column 7).
In this section, several performance evaluation metrics, including specificity (SPE), sensitivity (SEN), precision (PRE), accuracy (ACC), and F1 score (F1S), are employed to objectively assess the proposed approach. Additionally, the Dice score (DS) and Jaccard score (JS) are also used for further segmentation evaluation.
Table 4 summarizes the performance of BC recognition in distinguishing between benign and malignant tumors (Level-I). The ACC is slightly higher for benign cases (99.25 %) than for malignant cases (98.84 %). The SPE is higher for benign cases (99.01 %), reflecting better false-negative avoidance. SEN shows that malignant tumors are detected more often (99.01 %) than benign tumors (98.73 %). The PRE value is higher for malignant cases (99.27 %) compared to benign cases (98.45 %), indicating fewer false positives. F1S indicates better balance in malignant detection (99.49 %) compared to benign detection (98.18 %).
Efficiency analysis of the proposed TRI-BCC model for Level-I.
| Classes | ACC | SPE | SEN | PRE | F1S |
|---|---|---|---|---|---|
| Benign | 99.25 | 99.01 | 98.73 | 98.45 | 98.18 |
| Malignant | 98.84 | 98.06 | 99.01 | 99.27 | 99.49 |
| Average | 99.04 | 98.95 | 98.69 | 99.49 | 98.47 |
Fig. 4 compares the performance metrics across various benign and malignant classes. Among benign classes, the FA subtype has the highest overall performance, while the TA subtype shows relatively lower scores. In malignant classes, the PC subtype demonstrates strong sensitivity and F1 scores, whereas the MC subtype performs relatively lower across all metrics. These graphs highlight the superior efficiency of the proposed TRI-BCC for classifying various BC subtypes.
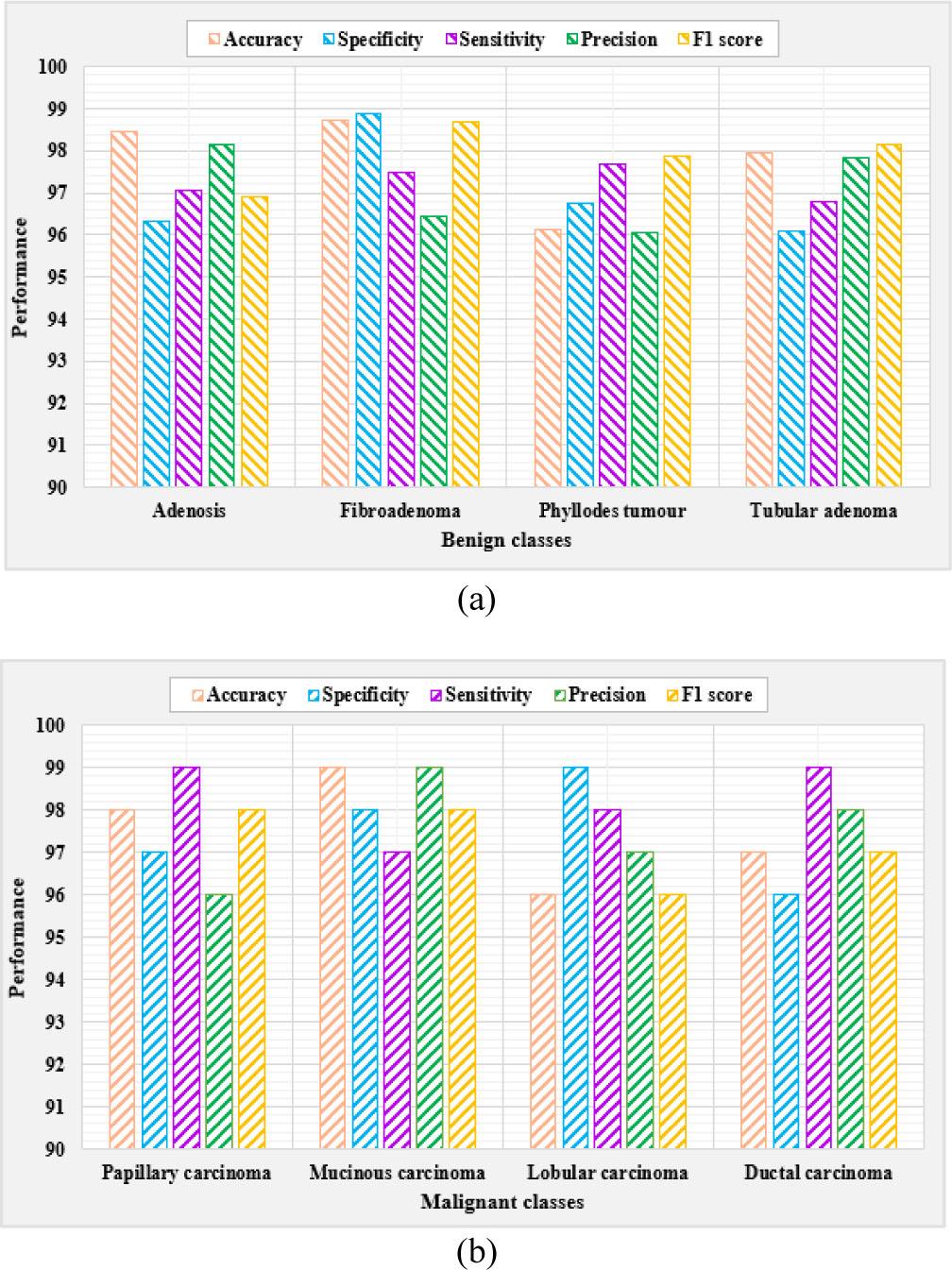
Level-II analysis of the proposed TRI-BCC model for (a) Benign classes and (b) Malignant classes.
Fig. 5 illustrates the performance of the breast cancer detection model across malignant stages (Stage 1 to 5) by showing trends in performance metrics. Stage 4 exhibits a notable drop in specificity, while other metrics remain relatively stable across stages. Precision peaks at Stage 2 and drops at Stage 4, whereas sensitivity shows an increasing trend after Stage 1. The F1 score remains consistent, reflecting balanced performance particularly at Stage 5.
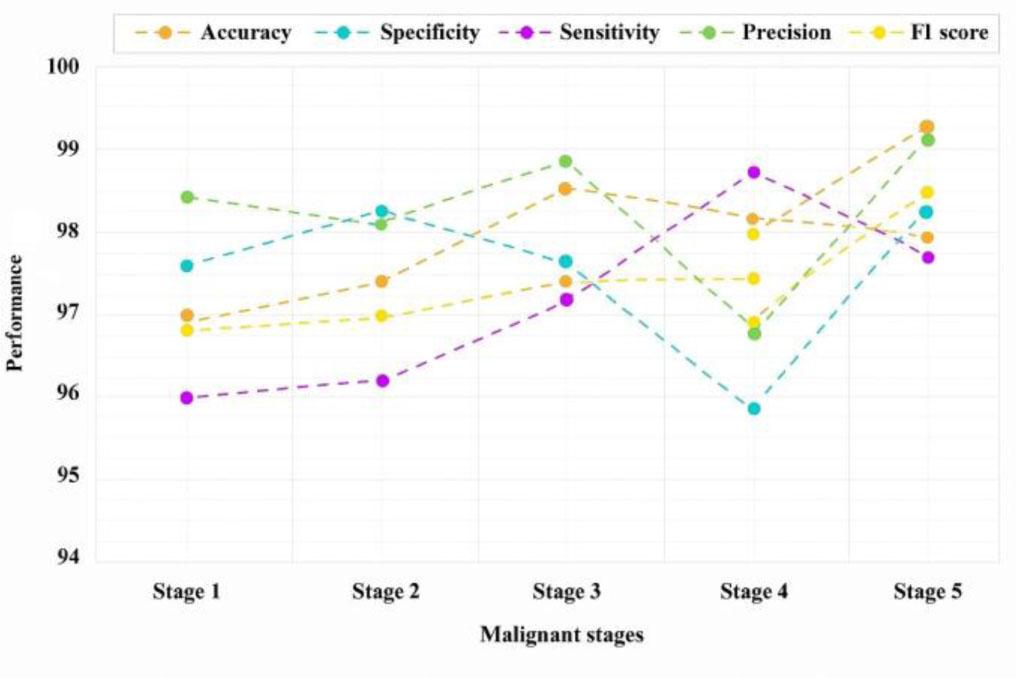
Level-III analysis of the proposed TRI-BCC model for Malignant class stages.
The accuracy curve in Fig. 6(a) was generated over 100 epochs at a specified reliability level. Similarly, Fig. 6(b) shows the epochs and loss curve, showing the minimal loss assessed for the proposed model as the number of epochs increases. These findings demonstrate the efficiency of the proposed TRI-BCC model for classifying BC stages with a low error rate.
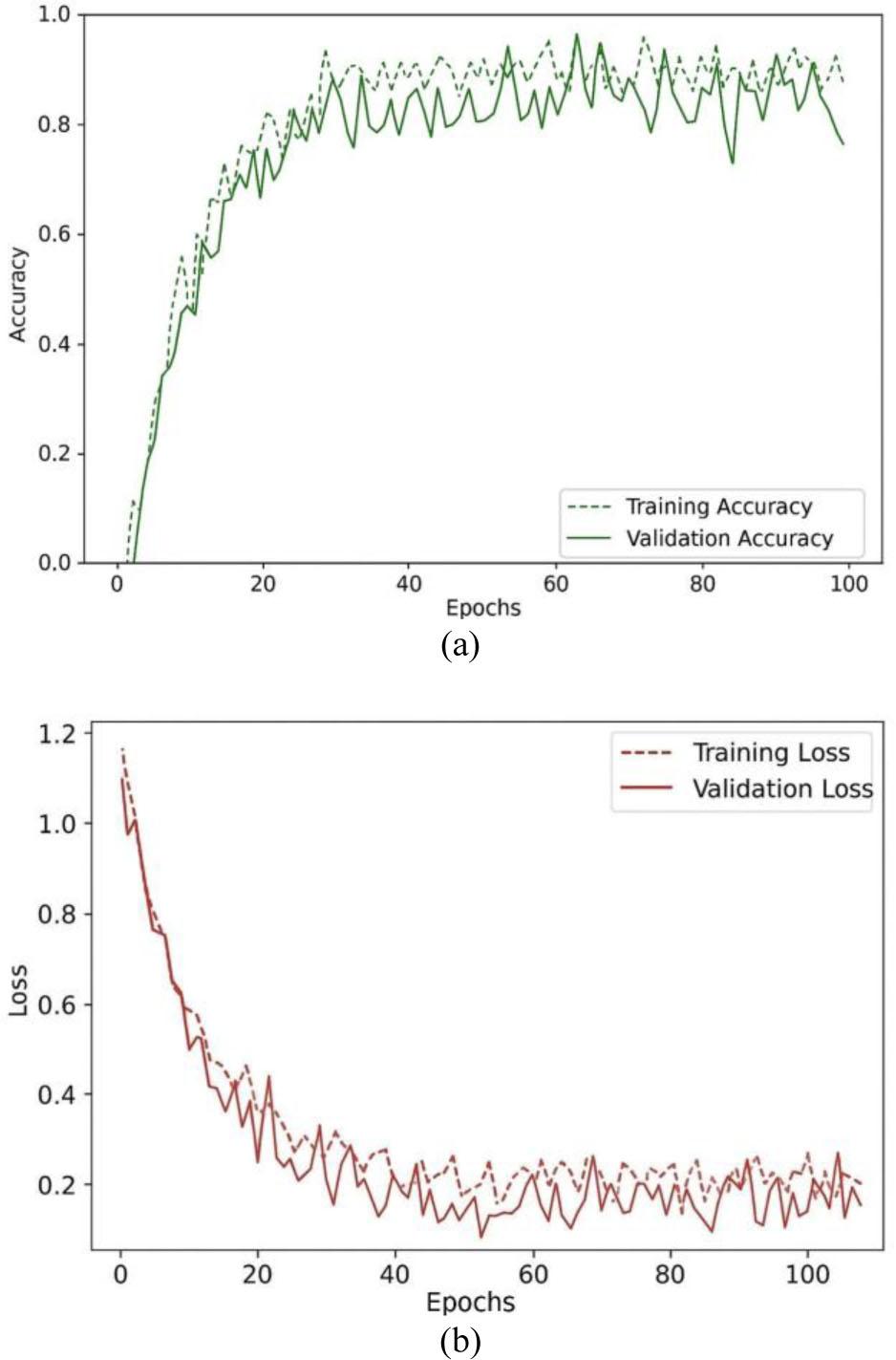
Training and testing curve of the proposed TRI-BCC model (a) Accuracy curve; (b) Loss curve.
In this section, the proposed TRI-BCC framework was evaluated alongside existing BC classification models using various metrics. The TRI-BCC model was evaluated against other DL structures with multiple measures.
Table 5 compares the performance of three existing models: Firefly Optimization (FFO), Aquila Optimization (AO), and Bald Eagle Search Optimization (BESO), based on two key segmentation metrics: DS and JS. Both metrics measure the overlap between predicted and actual segmentation, with higher values indicating better efficiency. The proposed GWO algorithm outperforms the others by achieving the highest DS (0.91) and JS (0.87), indicating improved segmentation accuracy.
Comparative analysis of optimization algorithms based on DS and JS.
| Metrics | FFO [24] | AO [25] | BESO [26] | GWO (ours) |
|---|---|---|---|---|
| Dice score | 0.82 | 0.85 | 0.87 | 0.91 |
| Jaccard score | 0.76 | 0.79 | 0.81 | 0.87 |
Table 6 compares the efficiency of various classification methods for a particular dataset using ACC, SPE, SEN, PRE, and F1S. Random Forest (RF) demonstrates the highest overall performance, with an accuracy of 96.3 % and strong precision, sensitivity, and specificity. K-Nearest Neighbors (KNN) also performs well, particularly in sensitivity (95.5 %). Decision Tree (DT) and Naive Bayes (NB) show moderate results, with accuracies of 89.5 % and 87.9 %, respectively. The RDT model achieves a balanced performance across all metrics.
Comparative evaluation of different ML classification models.
| Methods | ACC | SPE | SEN | PRE | F1S |
|---|---|---|---|---|---|
| NB | 87.9 | 86.8 | 88.4 | 86.3 | 87.2 |
| DT | 94.7 | 94.0 | 95.5 | 93.1 | 94.2 |
| RF | 96.3 | 95.9 | 96.8 | 95.4 | 96.1 |
| KNN | 89.5 | 89.0 | 90.2 | 88.7 | 89.1 |
| RDT | 99.04 | 98.9 | 98.6 | 99.4 | 98.4 |
Fig. 7 presents a comparison of segmentation methods applied to histopathology images. The first column displays the original input images, followed by the ground truth segmentation. The subsequent columns show results from various segmentation techniques: FFO [24], AO [25], and BESO [26] algorithms, along with the proposed GWO algorithm. The GWO algorithm produces clearer and more accurate segmentation results by closely aligning with the ground truth, indicating its effectiveness over other techniques.
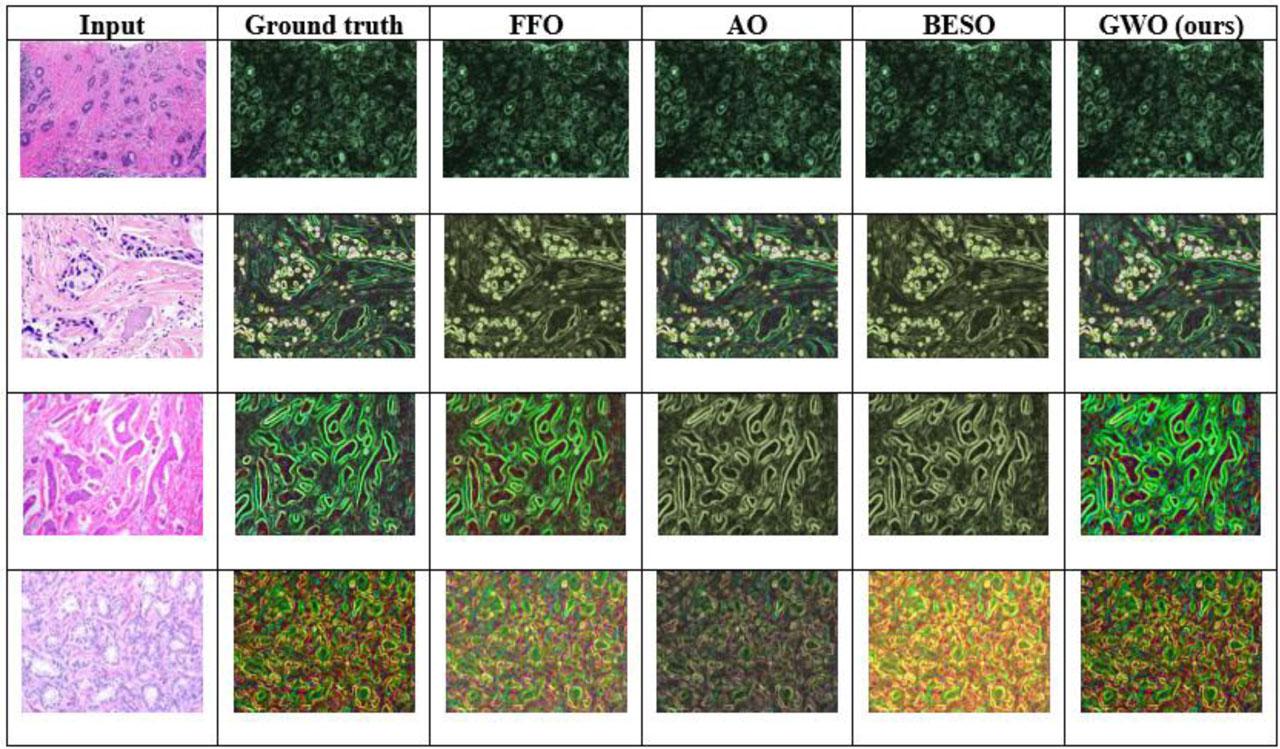
Visual comparison of different optimization algorithms for segmentation.
Table 7 compares various methods for a specific task based on their accuracy rates. The combination of U-Net and YOLO achieves 93.0 % accuracy, while the fine-tuned networks yield an accuracy of 98.28 %. The hybrid deep neural network achieves 96.42 % accuracy, and the Pa-DBN-BC model has the lowest accuracy at 86.0 %. The proposed TRI-BCC model achieves the highest accuracy of 99.06 %, indicating its superior efficiency over previous methods. The proposed TRI-BCC model improves overall accuracy by 6.11 %, 0.78 %, 2.66 %, and 13.18 % compared to U-Net + YOLO, fine-tuned networks, hybrid deep neural network, and Pa-DBN-BC, respectively. This analysis highlights the progression of accuracy improvements with each approach, demonstrating the effectiveness of the proposed TRI-BCC model.
Accuracy comparison: proposed model vs existing models.
| Authors | Methods | Accuracy |
|---|---|---|
| Rahman et al. | U-Net + YOLO | 93.00 % |
| Abunasser et al. | Fine-tuned networks | 98.28 % |
| Singh et al. | Hybrid deep neural network | 96.42 % |
| Hirra et al. | Pa-DBN-BC | 86.00 % |
| Proposed model | TRI-BCC model | 99.06 % |
This work introduces the TRI-BCC model, a highly accurate and efficient approach for classifying BC stages using a tri-level classification framework. Histopathological images are enhanced through ABCDE filtering, followed by optimized segmentation using the GWO algorithm. The TL models include CapsuleNet, EfficientNet, ShuffleNet, GoogleNet, MobileNet, and ResNet to classify cases into benign and malignant categories. Identified benign and malignant conditions undergo further staging using RDT to classify cancer into five distinct stages. The proposed TRI-BCC model demonstrates higher efficiency in classifying benign and malignant cases and further categorizing cancer stages. The competence of the proposed TRI-BCC model was assessed using ACC, SPE, SEN, PRE, F1S, DS, and JS. The proposed TRI-BCC model outperforms current techniques, achieving an accuracy of 99.06 %, making it an efficient tool for improving early detection. The proposed TRI-BCC model improves overall accuracy by 6.11 %, 0.78 %, 2.66 %, and 13.18 % compared to U-Net + YOLO, fine-tuned networks, hybrid deep neural network, and Pa-DBN-BC, respectively. Future work could involve developing custom DL architectures specifically tailored to histopathological image features and exploring hybrid optimization techniques to enhance segmentation accuracy in complex and noisy datasets.