The success of fashion brands depends on selling products that are adopted by the mass consumers during a particular period [1].To achieve this goal, designers mostly rely on their own experience to guess consumers’ preferences. However, designers’ unilateral experience and ideas may not align with consumers’ demands. Therefore, the design and sale of clothing products are confronted with the key issues of how to identify users’ real needs and how to meet their preferences.
The value of high-end clothing is constructed through the interaction between designers and consumers [2]. During the process of clothing design, the interaction between designers and consumers should be taken into consideration to ensure the appeal of the products to consumers. Consumers’ preferences serve as a crucial dimension in describing the product style and its psychological experience [3]. Consumer preference data can directly reflect the degree of consumers’ recognition of a certain product and is also an important indicator for predicting the effectiveness of product design [4]. In modern design oriented towards consumer demands, how to effectively integrate product design with user preferences has become a core issue in market competition.
In the field of design, consumer preference research has become a topic of concern. Scholars have extensively explored consumer preferences across various design disciplines, including architecture [5–6], product design [7–8], furniture design [9], and interaction design [10–11]. In the research of fashion design, fashion innovation technologies have also emerged [12]. Interdisciplinary research has provided new methods for fashion design. Specifically, factors such as user behavior in online shopping environments [13], key considerations during virtual try-on experiences [14], and the integration of user preferences into recommendation algorithms, collectively provide new and up-to-date ideas for fashion design [15–16].
In the field of perception in fashion design, some researchers have explored the styles and attributes preferred by consumers through quantitative methods and established fashion design models to meet consumers’ style preferences [17–18]. Consumer attitudes and expectations regarding clothing design have received significant scholarly attention [19–20]. To address this, a personality assessment scale tailored to the fashion industry has been developed [21], and key factors influencing user evaluations of fashion products have been presented in research [22].
Variations in clothing design elements generate diverse aesthetic outcomes. In the selection of clothing elements, different user groups show preference differences for design elements such as silhouette and color [23–24]. By analyzing the relationship between clothing design factors, aesthetic experience and preferences, the quality of clothing design can be improved [25]. For example, Ko proposed a method for designing protective clothing with better working performance [26], and Zhou used conjoint analysis to establish a combination of dress elements based on consumer preferences [27].
The above-mentioned research investigated the relationship between consumer preferences and the style and design elements of clothing, providing methods for the style positioning and detailed design of clothing. However, a clothing design scheme is formed by the combination of multiple design features. Current research primarily focuses on the analysis of clothing style attributes and individual design elements, making it challenging to apply these findings to comprehensive design schemes that integrate multiple design features. Therefore, the challenge lies in how to select key design features and optimize their combinations to create an integrated design that aligns with user preferences.
As the primary category of men’s formal wear, the overall visual effect of a suit is influenced by a variety of design elements. However, existing research on suit design predominantly focuses on collar styles [28–29]. In this study, to enhance consumers’ emotional preference for clothing products, an integrated algorithm combining a BP neural network and genetic algorithm is employed to propose an optimization method for clothing design. This approach facilitates user-centered design and enables the generation of clothing schemes that align with consumer preferences.
The appearance of a man’s suit is influenced by various design elements. In this study, we selected key design elements from three aspects: fabric pattern, main color, and style design. The rationale and procedures for selecting these design elements and their associated design features are detailed in reference [30]. Table 1 presents the design elements selected in this paper and their corresponding design features.
Illustrations of design elements and features of a men’s suit
| Attribute (Design element) | Level (Design feature) |
|---|---|
| FABRIC(A) | |
| COLOR(B) | |
| SILHOUETTE (C) | |
| COLLAR OPENING (D) | |
| BOTTOM HEM (E) | |
| COLLAR TYPE (F) | |
| WAIST POCKET (G) |
Suit samples can be generated through various combinations of the aforementioned design features. Given the number of design features outlined in the previous section, there were a total of 2,187 possible design combinations, a number too large for participants to evaluate within the scope of the experiment. To ensure experimental reliability, we employed the orthogonal design method to select representative suit samples. The style diagrams of the 16 samples selected are presented in Figure 1.

Illustration of suit samples
In this experiment, participants were instructed to evaluate the 16 suit samples based on their personal preferences. The item “disliking–liking” was assessed using a five-point Likert scale, where −2 indicated “totally dislike” and +2 represented “totally like.” The survey was distributed through a professional research platform. A total of 687 male consumers participated in the study.
In order to build the BP neural network model of suit design features and consumer preference, the input vector of training samples includes the values of a total of 21 design features under 7 design elements for each sample, and the output vector is the average value of consumer preference experiments for each sample.
A three-level structure consisting of an input layer, single hidden layer, and output layer was employed to construct a BP neural network model that relates suit design features to consumer preferences. The input layer contains 21 neurons, while the output layer consists of a single neuron. It was determined that the root-mean-square error (RMSE) was minimized when the number of neurons in the hidden layer was set to half the total number of neurons in the input and output layers [31]. Therefore, the hidden layer was configured with 11 neurons, which proved to be an optimal and effective configuration during subsequent neural network operations. The final BP neural network architecture is illustrated in Figure 2.
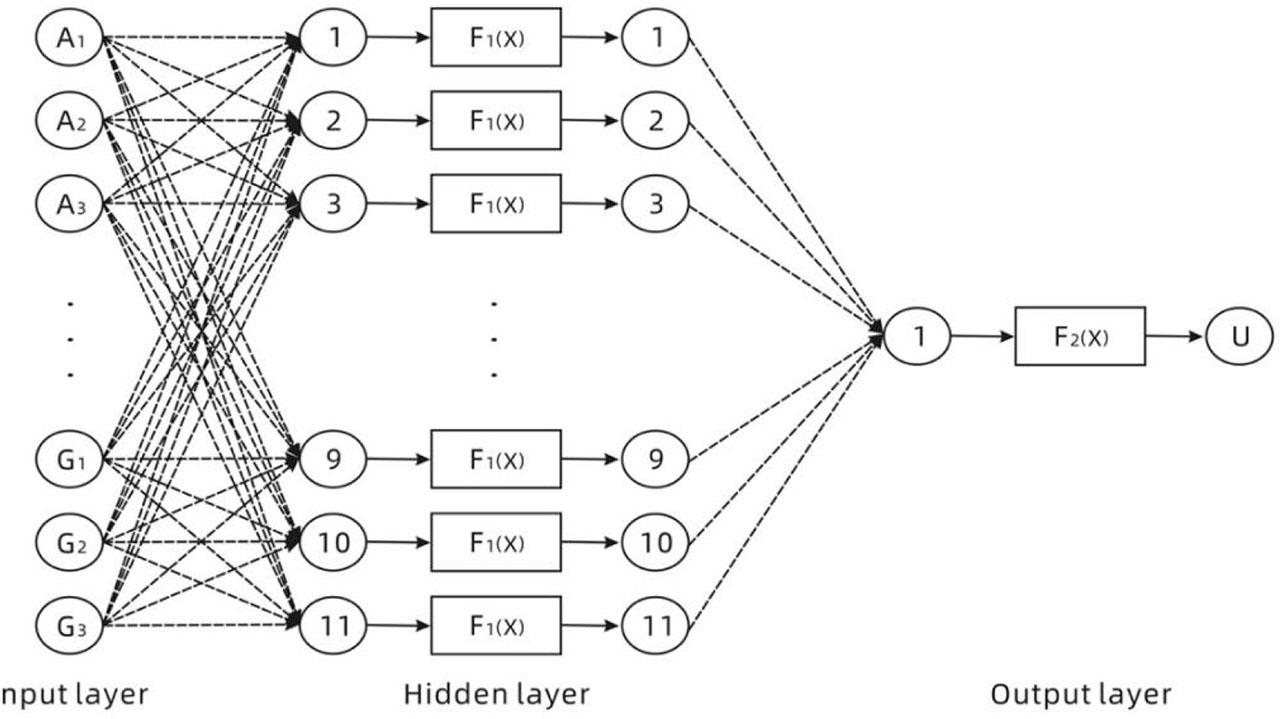
BP neural network structure
A BP neural network model that relates suit design features to consumer preferences was developed using MATLAB software. In this model, the corresponding output vector can be predicted once the input vector is provided. Specifically, the training data consisted of 21 suit design features and the average scores of consumer preferences. The BP neural network was configured with the TRAINLM training function, and the Levenberg-Marquardt algorithm was employed for network learning. The maximum number of training epochs was set to 1000, with a training target of 10%. After four training iterations to adjust the weights, the final error accuracy reached 1.19×10−11, which was significantly lower than the preset threshold of 10%, leading to the termination of the training process. The resulting model parameters are presented in Figure 3, and the corresponding error curve is illustrated in Figure 4.
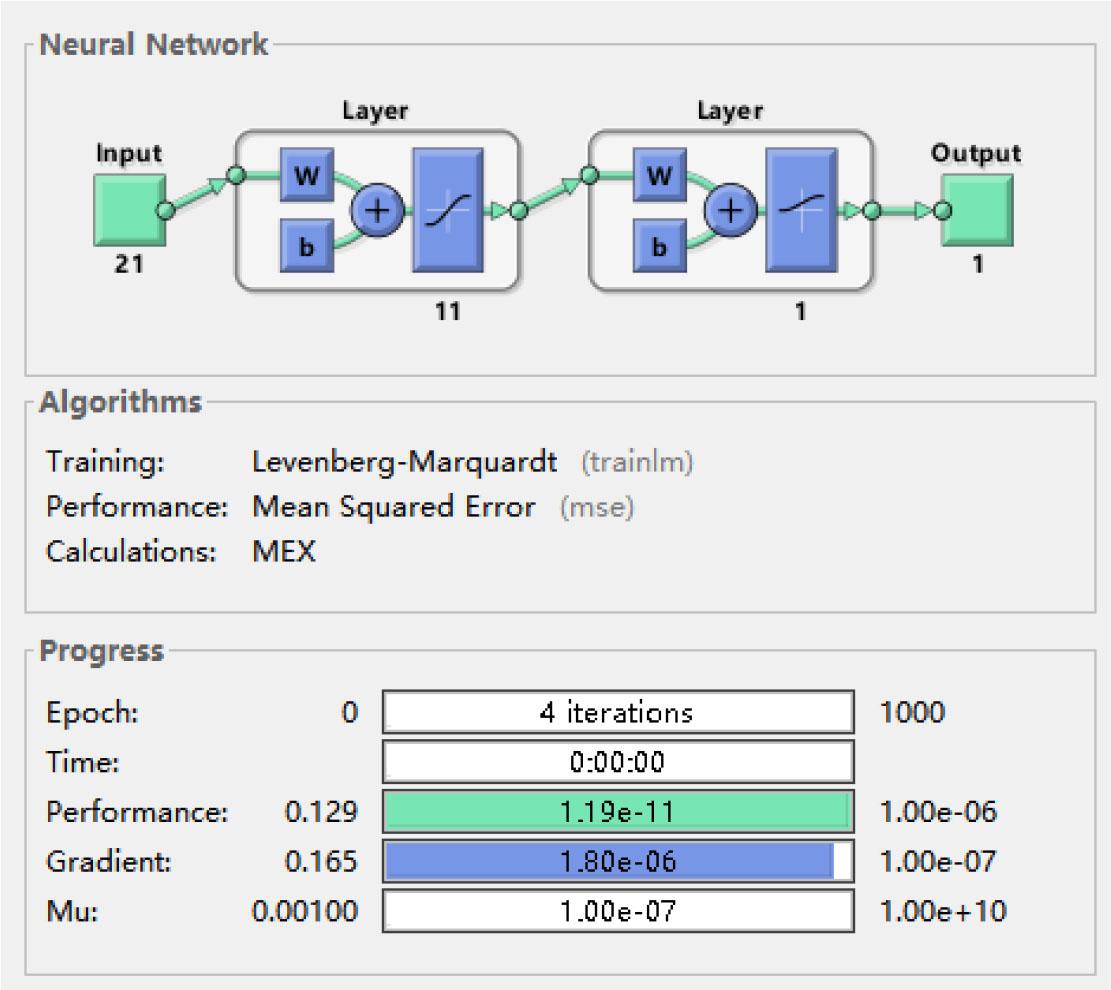
Result parameters of BP neural network
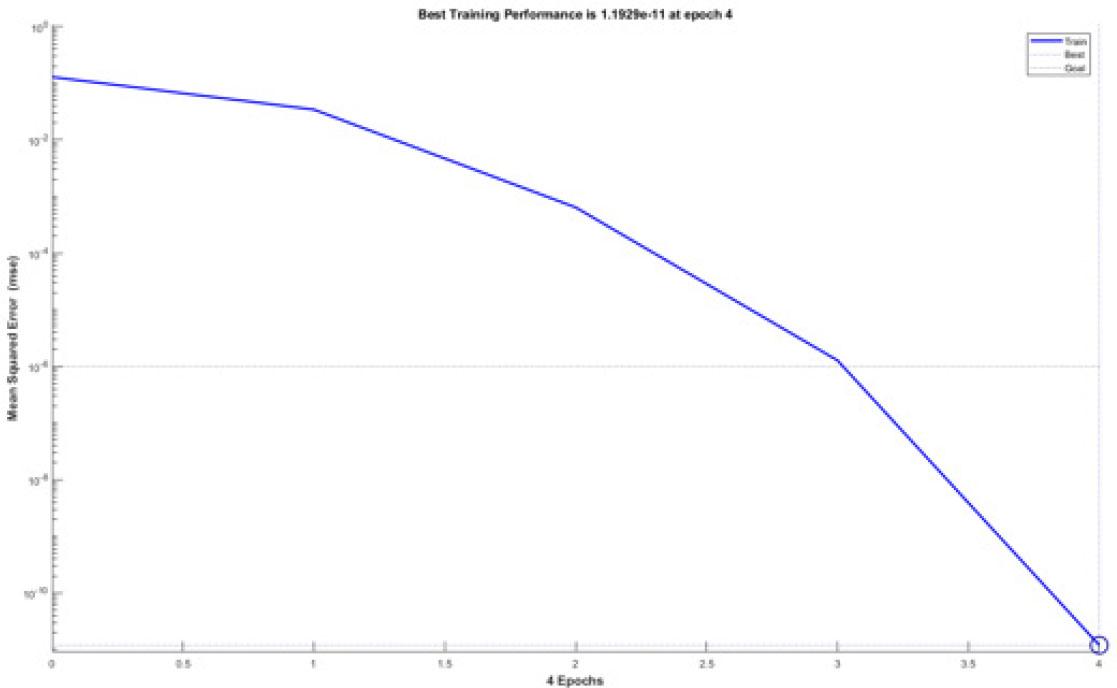
Error curve of BP neural network
In this study, the consumer preference values for the six suit design schemes are compared with the predicted values generated by the BP neural network model. If a significant discrepancy exists between the predicted and actual values, the model is considered invalid; conversely, if the values are closely aligned, the model is deemed valid. A MATLAB program code was developed and executed to evaluate the model’s validity. The predicted values from the model and the corresponding experimental results are summarized in Table 2.
Actual value and predicted value of consumer preference
| Actual value of consumer preference | Normalization of actual value | Predicted value of consumer preference | Normalization of predicted value |
|---|---|---|---|
| 0.49 | 0.50 | 0.15 | 0.00 |
| 0.57 | 1.00 | 0.78 | 1.00 |
| 0.56 | 0.94 | 0.19 | 0.07 |
| 0.43 | 0.13 | 0.74 | 0.93 |
| 0.44 | 0.19 | 0.34 | 0.30 |
| 0.41 | 0.00 | 0.23 | 0.14 |
A matched t-test was conducted to determine whether there was a statistically significant difference between the two sets of normalized data. The two-sided test yielded a p-value of 0.843, indicating that the discrepancy between the consumer preference values predicted by the BP neural network model and the experimentally observed values was not statistically significant. Therefore, the constructed BP neural network structure is considered reliable and can be utilized to develop the subsequent optimization model.
The final output of the suit design optimization model consists of a set of design features which collectively define a specific suit design scheme. To achieve this objective, a systematic framework of suit design elements must be introduced, where each variable corresponds to a qualitative discrete design element. Consequently, a 7-dimensional set of suit design elements is established, as formalized in Equation (1).
Once the specific parameters of these seven-dimensional design elements are determined, a corresponding set of design features can be generated to define a specific suit design scheme. If a particular set of design features maximizes the objective function representing user preference, it can be concluded that this set constitutes the optimal solution for the given objective function.
The number of levels for each variable (design element) is predetermined. For instance, design element Dm has n levels, with each level denoted by Xm1, Xm2, ..., Xmn, meaning that a total of n binary digits are used to encode the values of design variable Dm. Since each design variable must take one and only one level in a given product configuration, a constraint condition is imposed on the seven design variables. In the case of multi-level design variables, each variable must select a unique value within its permissible range, and the corresponding constraint condition is formalized in Equation (2).
This study aims to enhance consumer preference for clothing design and optimize the design scheme using men’s suits as a case study. A higher consumer preference value indicates a more favorable design scheme. A BP neural network model relating suit design features to consumer preference was developed in Section 3. Given a specific set of suit design features, the model is capable of predicting the corresponding consumer preference value for the resulting design scheme. Consumer preference is treated as the objective function and denoted by U, the mathematical formulation for which is presented in Equation (3).
The purpose of constructing the suit design optimization model is to maximize the value of the objective function. Since the objective function is represented by a BP neural network model, which exhibits nonlinear characteristics, traditional linear programming methods are not applicable for finding the optimal solution. Therefore, an appropriate optimization method must be selected to address the problem investigated in this study. The mathematical formulation of the model is presented in Equation (4).
The main ways of traditional genetic algorithm coding include the floating-point coding method, symbolic coding method, and binary coding method. The suit design features in this study involve qualitative 0–1 binary variables. We adopt an encoding mechanism to convert the binary encoding to floating-point encoding first and then convert the floating-point encoding to binary encoding again in the fitness function [32]. The conversion rules are as follows: D1-D7 are seven discrete variables with three-digit encoding, which are converted to continuous variables in the range of [0, 3]. When the value is between [0, 1], the binary code is [1 0 0]; when the value is between [1, 2], the binary code is [0 1 0]; and when the value is between [2, 3], the binary code is [0 0 1].
With the conversion of the above rules, all variables have been converted to continuous type coding, which can be conveniently used for floating-point coding. Each design element occupies a piece of the gene, thus constituting a chromosome with 7 gene segments. Finally, the chromosomes were implanted into the BP neural network, and a fitness calculation function program was written and run in an M function file in MATLAB.
The initial population can be either automatically generated by the built-in function or manually specified using the gaoptimset function. However, due to the high randomness inherent in the automatically generated initial population, its use may hinder subsequent genetic algorithm operations, such as crossover and variation. To address this issue, this study employs 16 suit samples designed based on the orthogonal test as the initial population for the genetic algorithm. The design flow of the integrated BP neural network and genetic algorithm is illustrated in Figure 5, and the corresponding implementation is carried out by executing the code in MATLAB.
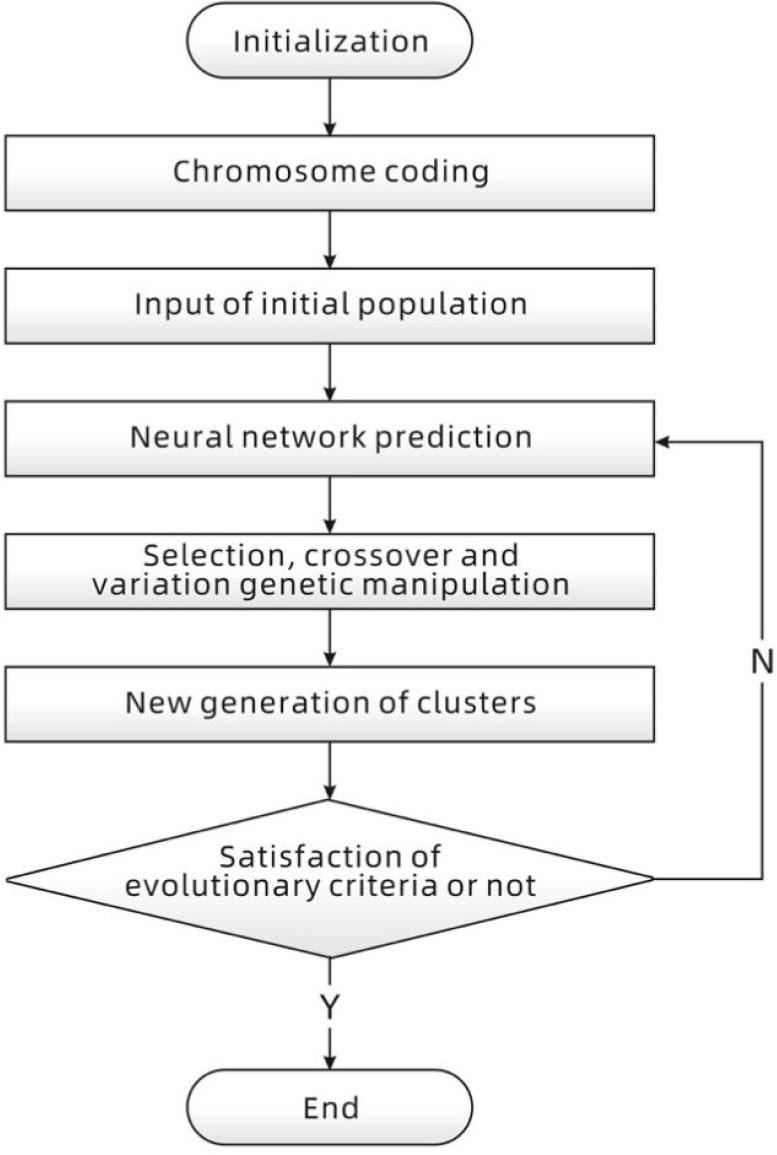
Design flow of integrated algorithm
After multiple iterations of code execution and validation, the result that exhibits a higher frequency of occurrence among the superior optimization outcomes is selected as the optimal decision variable, i.e., X = [100, 100, 100, 001, 001, 001, 100]. The corresponding design features are presented in Table 3.
Optimization scheme of a men’s suit
| Design element | Design feature | Graphical Presentation |
|---|---|---|
| Fabric (A) | Solid color (A1) | |
| Color (B) | Black (B1) | |
| Silhouette (C) | V (C1) | |
| Collar opening (D) | Single row 3 button (D3) | |
| Bottom hem (E) | Big rounded corner (E3) | |
| Collar type (F) | Shawl collar (F3) | |
| Waist pocket (G) | Double-besom pocket (G1) |
Based on the optimal feature combination generated by the model, a specific design scheme can be developed. To apply the optimization results to practical design scenarios, a fashion illustration of a suit was created as shown in Figure 6, and the visual effect of the design and the validity of the model will be verified.

Optimization scheme of a men’s suit
Ninety-seven male participants were invited to conduct a preference survey on suit design, each of whom was required to evaluate 17 images of men’s suits, including 1 optimized scheme and 16 sample schemes. Compared with the sample schemes, the optimized scheme achieved the highest preference score (0.91), indicating that the optimization method for men’s suits received a significantly higher design evaluation.
Men’s clothing began to change from the French Revolution in 1789, shifting from a luxurious aesthetic to one characterized by simplicity and functionality [33]. The 2025–2031 China Men’s Suit Industry Market Analysis and Trend Forecast Report suggests that the design trend of suits integrates natural shoulder lines and a slightly cinched waist, balancing formality and casualness, suitable for various occasions. The optimized V-shaped silhouette aligns with the slightly cinched waist trend, while the shawl collar adds a casual touch to the outfit, making it more comfortable to wear in various scenarios. The double besom pocket design adds a touch of sophistication, and black represents the fashionable color favored by consumers. Research indicates that black is the most preferred color for fashionable outerwear among consumers [34].
The effect of clothing design directly influences consumers’ evaluation and preference for clothing products. This study provides a method to generate higher-quality clothing design schemes, effectively optimizing the design of men’s suits. The clothing design process and algorithm used in this paper can be applied to various types of clothing design, enhancing the market competitiveness of products.
In practical applications, clothing enterprises can utilize this method to comprehensively incorporate consumer preferences during the product design stage, thereby reducing design subjectivity, lowering product development costs, and mitigating market risks. Furthermore, this approach facilitates the transformation of the clothing industry from traditional experience-based design toward data-driven and user-demand-oriented intelligent design.
Future research can integrate the prediction of fashion design trends with the optimization of fashion design, combining big data-driven fashion trend prediction methods with optimization design algorithms to generate more comprehensive design models. Additionally, experimental research can be conducted on physical garments to obtain more multi-dimensional user experiences, further enhancing the efficiency and quality of design optimization.