Puistu ruumilise struktuuri arvutuslik kirjeldamine

Põldveer, Eneli; Laarmann, Diana; Korjus, Henn

doi:10.2478/fsmu-2022-0006

Figures & Tables

20-meetrise raadiusega püsiproovitüki skeem. KU – harilik kuusk (Picea abies (L.) H. Karst.), KS – aru- või sookask (Betula pendula Roth, B. pubescens Ehrh.), HB – harilik haab (Populus tremula L.), JT – teised puuliigid.

Struktuuri mitmekesisuse indeksi SCI keskmised väärtused koos standardhälbega (miinimum- ja maksimumväärtused kuvatud sulgudes) sõltuvalt metsatüübist (kaitsealused, majandatavad ja karjäärimetsad) ja kasvukoha headusest (viljakad ja väheviljakad kasvukohad)_

	Kaitsealused metsad	Majandatavad metsad	Karjäärimetsad
Viljakad	7,42 ± 1,20 (3,16 – 10,22)	4,74 ± 1,44 (1,86 – 10,78)	–
Väheviljakad	3,85 ± 0.87 (1,99 – 5,90)	4,00 ± 1,22 (1,72 – 6,77)	2,64 ± 0,69 (1,36 – 4,15)

Struktuuriindeksite keskmised väärtused koos usaldusvahemikega 95% usaldusnivoo korral vastavalt puistu enamuspuuliigile ja looduslikkuse tasemele_ Erinevad värvid tähistavad statistiliselt olulisi erinevusi (p < 0,05) erineva looduslikkuse tasemega metsade vahel vastavalt Kruskal-Wallise testile_ M¯ \overline M – liigilise segunemise, DM¯ \overline {DM} – surnud puude ruumilise paiknemise, D¯ \overline D – elusate ja surnud puude segunemise, T¯ \overline T – diameetrite diferentseerumise ja W¯ \overline W – puude ruumilise paiknemise indeksid_

	Looduslikkuse tase	M¯ \overline M	DM¯ \overline {DM}	D¯ \overline D	T¯ \overline T	W¯ \overline W
Harilik kuusk	Majandatav mets	0,17 (0,13; 0,21)	0,15 (0,11; 0,19)	0,10 (0,07; 0,12)	0,31 (0,30; 0,33)	0,47 (0,46; 0,48)
	Taastuv mets	0,28 (0,22; 0,34)	0,10 (0,06; 0,15)	0,10 (0,07; 0,13)	0,40 (0,37; 0,43)	0,49 (0,47; 0,50)
	Looduslik mets	0,35 (0,29; 0,41)	0,12 (0,06; 0,18)	0,08 (0,06; 0,11)	0,45 (0,43; 0,48)	0,49 (0,48; 0,51)

Harilik mänd	Majandatav mets	0,43 (0,39; 0,46)	0,13 (0,09; 0,16)	0,08 (0,07; 0,09)	0,36 (0,34; 0,38)	0,48 (0,47; 0,49)
	Taastuv mets	0,44 (0,41; 0,47)	0,12 (0,10; 0,15)	0,11 (0,09; 0,13)	0,41 (0,39; 0,44)	0,49 (0,48; 0,50)
	Looduslik mets	0,44 (0,37; 0,50)	0,18 (0,14; 0,22)	0,15 (0,12; 0,17)	0,44 (0,43; 0,46)	0,49 (0,48; 0,50)

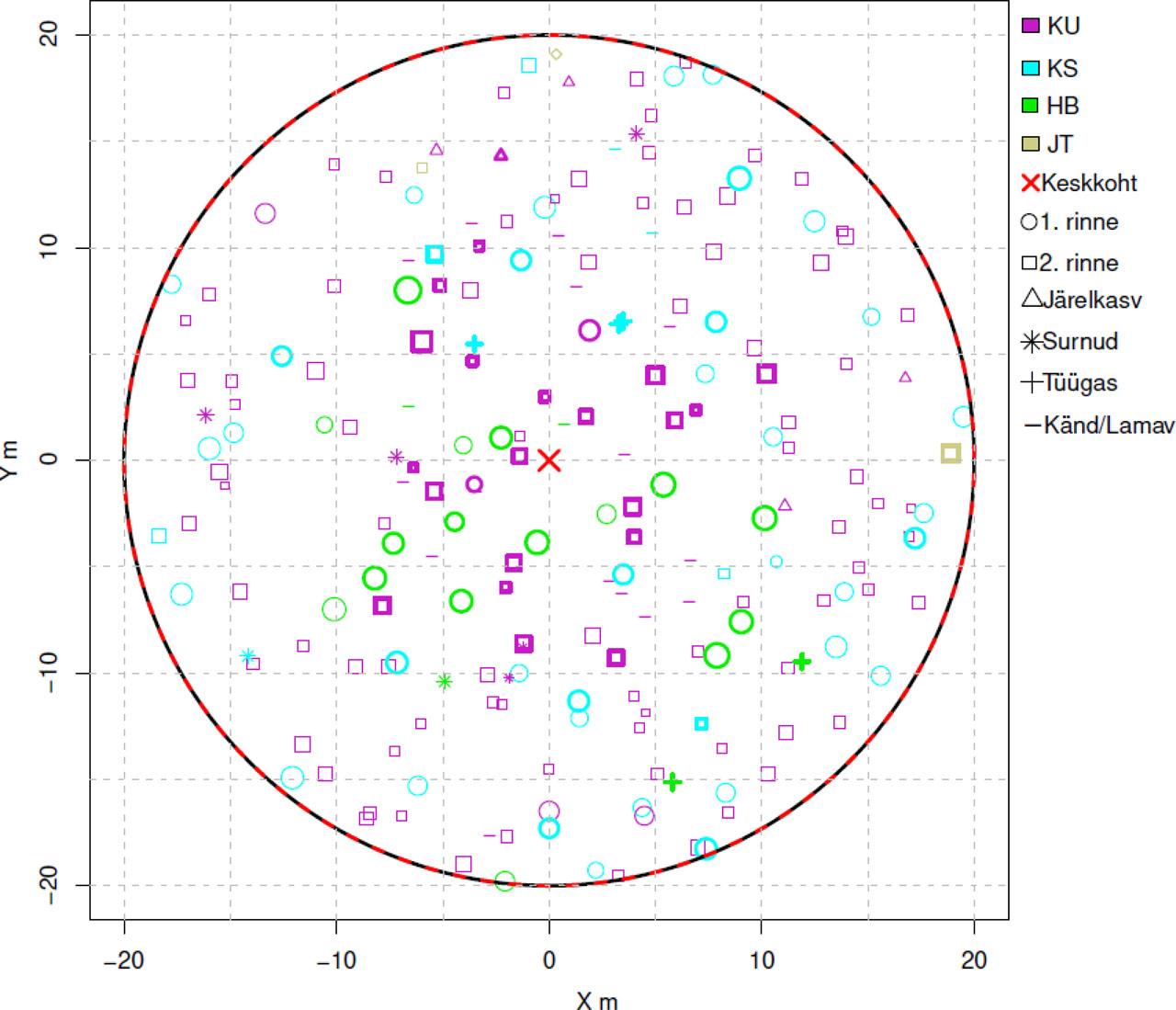
Puistu ruumilist struktuuri kirjeldavad indeksid_ Tase – indeksi esmane arvutamise tase (puu tasemel, puistu tasemel)_ Indeksite arvutamisel proovitüki tasemel tuleb korrigeerida servaefekti_ Detailsema ülevaate saamiseks vaata Põldveer (2022)_

Indeksi nimetus	Tähis	Viide	Tase	Valem
Liigiline segunemine	M_i	Gadow, 1993	puu	Mi=1k∑j=1kvj {M_i} = {1 \over k}\sum\limits_{j = 1}^k {{v_j}}
					M_i ∈ [0,1]
				kus: i – referentspuu; j – referentspuu naaberpuu
				vj={1,kui liik j≠liik i0, vastupidi {V_j} = \left\{ {\matrix{ {1,kui\;liik\;j \ne liik\;i} \cr {0,\;vastupidi} \cr } } \right.

Surnud puude ruumiline paiknemine	DM_i	Laarmann et al., 2009	puu	DMi=1k∑j=1kvj D{M_i} = {1 \over k}\sum\limits_{j = 1}^k {{v_j}}
					DM_i ∈ [0,1]
				kus: i – surnud referentspuu; j – referentspuu naaberpuu
				vj={1, kui naaberpuu j on surnud puu0, vastupidi {v_j} = \left\{ {\matrix{ {1,\;kui\;naaberpuu\;j\;on\;surnud\;puu} \cr {0,\;vastupidi} \cr } } \right.

Elusate ja surnud puude segunemine	D_i	Põldveer et al., 2020	puu	Di=1k∑j=1kvj {D_i} = {1 \over k}\sum\limits_{j = 1}^k {{v_j}}
					D_i ∈ [0,1]
				kus: i – elus referentspuu; j – referentspuu naaberpuu
				vj={1, kui naaberpuu j on surnud puu0, vastupidi {v_j} = \left\{ {\matrix{ {1,\;kui\;naaberpuu\;j\;on\;surnud\;puu} \cr {0,\;vastupidi} \cr } } \right.

Diameetrite diferentseeru mine	T_i	Gadow, 1999	puu	Ti=1−1k∑j=1kmin(di,dj)max(di,dj), {T_i} = 1 - {1 \over k}\sum\nolimits_{j = 1}^k {{{\min \left( {{d_i},{d_j}} \right)} \over {max \left( {{d_i},{d_j}} \right)}}} ,
					T_i ∈ [0,1]
				kus: i – referentspuu; j – referentspuu naaberpuu; d – puu diameeter

Puude ruumiline paiknemine	W_i	Gadow & Hui, 2002	puu	Wi=1k∑j=1kvj {W_i} = {1 \over k}\sum\limits_{j = 1}^k {{v_j}}
					W_i ∈ [0,1]
				kus: i – referentspuu; j – referentspuu naaberpuu; a_j – naaberpuude vaheline nurk, ≤ 180°; α_o – standardnurk (360° / k + 1), 72° kui naaberpuude arv (k) on 4 (Hui & Gadow, 2002)
				vj={1, kui aj < αo0, vastupidi {v_j} = \left\{ {\matrix{ {1,\;kui\;{a_j}\; < \;{\alpha _{\rm{o}}}} \cr {0,\;vastupidi} \cr } } \right.

Puistu struktuuri mitmekesisus	SCI	Zenner, 1998	puistu	SCI = SCI^/A_T*,	kus: A_T – mittekattuvate kolmnurkade pindalade summa, mis arvutatakse puu x- ja y-koordinaatide järgi kasutades Delaunay triangulatsiooni protseduuri

				kusjuures SCI=∑i=1N12\|a×b\| {\rm{SCI}}^ = \sum\limits_{i = 1}^N {{1 \over 2}\left\| {a \times b} \right\|}	N – kolmnurkade arv proovitükil, \|a × b\| – vektorite AB: koordinaadid a = (x_b − x_a, y_b − y_a, z_b − z_a) ja AC: koordinaadid b = (x_c − x_a, y_c − y_a, z_c − z_a) absoluutväärtused.

Puistu ruumilise struktuuri arvutuslik kirjeldamine

Figures & Tables

Joonis 1

Struktuuri mitmekesisuse indeksi SCI keskmised väärtused koos standardhälbega (miinimum- ja maksimumväärtused kuvatud sulgudes) sõltuvalt metsatüübist (kaitsealused, majandatavad ja karjäärimetsad) ja kasvukoha headusest (viljakad ja väheviljakad kasvukohad)_

Puistu ruumilist struktuuri kirjeldavad indeksid_ Tase – indeksi esmane arvutamise tase (puu tasemel, puistu tasemel)_ Indeksite arvutamisel proovitüki tasemel tuleb korrigeerida servaefekti_ Detailsema ülevaate saamiseks vaata Põldveer (2022)_

Paradigm

My account