Socio-ecological systems and the distributional effect of collective conditionality constraints in rural policies: A case study in Emilia-Romagna Cover

Socio-ecological systems and the distributional effect of collective conditionality constraints in rural policies: A case study in Emilia-Romagna

International Journal of the Commons

Volume 12 (2018): Issue 1

By: Matteo Zavalloni , Meri Raggi and Davide Viaggi

Open Access

|Apr 2018

Figures & Tables

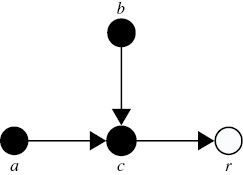
figures/ijc2018-2018014_fig_001.jpg — Example of a network in which a, b, and c represent farms, and r represents the reservoir.

Table 1:

Distribution of water quotas per farm.

No. of quota	No. of farms
1	6
2	9
3	2
4	7
5	0
6	0
7	0
8	2

Table 2:

Cost of pipe network (€/m) according to the amount of water passing through the pipes.

w_ij	€/m
0<w_ij≤4000	7.6
4000<w_ij≤13,000	16.2
13,000<w_ij≤25,000	52
25,000<w_ij	68

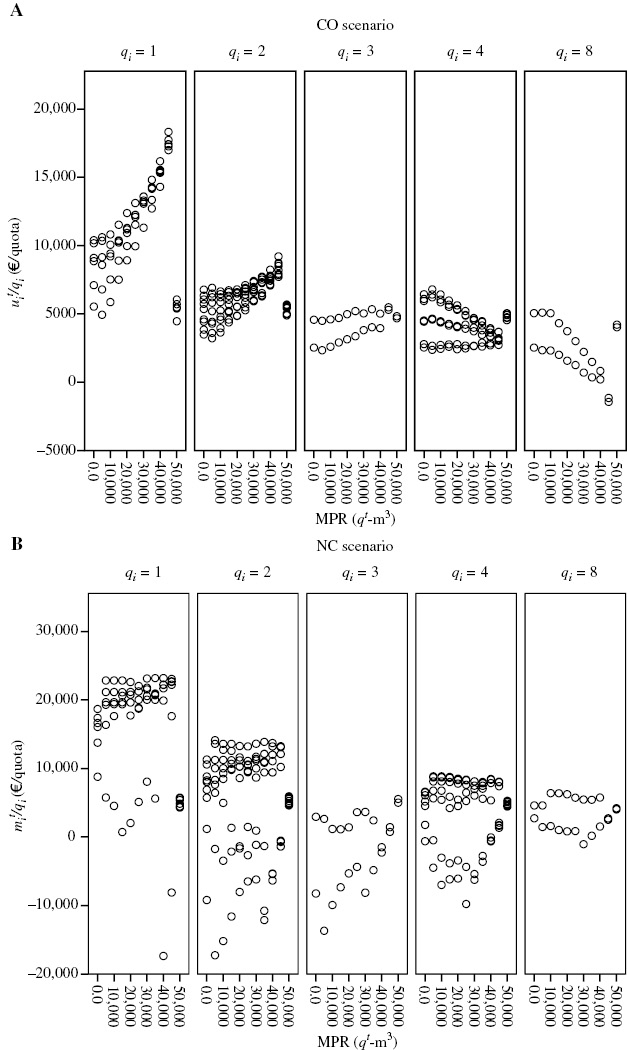
figures/ijc2018-2018014_fig_002.jpg — Allocation of the grand-coalition costs per quota in the CO scenario upper graph – A) and in the NC scenario bottom graph -B) under different MPR levels.

figures/ijc2018-2018014_eq_032.jpg — Allocation of the grand-coalition costs per quota in the CO scenario upper graph – A) and in the NC scenario bottom graph -B) under different MPR levels.

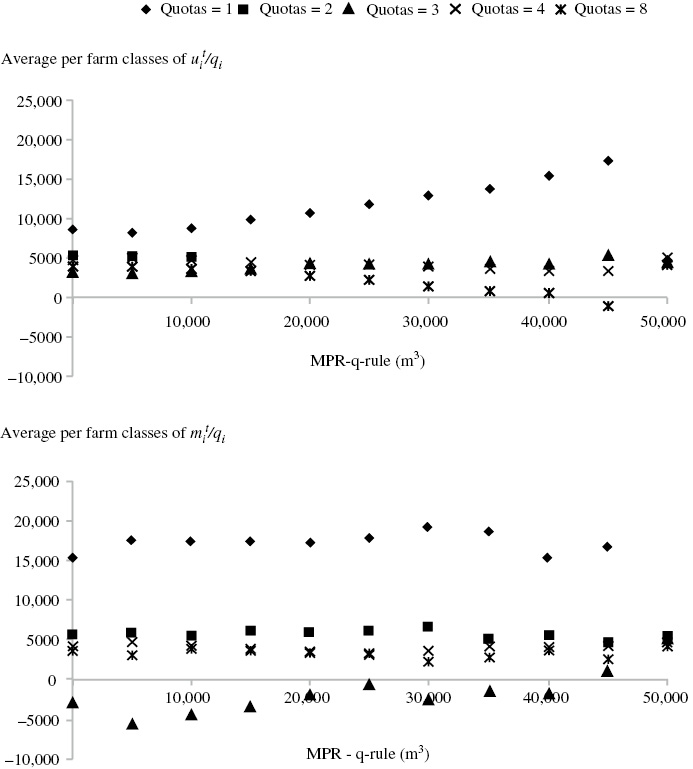
figures/ijc2018-2018014_fig_003.jpg — Average SV in the CO scenario (upper graph) and in the NC scenario (bottom graph) per classes of farms.

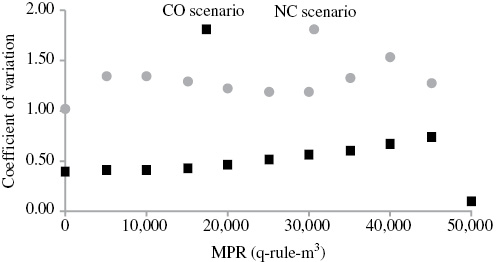
figures/ijc2018-2018014_fig_004.jpg — Coefficient of variation (CV) of average SV in the CO scenario (squares) and in the NC scenario (circles).

Table 3:

List and explanation of variables used in the regression model.

Variable	Explanation
q_i	The amount of water requested by each farm
Distance	The distance of each farm from the reservoir
\|D_i\|	The cardinality of D_i
w_ij	The amount of water passing through each farm
Power	The power of each player

Table 4:

Regression analysis of the cost allocation in the CO scenario.

B	Std. error	Beta
(Constant)	6079.191	1005.981		6.043	0.000
q_i	3566.437	316.49	1.113	11.269	0.000
Distance (km)	0.789	0.19	0.24	4.149	0.000
\|D_i\|	456.278	135.765	0.323	3.361	0.001
w_ij	−0.344	0.065	−0.636	−5.272	0.000
Power	−107436.721	17284.063	−0.498	−6.216	0.000

The dependent variable is figures/ijc2018-2018014_eq_025.jpg .

Table 5:

Regression analysis of the cost allocation in the NC scenario.

B	Std. error	Beta
(Constant)	12640.162	1984.766		6.369	0.000
q_i	4035.225	624.423	0.446	6.462	0.000
Distance (km)	1.857	0.375	0.200	4.953	0.000
\|D_i\|	−2160.643	267.86	−0.541	−8.066	0.000
w_ij	−0.321	0.129	−0.210	−2.497	0.013
power	−60843.952	34100.853	−0.100	−1.784	0.075

The dependent variable is 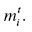figures/ijc2018-2018014_eq_026.jpg

Table 6:

Adjacency matrix representing the weighted directed relations between each node (distance in km).

	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28
0	0	0	0	0	0	0	0	0	0	0	0	0	279	0	0	0	0	0	0	0	0	0	0	0	0	173	750	0	0
1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
2	0	0	0	0	0	0	0	0	0	93	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
3	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	152	0	0	0	0	0	0
4	0	0	0	0	0	957	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
5	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	154	0	0	0	0	0	0	0	0	0
6	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1083	0	0	0	0	0	0	0
7	0	0	0	0	0	0	0	0	323	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
8	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
9	0	0	0	0	0	0	0	0	0	0	189	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
10	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
11	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
12	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1017	0	0	0	0	0	0	0	0
13	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
14	0	0	0	0	0	0	0	0	0	0	0	0	0	270	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
15	0	0	0	0	0	0	340	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
16	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	380	0	0	0	0	0	0	0	0	0	0
17	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	305	0	0	0	0
18	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
19	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	484	0	0	0	0	0	0	0	0	0	0	0
20	0	0	0	844	0	0	0	0	0	0	0	0.1	0	0	0	0	410	0	0	0	0	0	0	0	0	0	0	0	0
21	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	927	0
22	0	0	0	0	755	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
23	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
24	0	0	281	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
25	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
26	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	295	0	0	0	0	0	0	0	0	0	0	0	0	0
27	0	0	0	0	0	0	0	0	0	0	0	0	0	0	804	0	0	0	0	0	0	0	0	0	0	0	0	0	1493
28	0	369	0	0	0	0	0	358	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	17	0	0	0	0	0

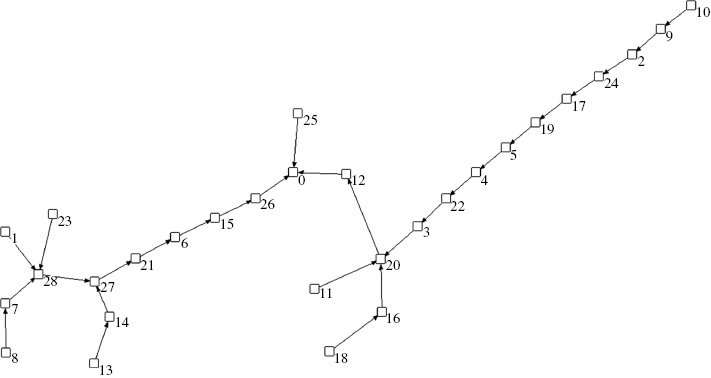
figures/ijc2018-2018014_fig_005.jpg — Graphical representation of the network used in the paper. The network does not account for the actual position in the landscape.

DOI: https://doi.org/10.18352/ijc.833 | Journal eISSN: 1875-0281

Journal RSS Feed

Language: English

Published on: Apr 23, 2018

Published by: Uopen Journals

In partnership with: Paradigm Publishing Services

Publication frequency: 1 issue per year

Keywords:

socio-ecological system,

minimum participation rules,

collective action,

agricultural policies

© 2018 Matteo Zavalloni, Meri Raggi, Davide Viaggi, published by Uopen Journals
This work is licensed under the Creative Commons Attribution 4.0 License.

Previous article Volume 12 (2018): Issue 1 Next article