Groins and submerged breakwaters – new modeling and empirical experience Cover

.blurhash-client-img { display: none !important; }

Groins and submerged breakwaters – new modeling and empirical experience

Oceanological and Hydrobiological Studies

Volume 45 (2016): Issue 1 (March 2016)

By: Rafał Ostrowski, Zbigniew Pruszak, Jan Schönhofer and Marek Szmytkiewicz

Open Access

|Mar 2016

Figures & Tables

Location of the Hel Peninsula in the Baltic Sea

Figure 2

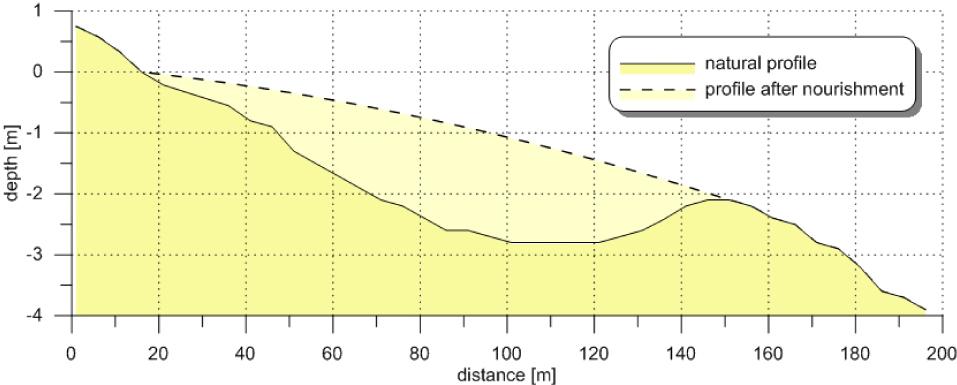
The nearshore part of the cross-shore profile at the Hel Peninsula

Calculated depth-averaged flow velocities for the natural nearshore zone (without groins) in moderate storm conditions (Hs=1 m, Tp=4 s, α=45°)

Calculated depth-averaged flow velocities for full length groins in moderate storm conditions (Hs=1 m, Tp=4 s, α=45°)

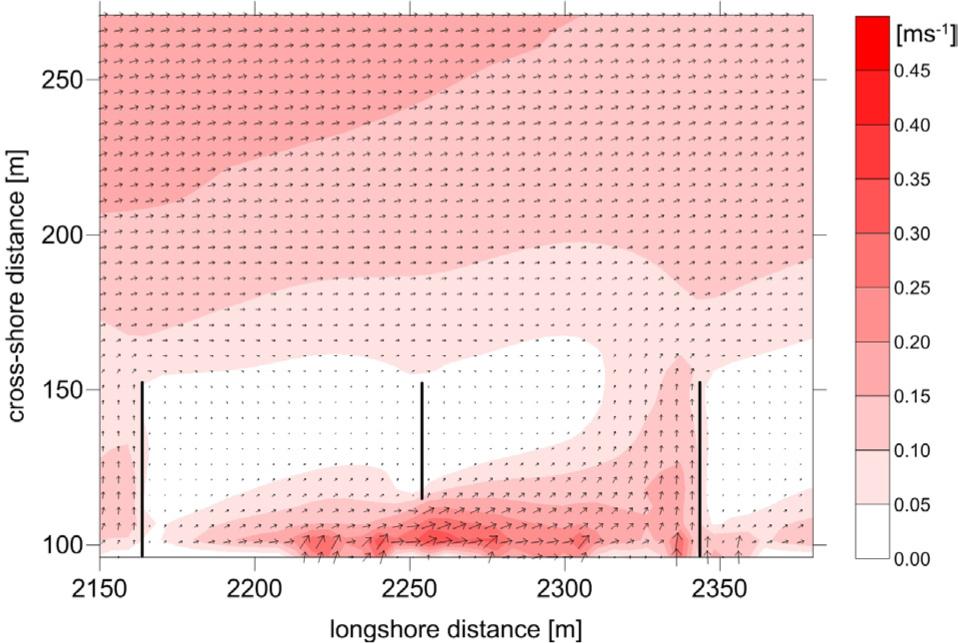
Calculated depth-averaged flow velocities for a groin separated from the shoreline in moderate storm conditions (Hs=1 m, Tp=4 s, α=45°)

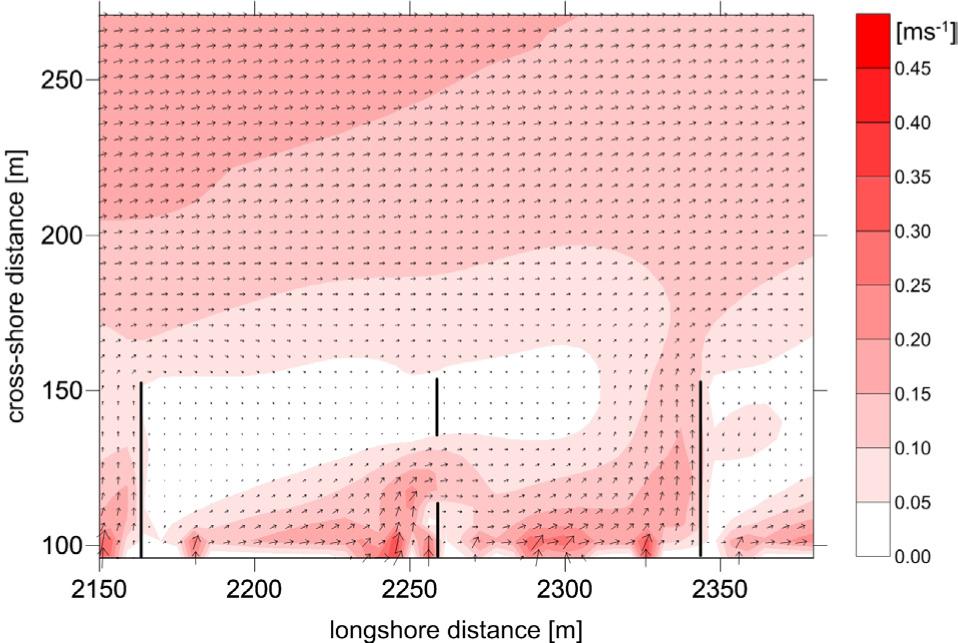
Calculated depth-averaged flow velocities for a groin with a breach about its central part in moderate storm conditions (Hs=1 m, Tp=4 s, α=45°)

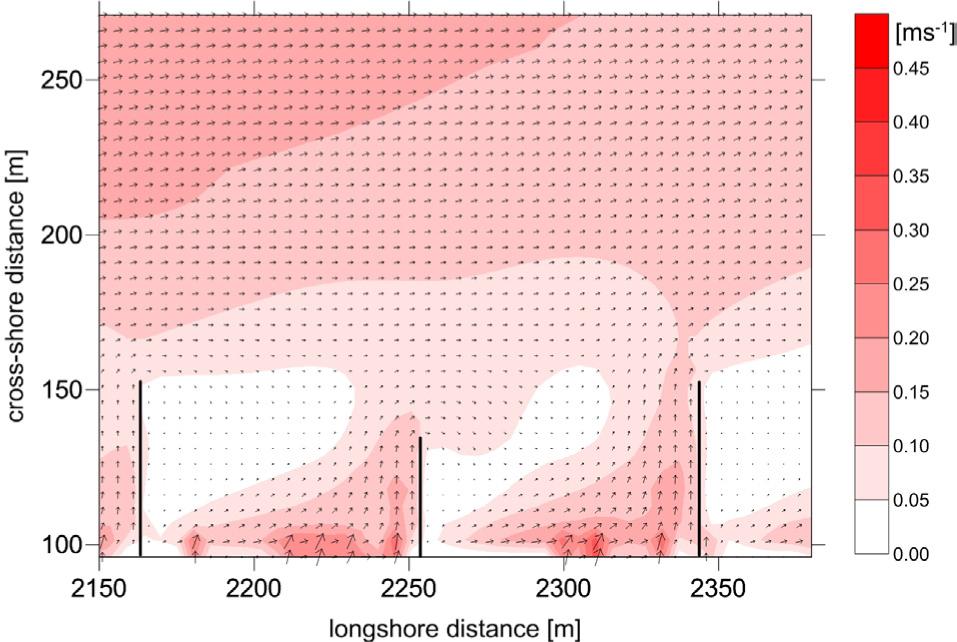
Calculated depth-averaged flow velocities for a groin with missing piles at its end in moderate storm conditions (Hs=1 m, Tp=4 s, α=45°)

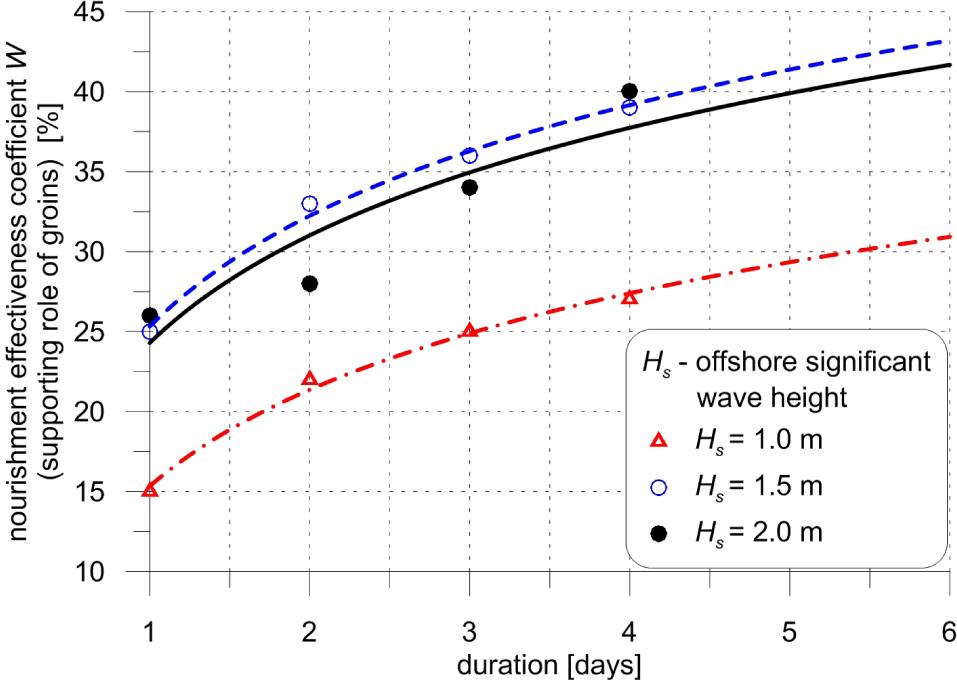
Coefficient W, representing the supporting role of groins in artificial shore nourishment, as a function of time for various offshore wave heights

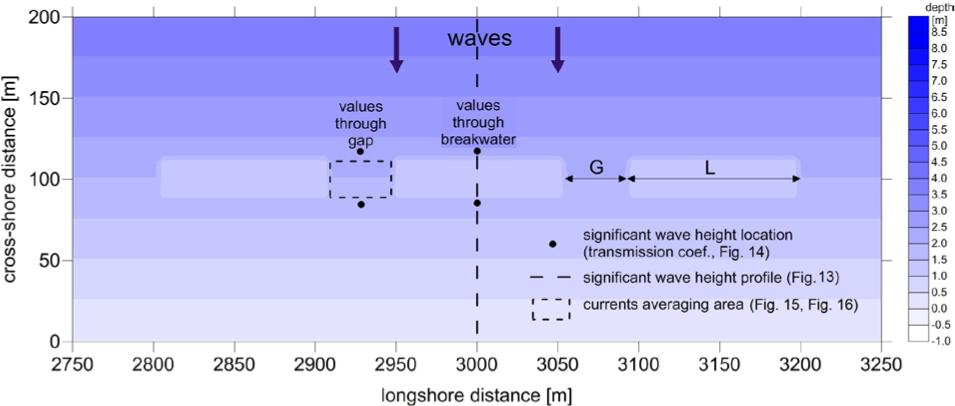
Layout of submerged breakwaters in the nearshore zone (L – breakwater segment length, G – gap length)

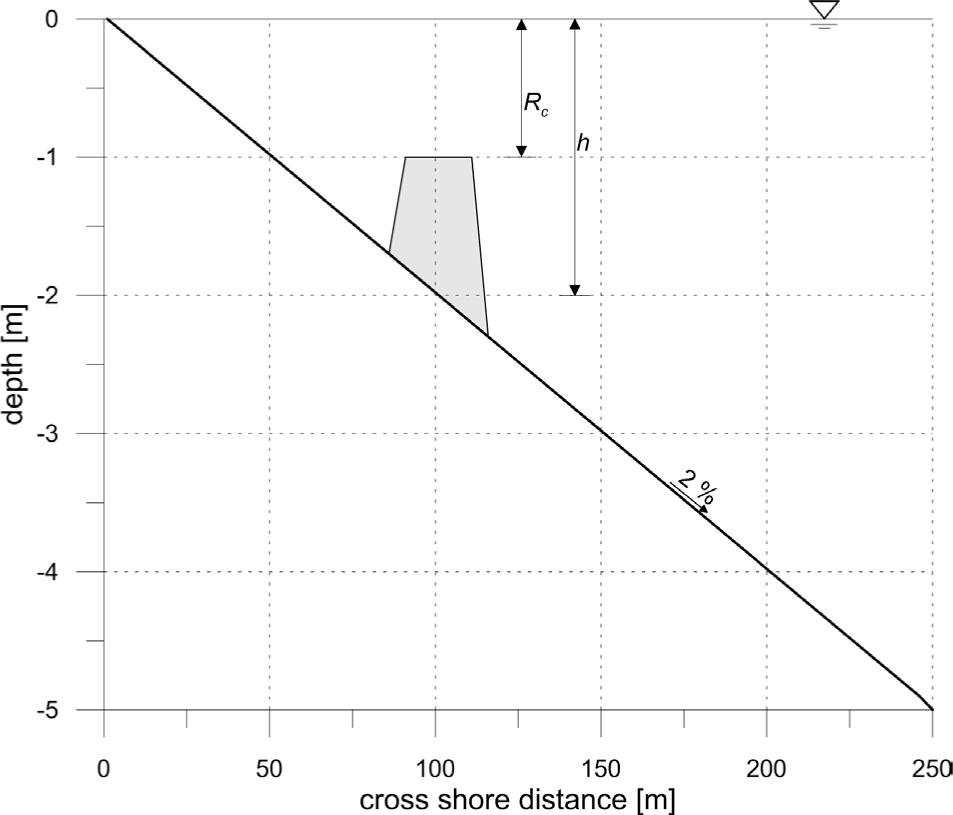
Cross-section of nearshore sea bottom with a submerged breakwater (Rc – water depth at a breakwater crest).

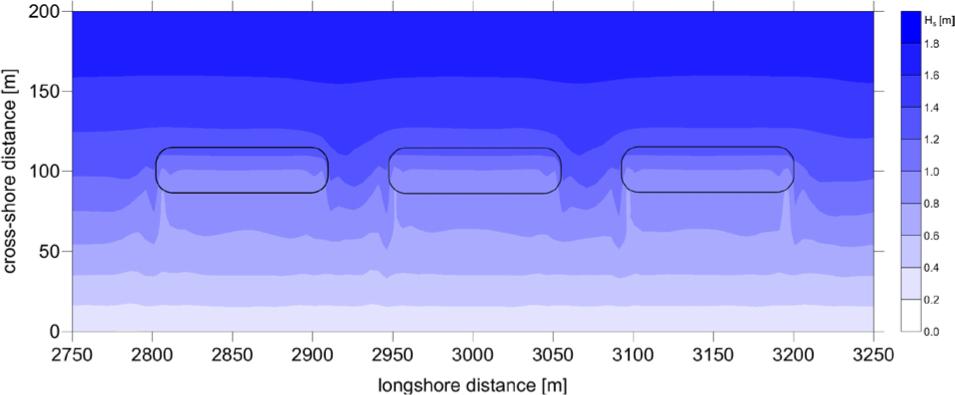
Calculated significant wave heights near submerged breakwaters for Rc/h=0.2 and L/G=2.63 (Hs=2 m, Tp=5.5 s, α=90°)

Calculated flow velocities near submerged breakwaters for Rc/h=0.2 and L/G=2.63 (Hs=2 m, Tp=5.5 s, α=90°)

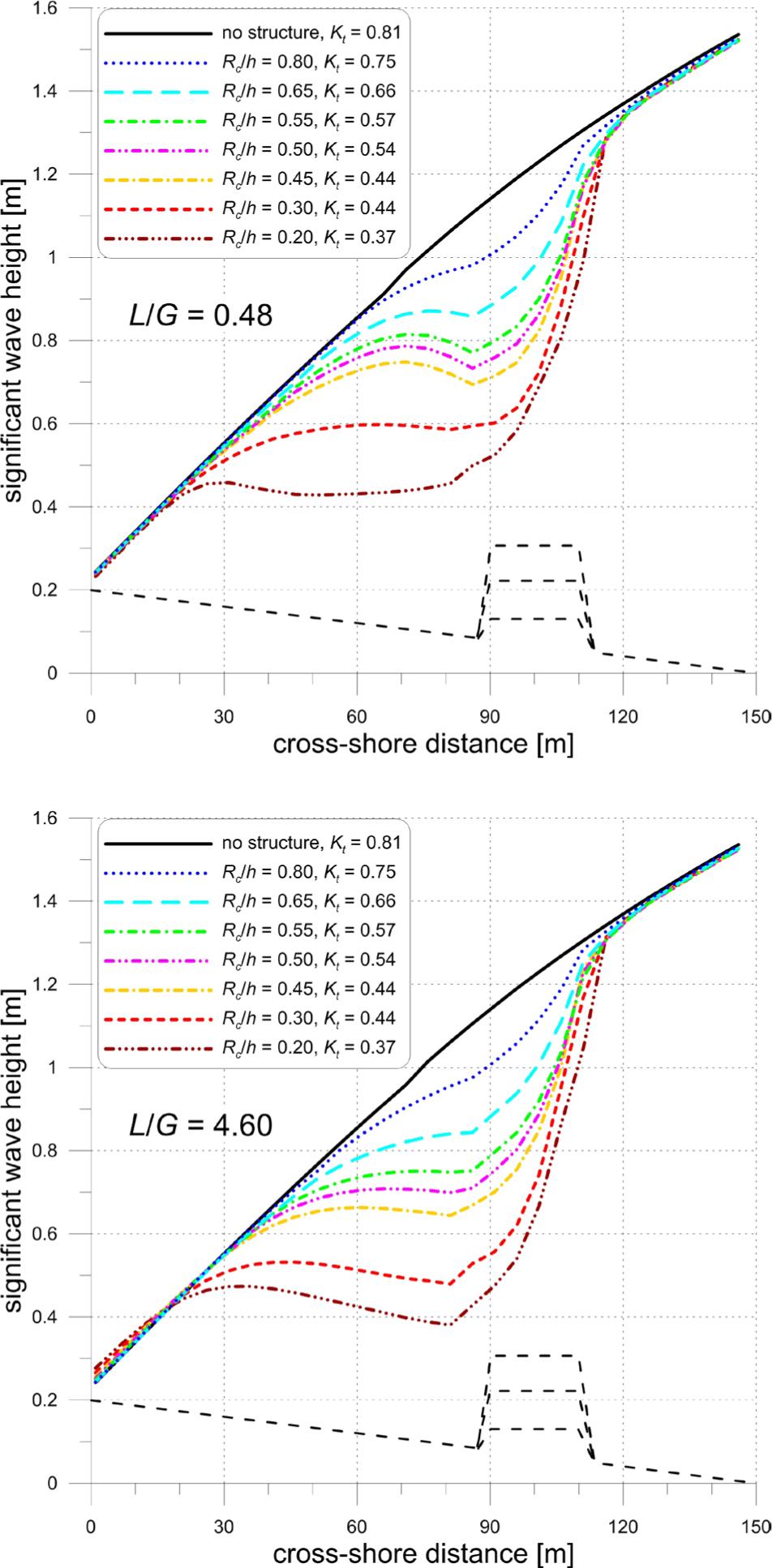
Calculated wave heights at different distances from the shoreline for L/G=0.48 (up) and L/G=4.6 (down) as curves corresponding to various ratios Rc/h resulting in various transmission coefficients Kt (bottom dashed lines indicate location of a breakwater and symbolize variability of its height); Hs=2 m, Tp=5.5 s, α=90°

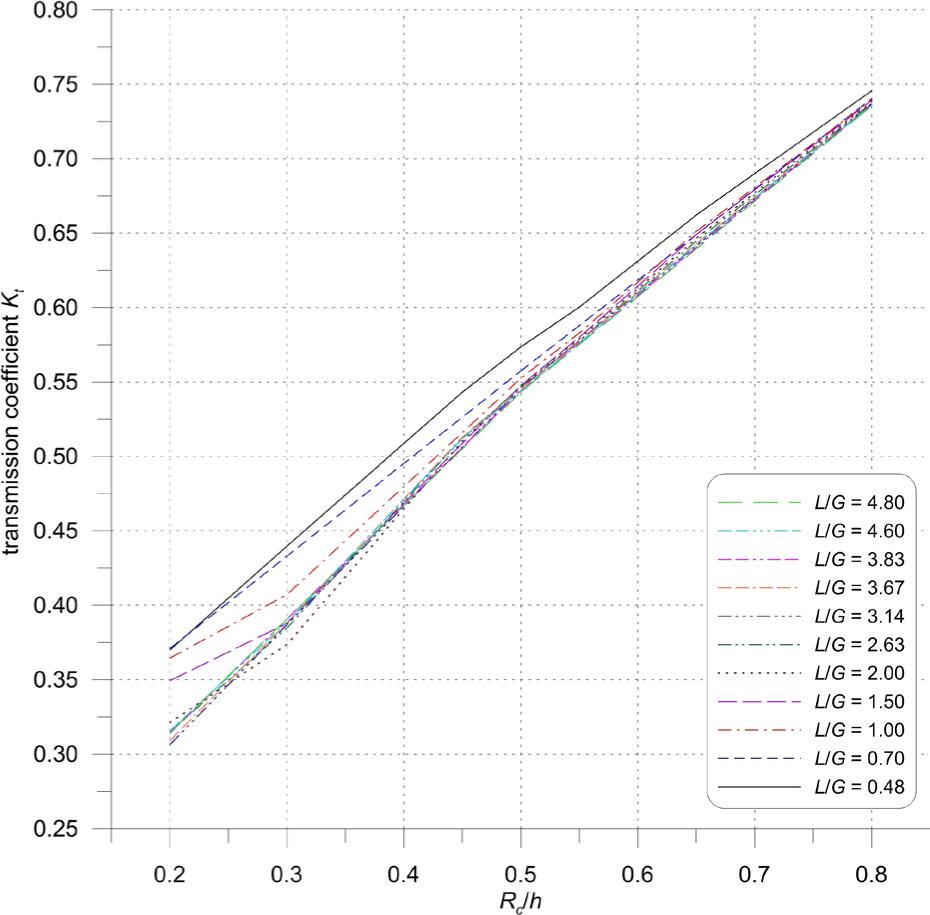
Calculated transmission coefficients Kt as functions of Rc/h for various L/G ratios (Hs=2 m, Tp=5.5 s, α=90°)

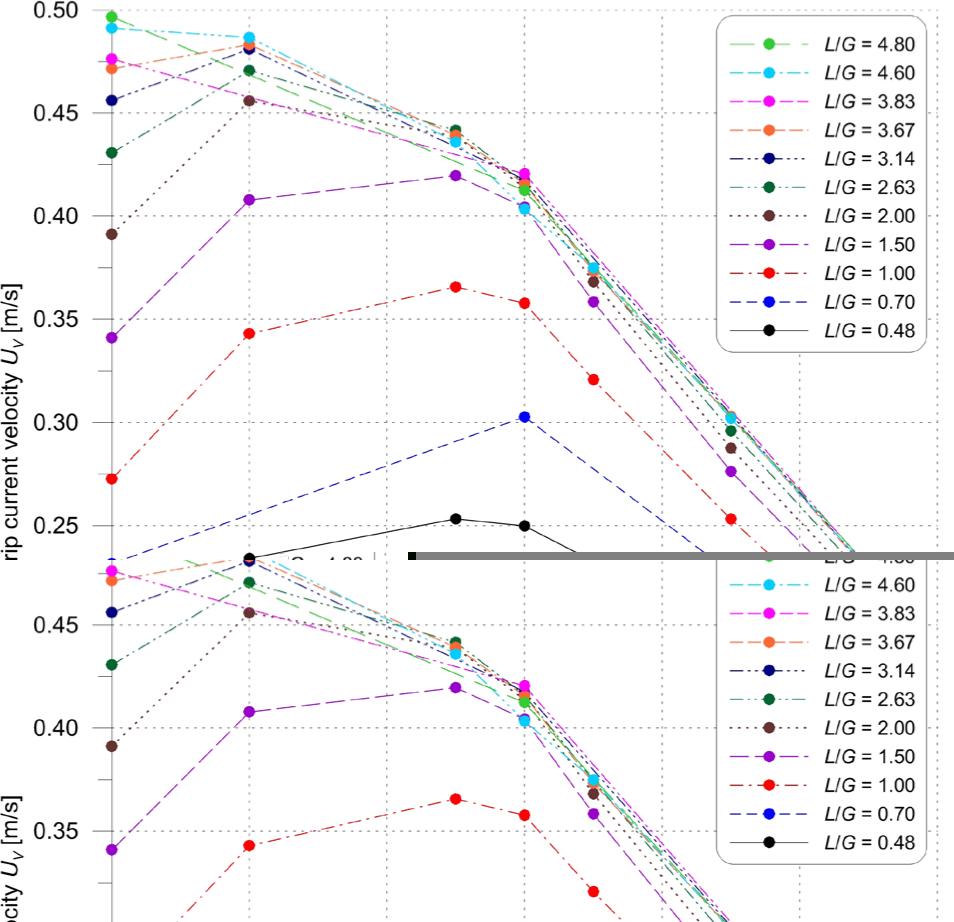
Calculated rip current velocities as functions of Rc/h for various L/G ratios (Hs=2 m, Tp=5.5s, α=90°)

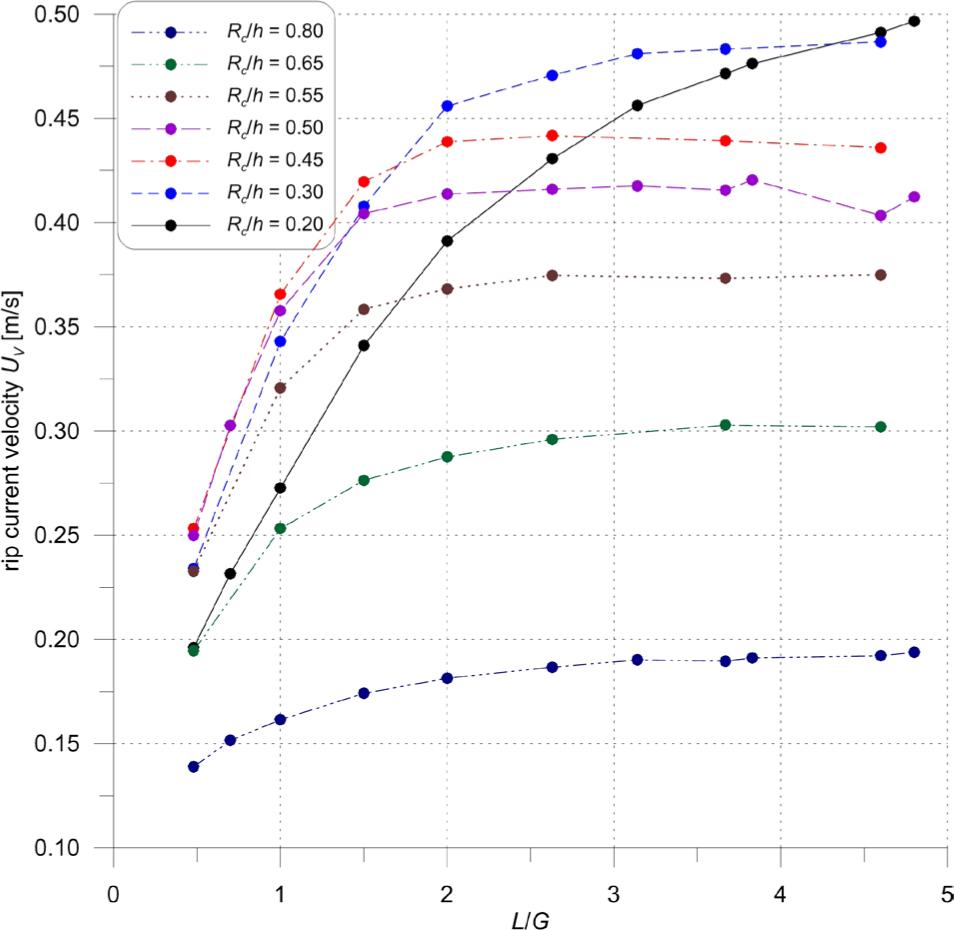
Calculated rip current velocities as functions of L/G for various Rc/h ratios (Hs=2m, Tp=5.5s, α=90°)

Calculated coefficients A, B and C as functions of Rc/h

Coefficients (a and b) and goodness (R2) of linear approximation of the transmission coefficient Kt using the Rc/h ratio for various L/G values and for general approximation

L/G	0.48	0.70	1.00	1.50	2.00	2.63	3.14	3.67	3.83	4.60	4.80	General
A	0.627	0.616	0.644	0.675	0.717	0.712	0.717	0.715	0.704	0.706	0.702	0.686
B	0.253	0.248	0.227	0.205	0.178	0.180	0.171	0.178	0.180	0.183	0.180	0.198
R2	0.997	1.000	0.997	0.995	0.994	0.995	0.996	0.995	0.997	0.996	0.998	0.987

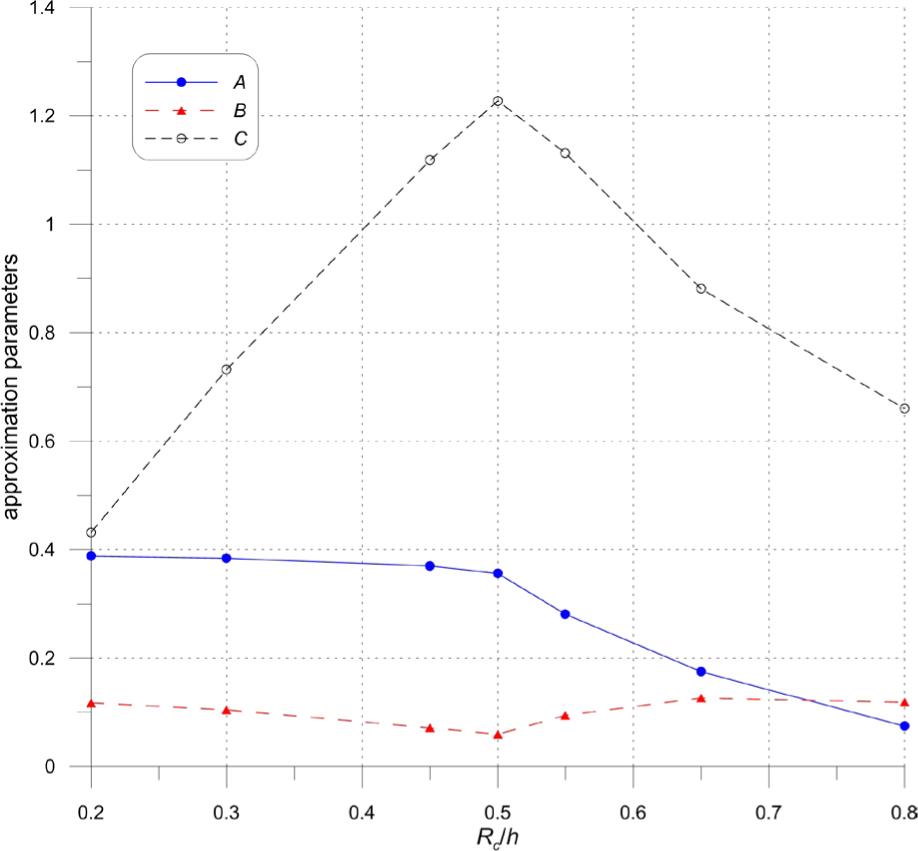
Coefficients (A, B and C) and goodness (R2) of approximation (Eq_ 3) of rip current velocity UV using the L/G ratio for various Rc/h quantities

Rc/h	0.20	0.30	0.45	0.50	0.55	0.65	0.80
A	0.388	0.384	0.370	0.356	0.281	0.175	0.074
B	0.117	0.104	0.071	0.059	0.094	0.126	0.118
C	0.432	0.732	1.118	1.228	1.131	0.881	0.660
R2	1.000	0.999	0.997	0.992	0.999	0.996	0.996

DOI: https://doi.org/10.1515/ohs-2016-0003 | Journal eISSN: 1897-3191 | Journal ISSN: 1730-413X

Journal RSS Feed

Language: English

Page range: 20 - 34

Submitted on: Apr 30, 2015

Accepted on: Jul 22, 2015

Published on: Mar 10, 2016

Published by: University of Gdańsk

In partnership with: Paradigm Publishing Services

Publication frequency: 4 issues per year

Keywords:

submerged breakwaters,

interaction with artificial shore nourishment,

Related subjects:

Chemistry, other,

Geosciences, other,

Life sciences, other

© 2016 Rafał Ostrowski, Zbigniew Pruszak, Jan Schönhofer, Marek Szmytkiewicz, published by University of Gdańsk
This work is licensed under the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 License.

Previous article Volume 45 (2016): Issue 1 (March 2016)Next article