Table 1
Prior distributions of the marker effects and indicator variables.a
| Hierarchical level | |||
|---|---|---|---|
| 1st | 2nd | 3rd | |
| BL | |||
| EBL | |||
| wBSR | |||
| BayesB | |||
| BayesC | |||
| SSVS | |||
| MIX | |||
[i] aPrior distributions of the marker effects have three-level hierarchical structures for BL and EBL, and two-level for the other methods.
BL, Bayesian lasso; EBL, extended Bayesian lasso; wBSR, weighted Bayesian shrinkage regression; SSVS, stochastic search variable selection; MIX, Bayesian mixture regression; N, normal distribution; Inv-G, inverse-gamma distribution; G, gamma distribution; Bernoulli, Bernoulli distribution; χ-2, scaled inverse-chi-square distribution.
Table 2
Hyperparameters required by vigor.
| Regression | Hyperparametersa | Less influential hyperparameters (default values) | Influential hyperparameters determined by hyperpara |
|---|---|---|---|
| BL | φ, ω | φ (1.0) | ω |
| EBL | φ, ω, ψ, θ | φ (0.1), ω (0.1), ψ (1.0) | θ |
| wBSR | v, S2, κ | v (5.0) | S2 |
| BayesB | v, S2, κ | v (5.0) | S2 |
| BayesC | v, S2, κ | v (5.0) | S2 |
| SSVS | c, v, S2, κ | v (5.0) | c, S2 |
| MIX | c, v, S2, κ | v (5.0) | c, S2 |
[i] aFor each regression model, the hyperparameters in this table correspond to those listed in Table 1. Among these hyperparameters, κ of wBSR, BayesB, BayesC, SSVS, and MIX is determined by the user. The other hyperparameters are set as default or can be determined by the function hyperpara.
BL, Bayesian lasso; EBL, extended Bayesian lasso; wBSR, weighted Bayesian shrinkage regression; SSVS, stochastic search variable selection; MIX, Bayesian mixture regression.

Figure 1
Overview of analysis by VIGoR. VIGoR consists of two programs/functions, vigor and hyperpara. Vigor conducts genome-wide regression analysis and has three main functions; Model fitting, Model fitting after hyperparameter tuning, and Cross-validation. The former two functions output the estimates of the marker and covariate effects, and the fitted values. The last function outputs the predicted values obtained by cross-validation. Vigor requires three kinds of input information, phenotypic values (response variable), marker genotypes (predictor variable), and hyperparameter values. Hyperparameter values can be determined by the user or by using hyperpara. Hyperpara calculates the values of hyperparameters that influence on inference, based on the assumptions of the genetic architecture and values of hyperparameters that influence less.
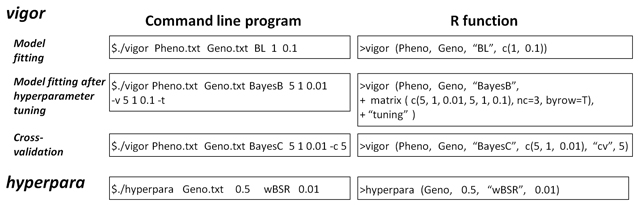
Figure 2
Examples of the usage of vigor and hyperpara. “sample.pheno.txt” and “PhenoHeight” are the example file and object that contain the phenotypic values (response variables), and “sample.geno.txt” and “Geno” are the example file and object that contain the marker genotypes (predictor variables). These files and objects are included in the com¬mand line program (CLP) and R packages, respectively. The regression methods are specified by their abbreviations (e.g., BL, BayesB, and wBSR). The argument(s) immediately after the regression methods are the hyperparameter values. Hyperparameters should be ordered as in the second column of Table 2. In the example of Model fitting, 1 and 0.1 are the values of φ and ω of Bayesian lasso, respectively. In the example of Model fitting after hyperparameter tuning, two hyperparameter value sets, [v = 5, S2 = 1, κ=0.01] and [v = 5, S2 = 1, κ = 0.1], are provided using the -v option (CLP) and as a matrix (R function). The better set is chosen using cross-validation (CV), and model fitting is performed automatically with the chosen set. The -t option (CLP) and the argument “tuning” (R function) indicate this procedure. In the example of Cross-validation, a five-fold CV is performed. The -c option (CLP) and “cv” (R function) indicate CV, and the argument immediately after this option/argument (here 5) is the fold number. In the example of hyperpara, the second (0.5) and fourth (0.01) arguments are the values of Mvar and κ, respectively (see the main text for the explanations of Mvar and κ).
