Figure 1
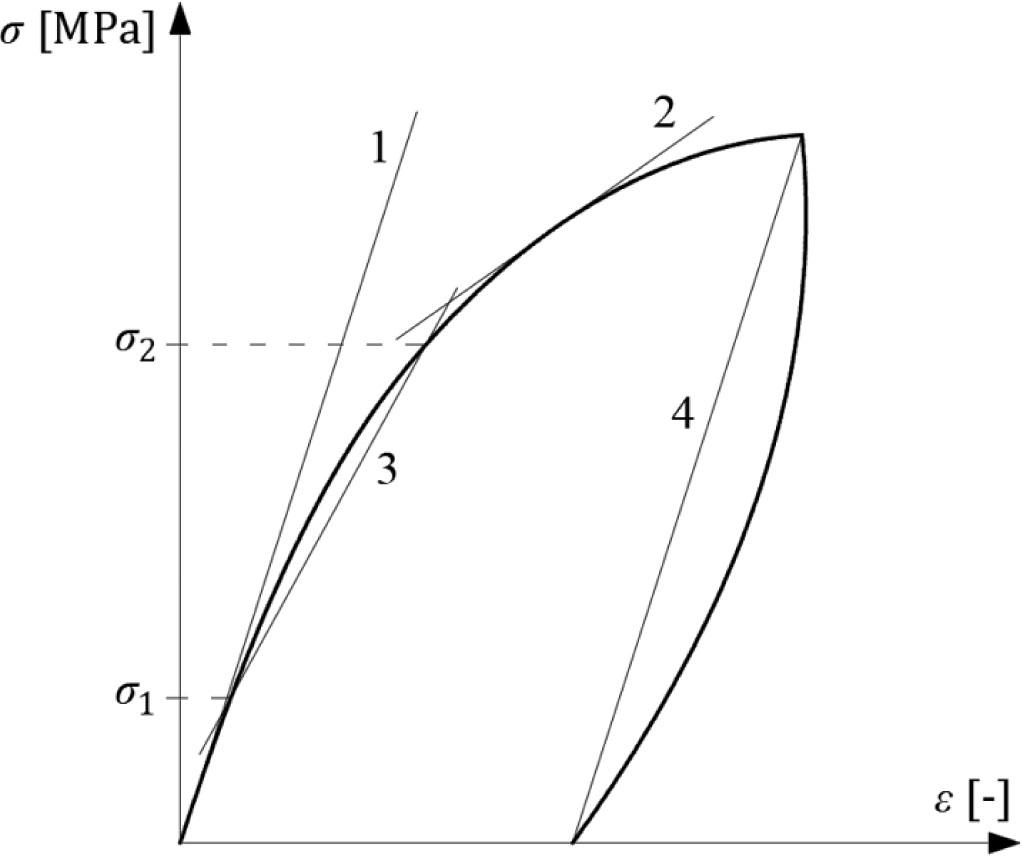
Figure 2
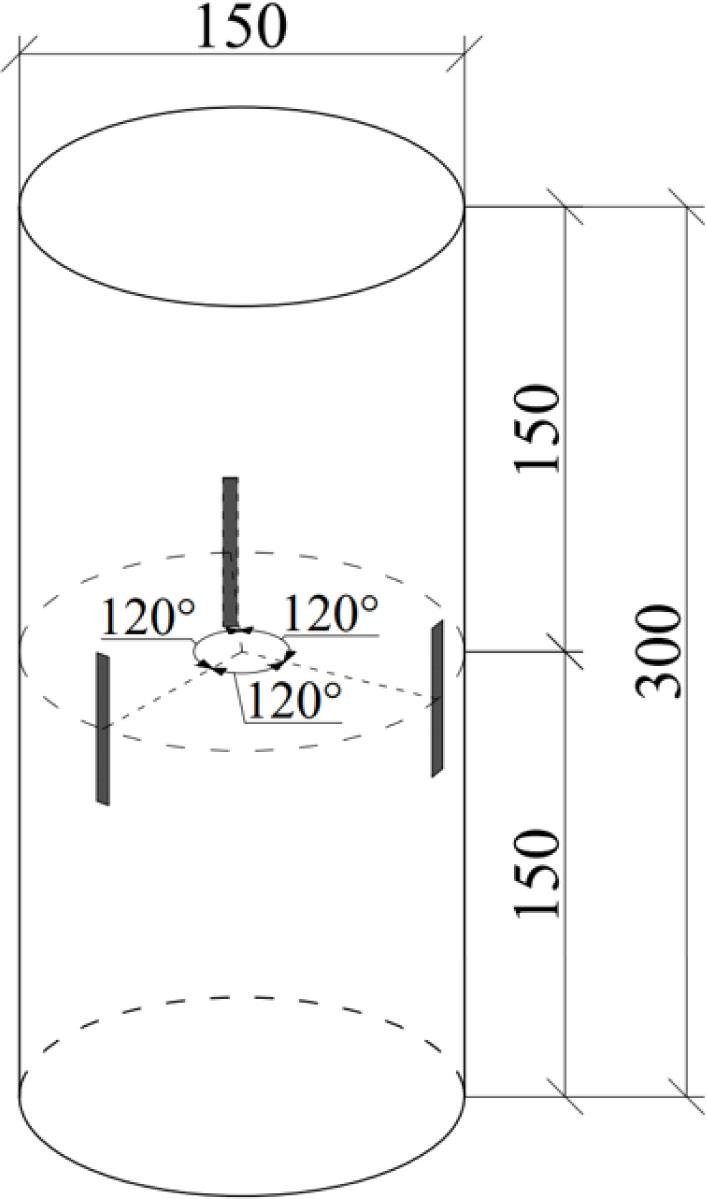
Figure 3
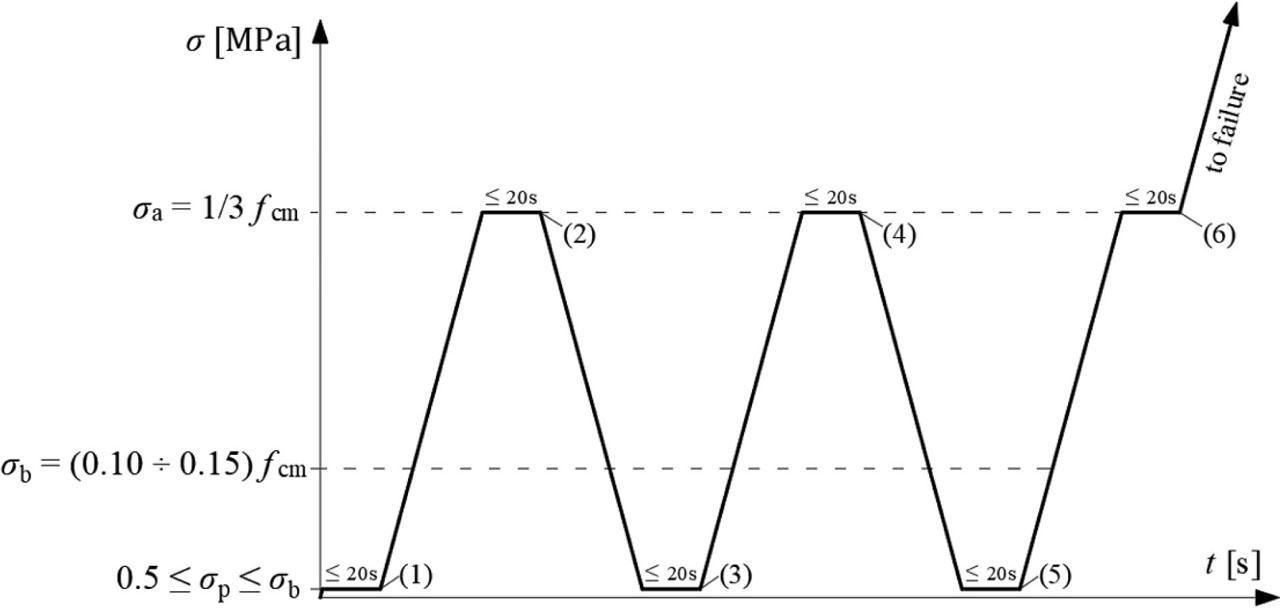
Figure 4
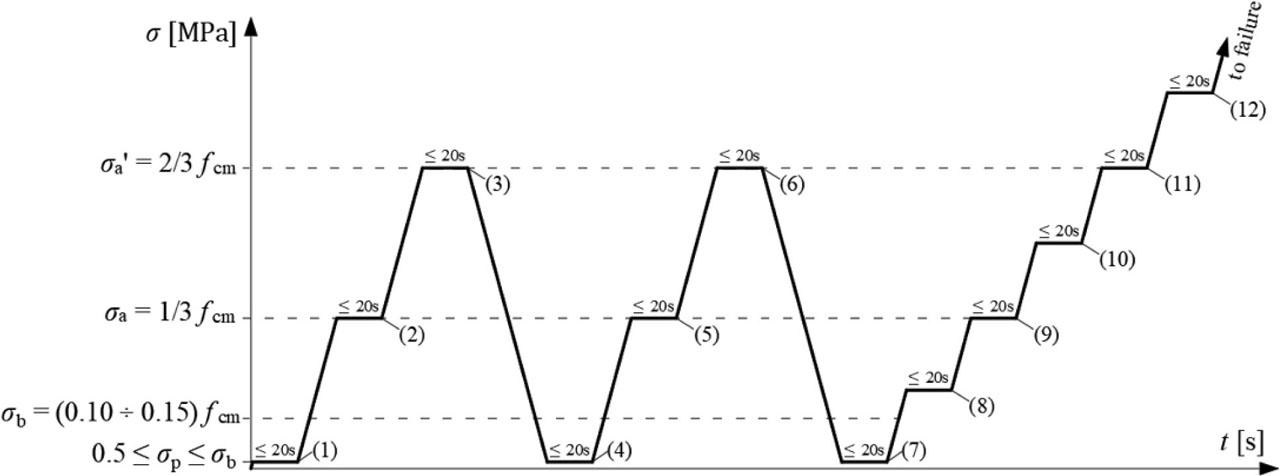
Figure 5

Figure 6

Figure 7
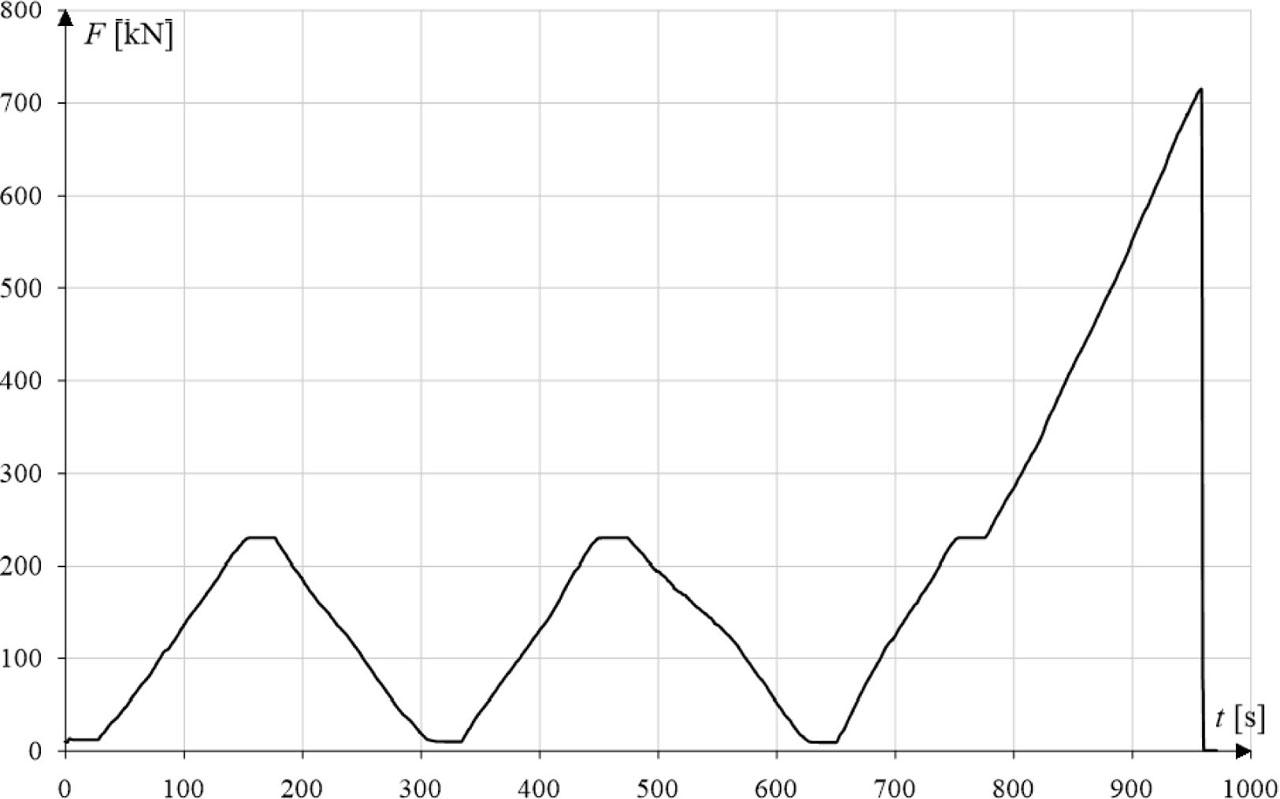
Figure 8
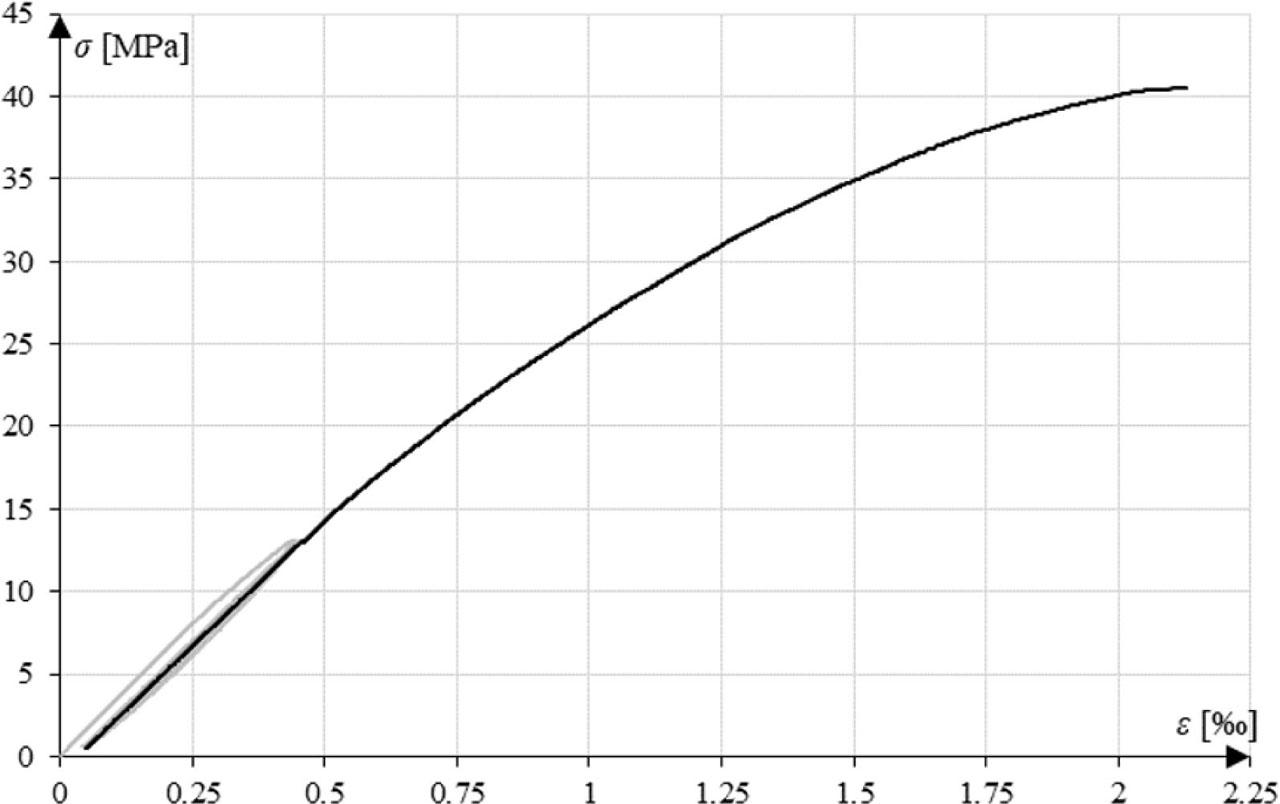
Figure 9
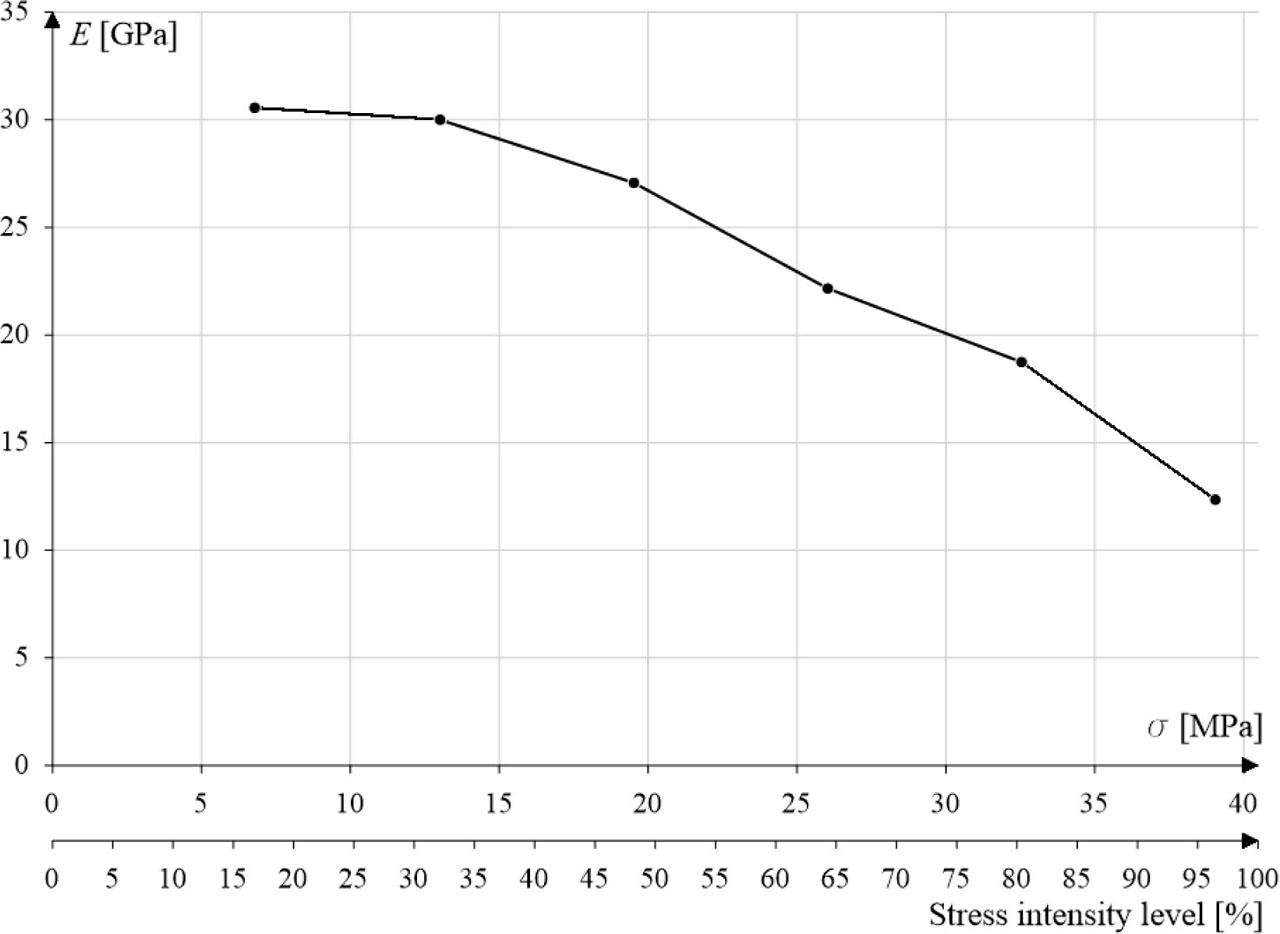
Figure 10
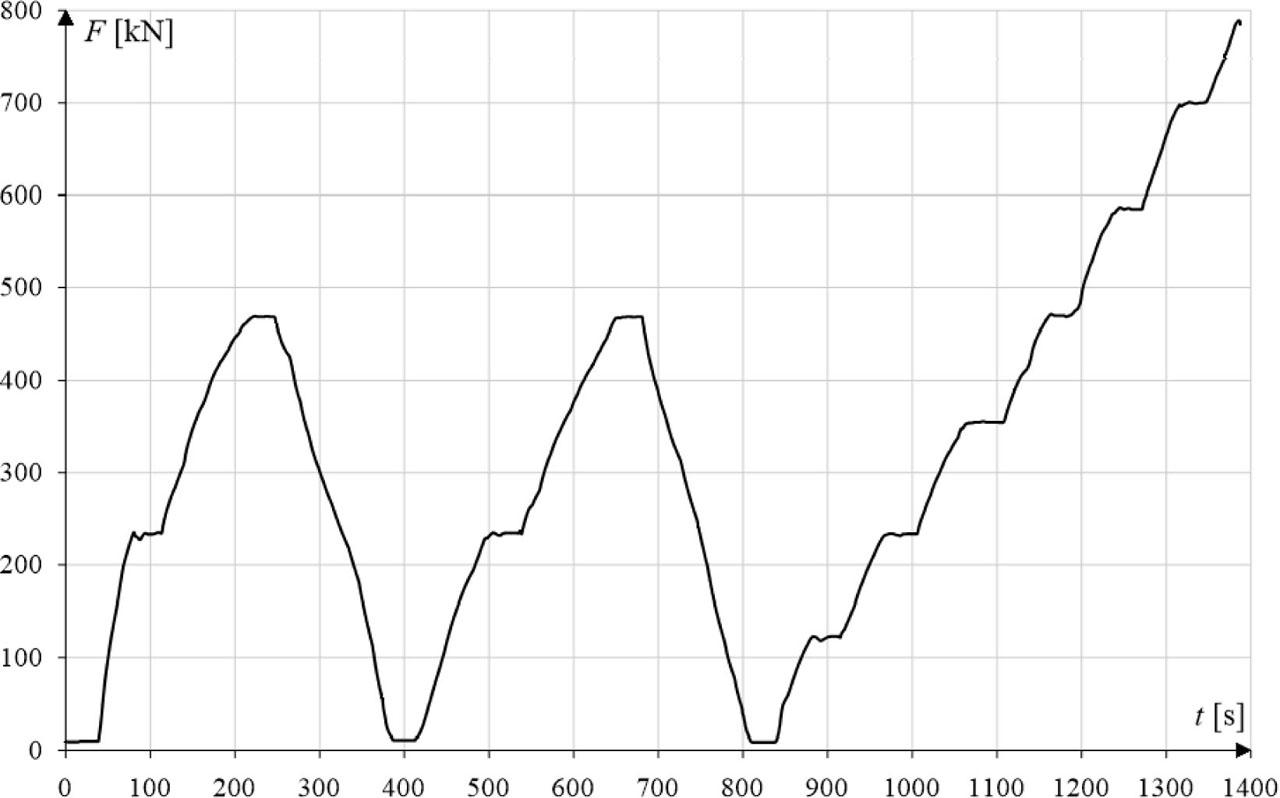
Figure 11
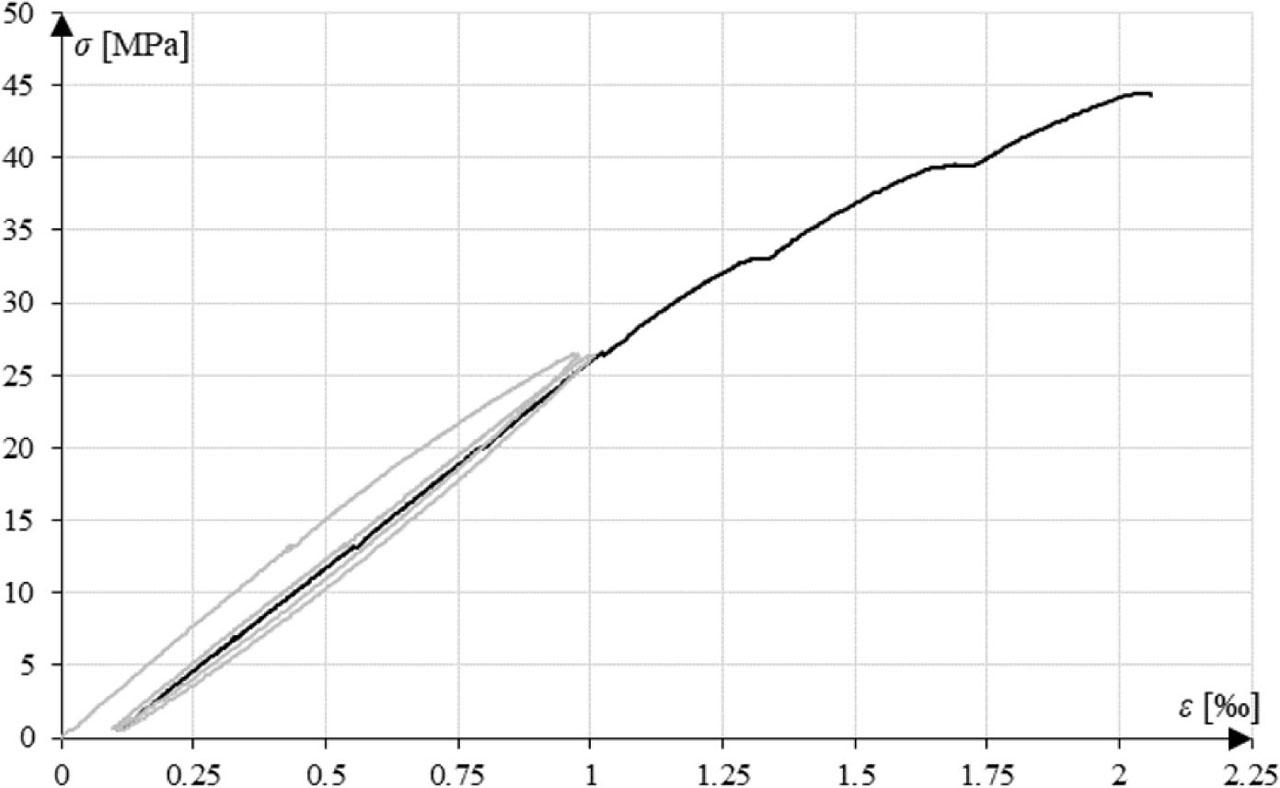
Figure 12
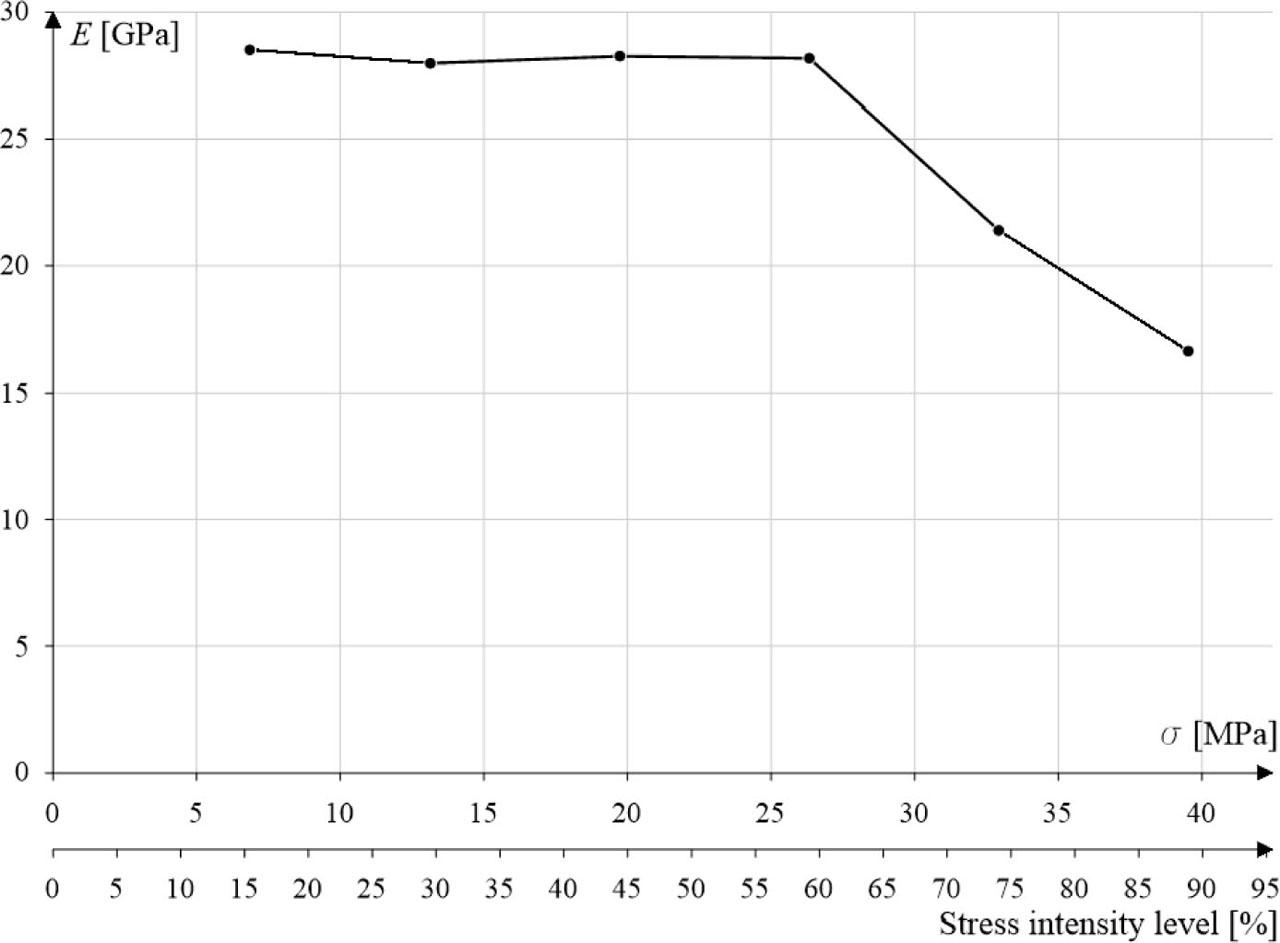
Figure 13

Figure 14
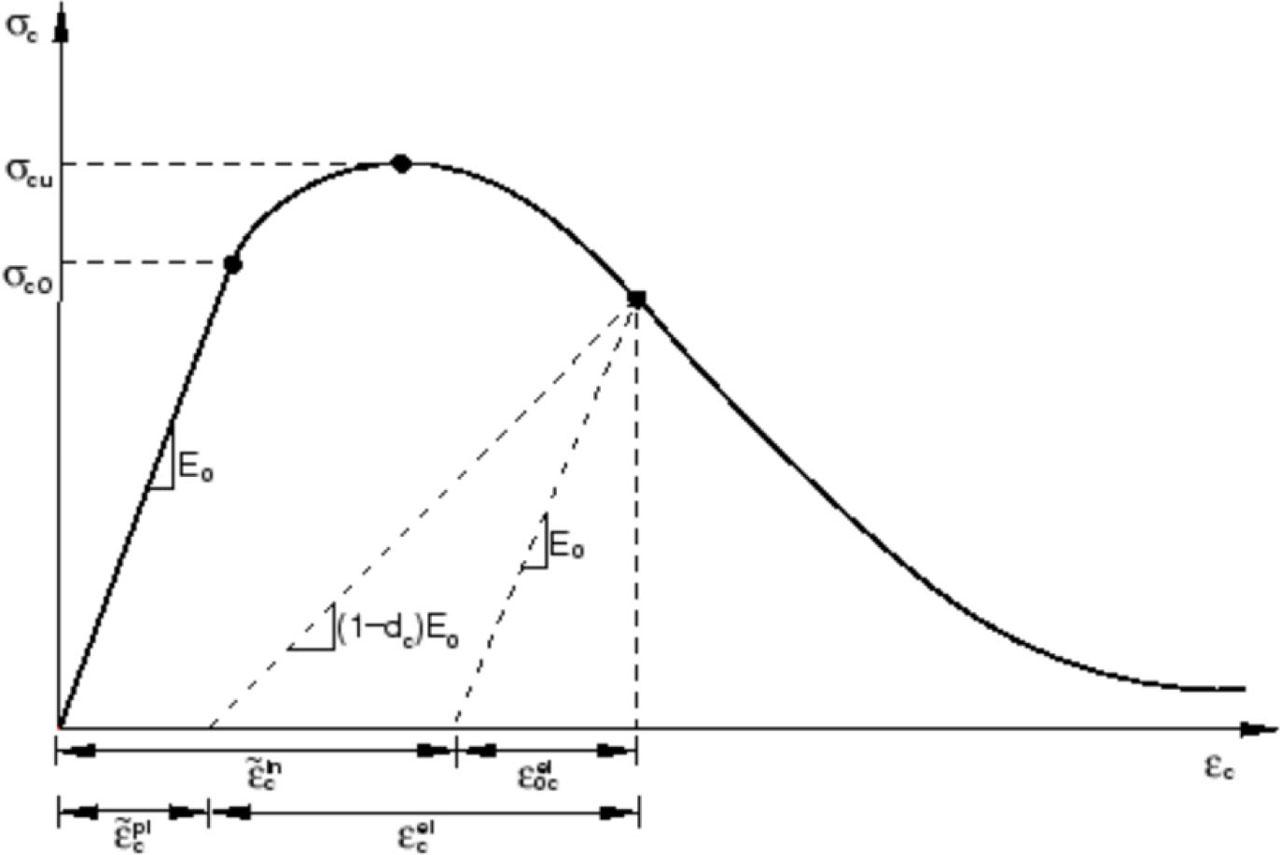
Figure 15
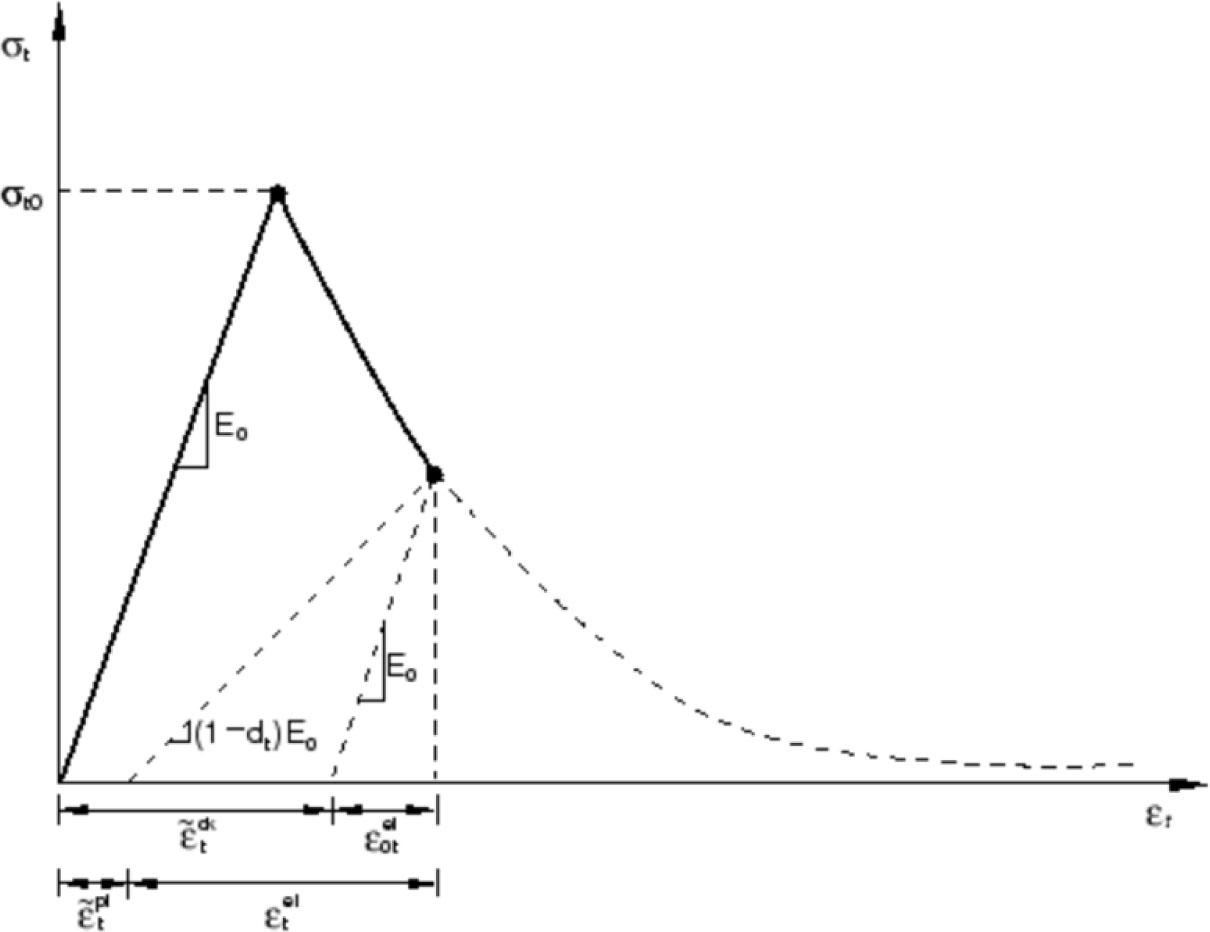
Figure 16
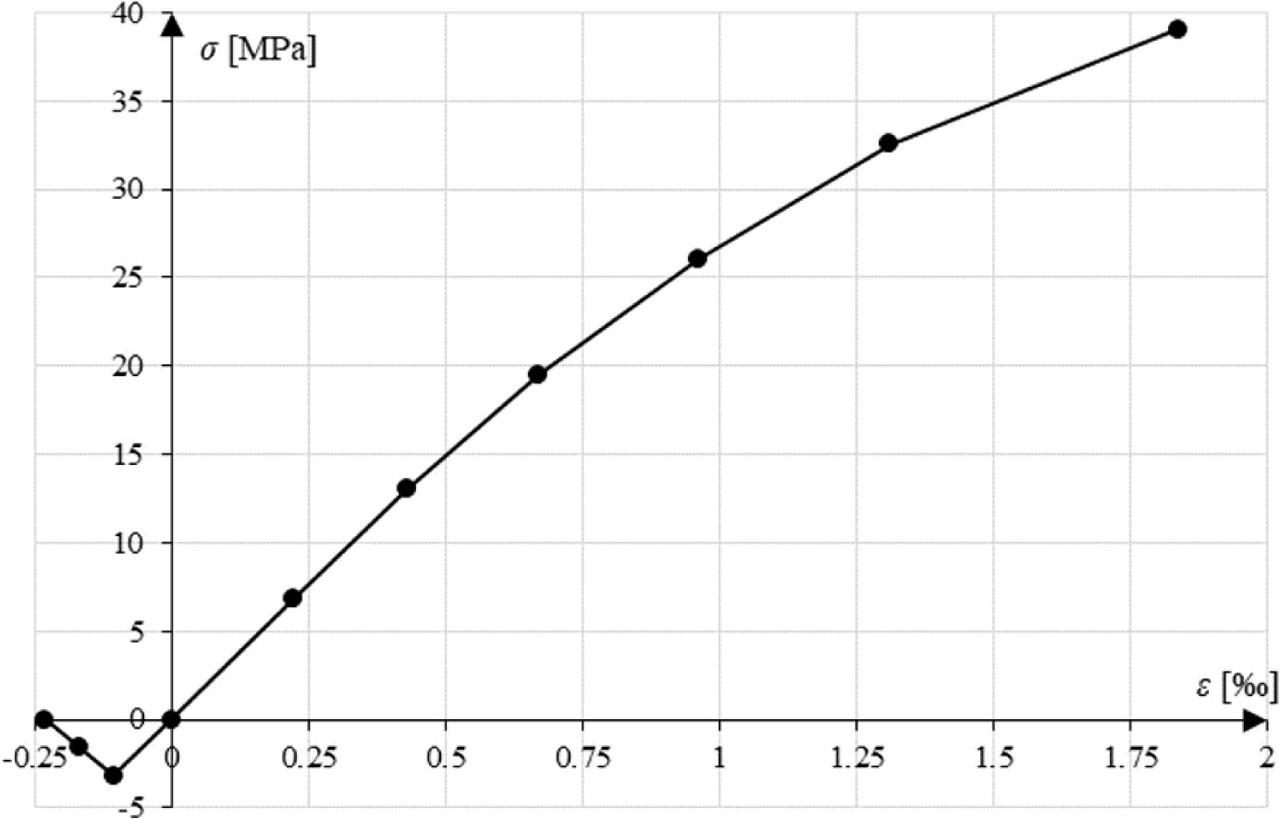
Figure 17

Figure 18
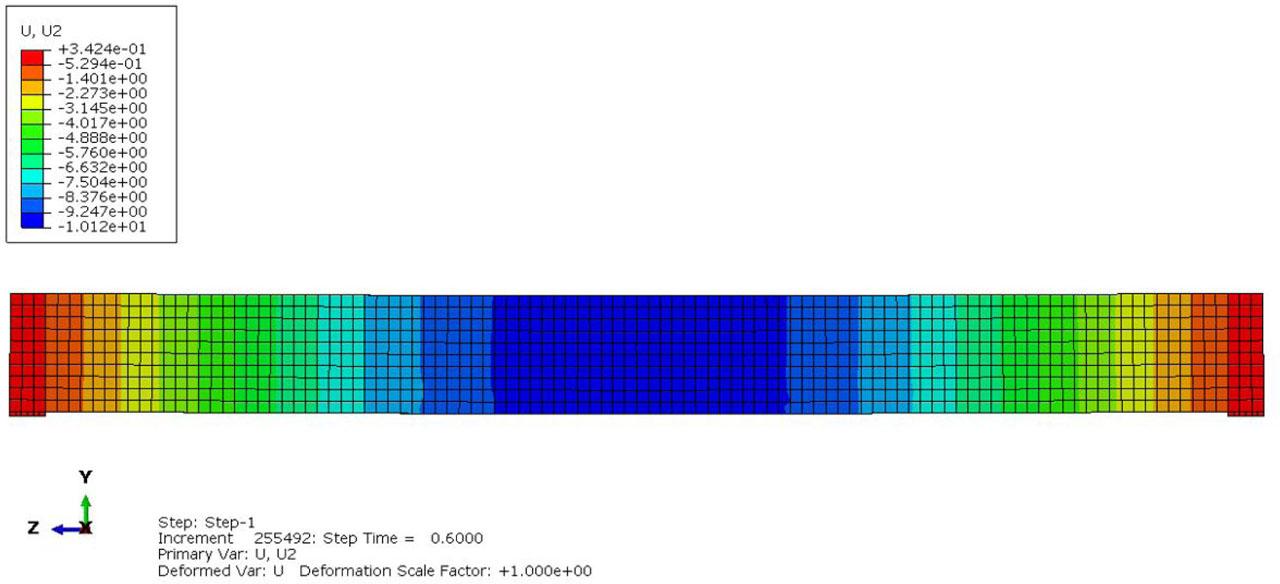
Figure 19
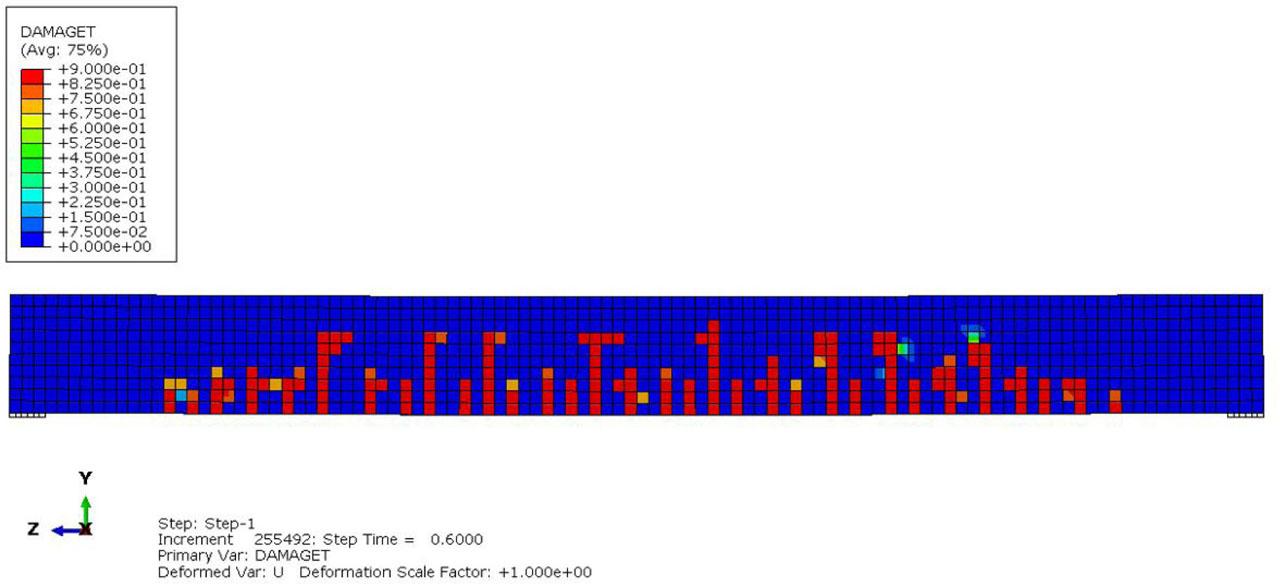
Figure 20

Figure 21
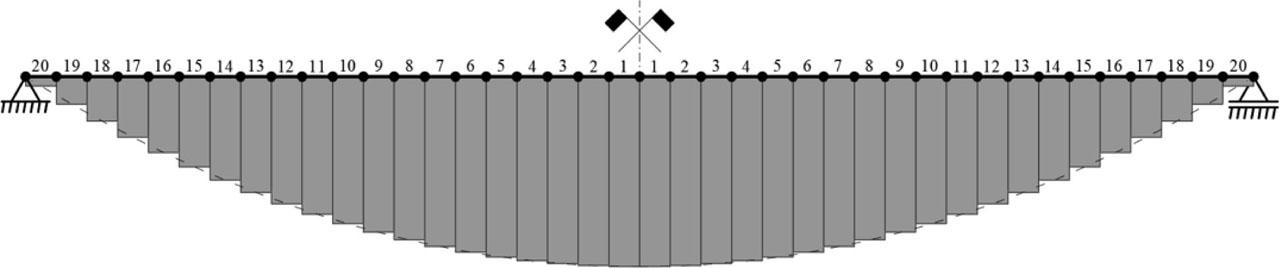
Figure 22
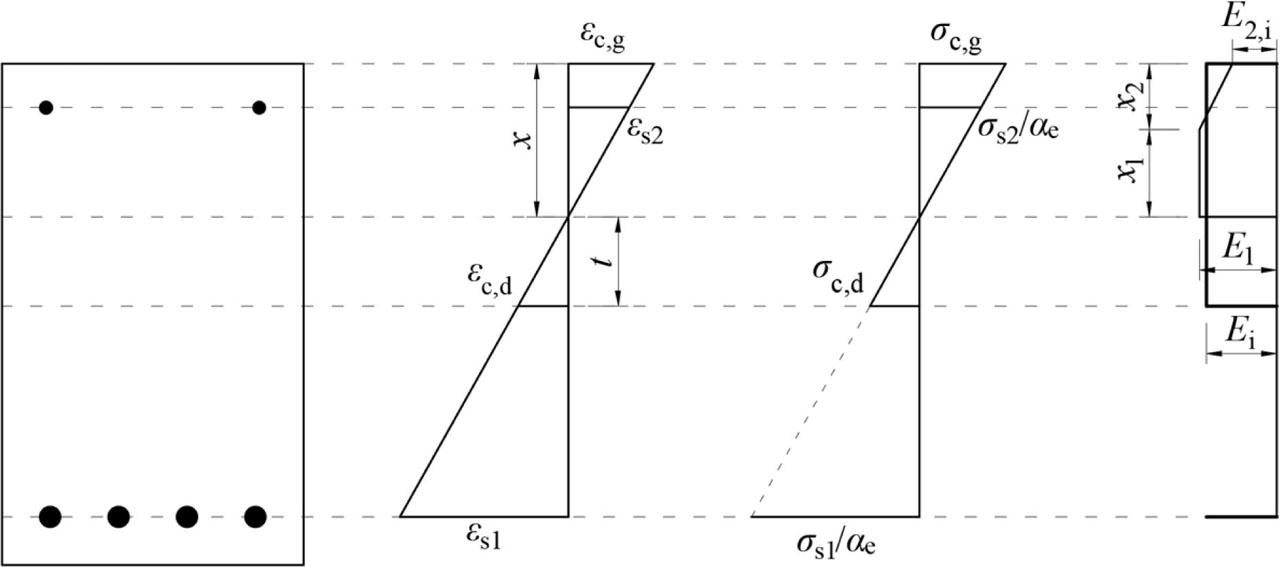
Figure 23
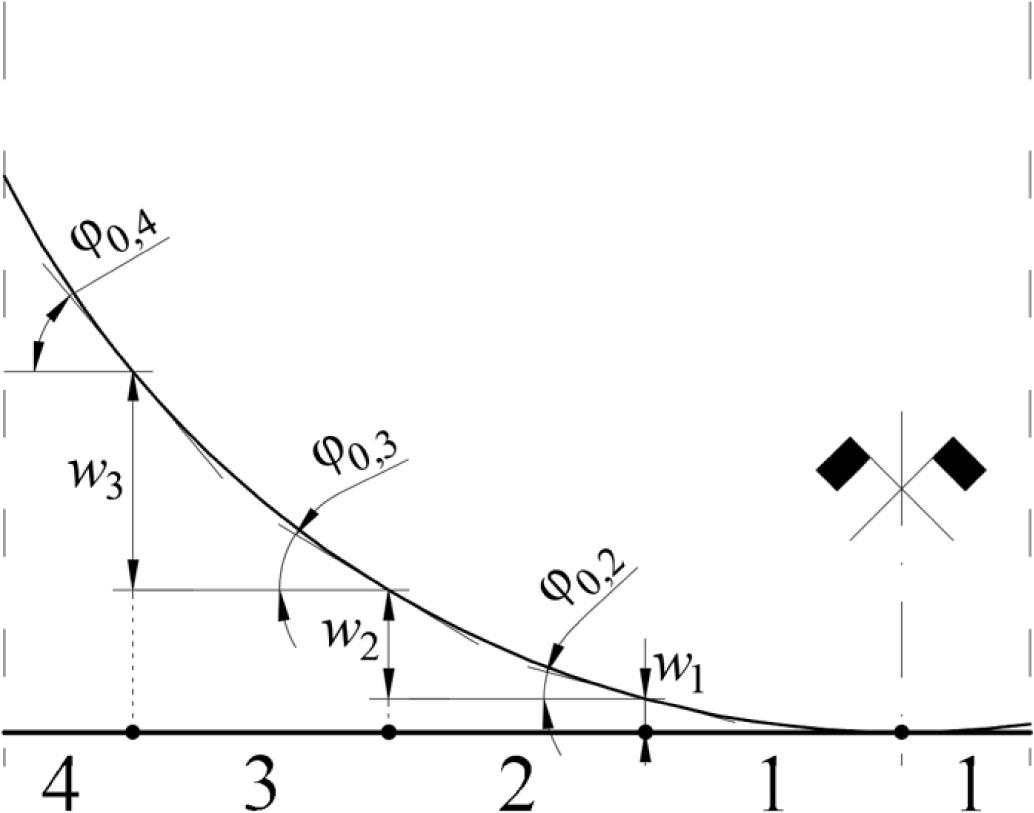
Figure 24
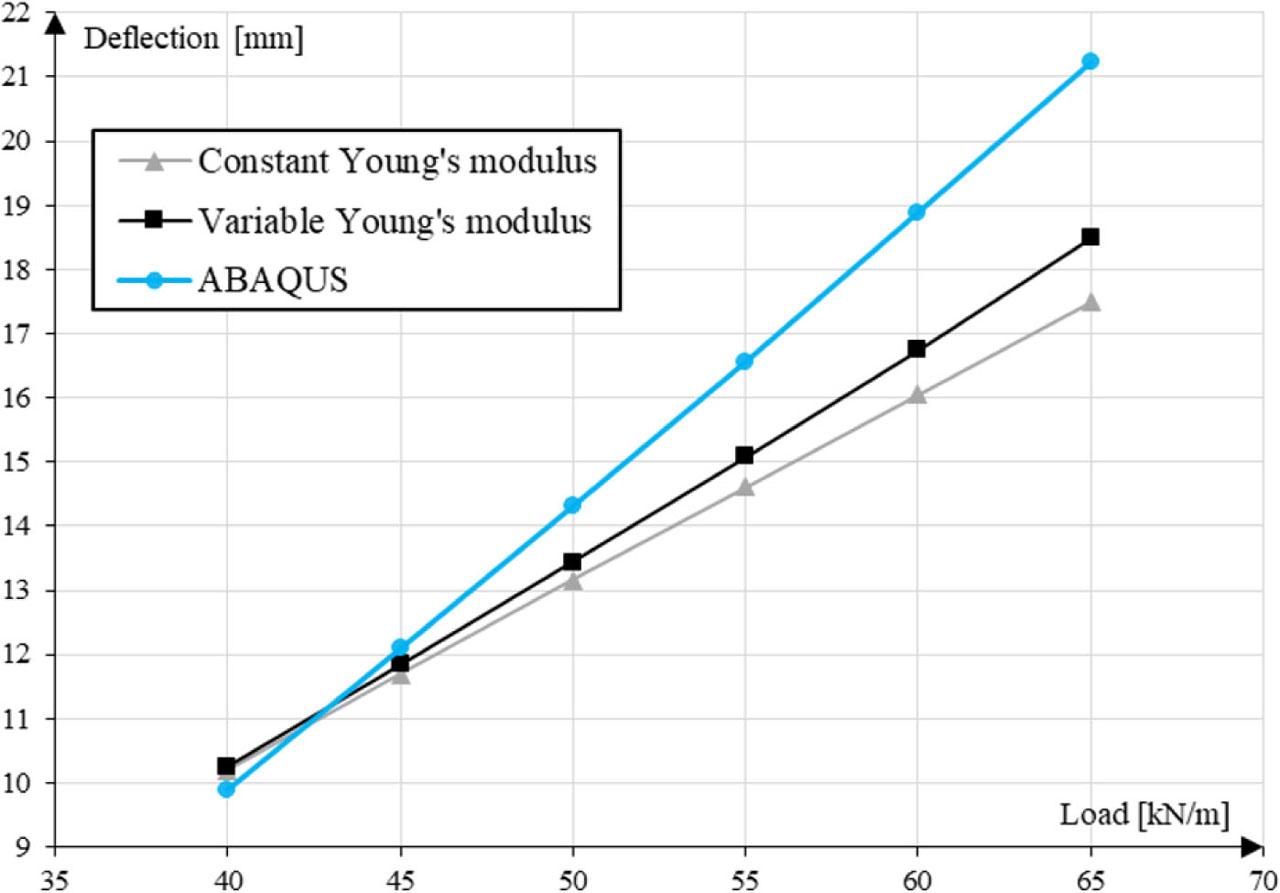
Figure 25
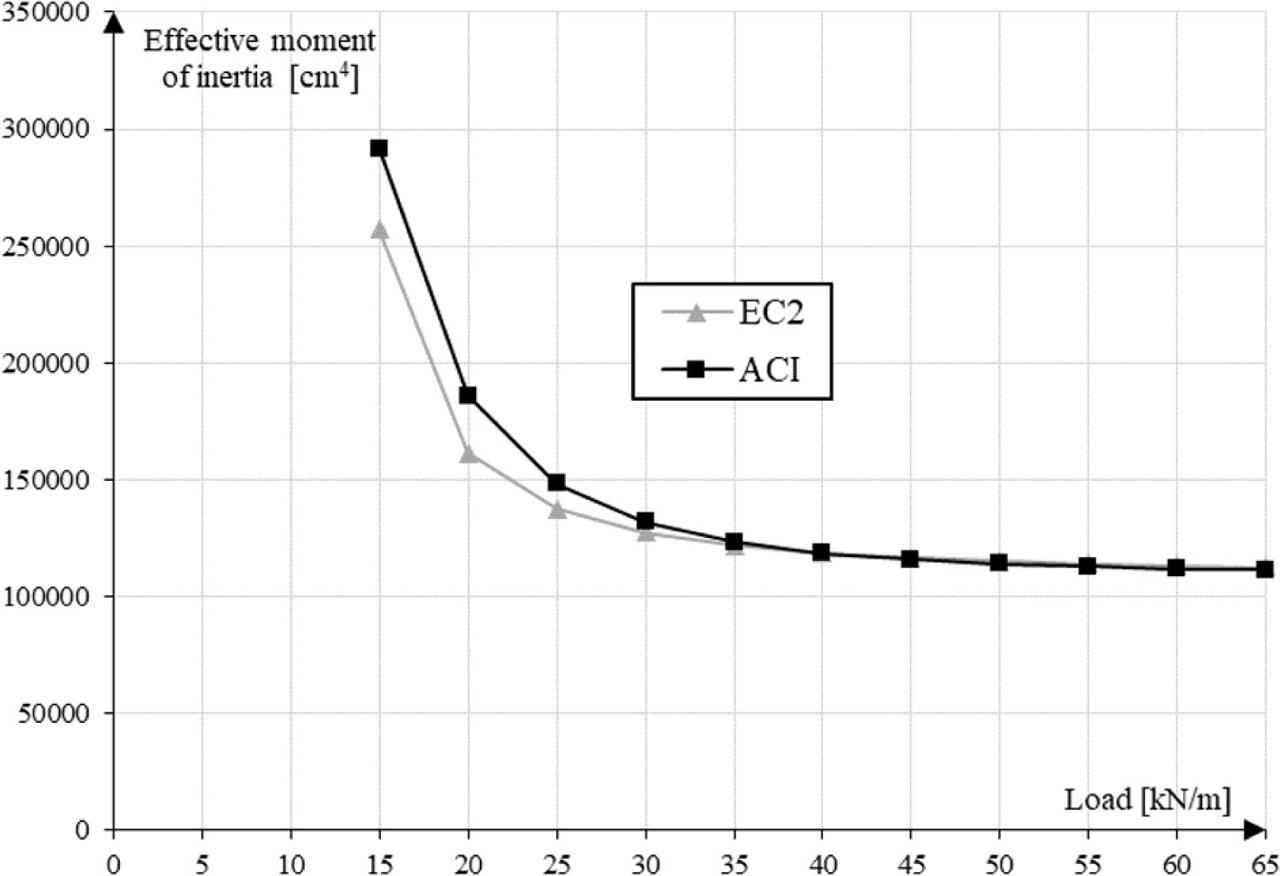
Design of concrete mix used to make tested cylindrical specimens_
| No. | Constituent | Mass |
|---|---|---|
| [kg/m3] | ||
| 1 | Cement CEM I 42.5R | 365.0 |
| 2 | Aggregate 2–8 mm | 650.0 |
| 3 | Aggregate 8–16 mm | 560.0 |
| 4 | Sand 0–2 mm | 650.0 |
| 5 | Water | 175.0 |
| 6 | Superplasticizer (1.2% of cement mass) | 4.5 |
Comparison of beam deflections for constant and variable Young's modulus of concrete_
| No. | Load | Bending effort of the element | Constant Young's modulus | Variable Young's modulus | Relative increment in deflection |
|---|---|---|---|---|---|
| α | α’ | ||||
| [kN/m] | [%] | [mm] | [mm] | [%] | |
| 1 | 40 | 58 | 10.20 | 10.26 | 0.59 |
| 2 | 45 | 66 | 11.69 | 11.84 | 1.28 |
| 3 | 50 | 73 | 13.16 | 13.44 | 2.13 |
| 4 | 55 | 80 | 14.61 | 15.08 | 3.22 |
| 5 | 60 | 88 | 16.05 | 16.75 | 4.36 |
| 6 | 65 | 95 | 17.49 | 18.48 | 5.66 |
Comparison of deflections for bar model and FEM model_
| No. | Bar model | FE model | Relative difference between α〉 and αCDP | ||
|---|---|---|---|---|---|
| Load | Constant Young's modulus | Variable Young's modulus | ABAQUS - CDP | ||
| α | α’ | αCDP | |||
| [kN/m] | [mm] | [mm] | [mm] | [%] | |
| 1 | 40 | 10.20 | 10.26 | 9.90 | 3.51 |
| 2 | 45 | 11.69 | 11.84 | 12.09 | 2.11 |
| 3 | 50 | 13.16 | 13.44 | 14.31 | 6.47 |
| 4 | 55 | 14.61 | 15.08 | 16.57 | 9.88 |
| 5 | 60 | 16.05 | 16.75 | 18.88 | 12.72 |
| 6 | 65 | 17.49 | 18.48 | 21.23 | 14.88 |