As a high-performance inertial navigation sensor, fiber optic gyro (FOG) has gained wide applications in aviation [1][2], aerospace, marine, and transportation fields due to its advantages of all-solid-state design, high sensitivity, small size, and long lifetime, progressively taking the place of the conventional mechanical gyro and becoming the mainstream gyro in the field of inertial navigation [3].
As the core component of the inertial navigation system, the reliability assessment of the fiber optic gyro is of significant importance [4]. Traditional reliability assessment methods, which rely solely on failure life data, focus exclusively on binary product states (normal and failure) [5]. These methods are inadequate for highly reliable, longlife electromechanical products like FOGs, which rarely fail completely but exhibit gradual performance degradation over time. consequently, failure life data alone cannot accurately assess their reliability.
The performance degradation process of FOGs contains substantial reliability information, reflecting their operational characteristics [6][7]. By collecting degradation data and applying degradation analysis theory, this approach effectively addresses reliability assessment challenges. It captures gradual degradation patterns and provides a more accurate evaluation, overcoming the limitations of traditional methods.
Reliability assessment methods based on performance degradation analysis can be categorized into three types [8][9]: degradation trajectory modeling [10], degradation volume distribution modeling [11], and modeling methods based on stochastic processes [12]. Degradation trajectory models are computationally simple and can fit degradation trajectories with limited data. Degradation volume distribution models offer high assessment accuracy and broad applicability, especially when trajectory variations are significant. While both approaches can model the inherent degradation processes of products, they struggle to account for the random environmental impacts on degradation.
In recent years, stochastic process models have been widely adopted to describe the stochastic degradation process of a product under environmental stresses. Among them, the Gamma process and Inverse Gaussian process are suitable for describing systems with strictly increasing degradation [13][14], while the Wiener process is more suitable for modeling non-monotonic degradation processes.
Liu et al. [15] proposed a reliability assessment method combining an artificial neural network and Wiener process, in which both individual differences and measurement error factors were considered to improve the accuracy of reliability assessment. Wang et al. [16] used the Wiener process with dual time scale function as the crack extension model in the reliability assessment of the turbine disk tongue and groove, and estimated the average life span of the turbine disk tongue and groove. Zhu et al. [17] constructed eight reliability evaluation models based on the Wiener process degradation model in describing the performance degradation of lithium-ion batteries, and finally, after validation, proved that the binary stochastic parameter model can evaluate the battery degradation process more accurately.
Although the preceding studies have produced successful results in performance degradation modeling, there are still some shortcomings. For example, the existing methods often require complex model tuning and parameter estimation when dealing with nonlinear degradation trends and individual variability, leading to computational inefficiency. Especially for high-precision devices such as fiber-optic gyroscopes, their performance degradation process is not only affected by individual variability, but also shows obvious nonlinear trends, and it is difficult to accurately describe their actual degradation behaviors by existing methods.
To address the above problems, this paper proposes a Wiener process model based on nonlinear random effects for modeling the degradation process and reliability assessment of fiber optic gyroscopes. Firstly, the zero-bias performance degradation data is selected as the key index for reliability assessment; secondly, based on the traditional Wiener process model, nonlinear random effect is introduced to better describe the actual degradation behavior; subsequently, the Gibbs sampling method is adopted to accurately estimate the parameters of the model; and finally, the validity of the method is proved through experiments.
The composition block diagram of the fiber optic gyroscope is displayed in Figure 1. It is primarily made up of two parts: the circuit part and the optical path part. The optical path part mainly includes the light source, detector assembly, coupler, phase modulator (Y waveguide) and fiber coil, etc. While the circuit part mainly consists of two parts: the light source driving circuit and the signal detection circuit [18].
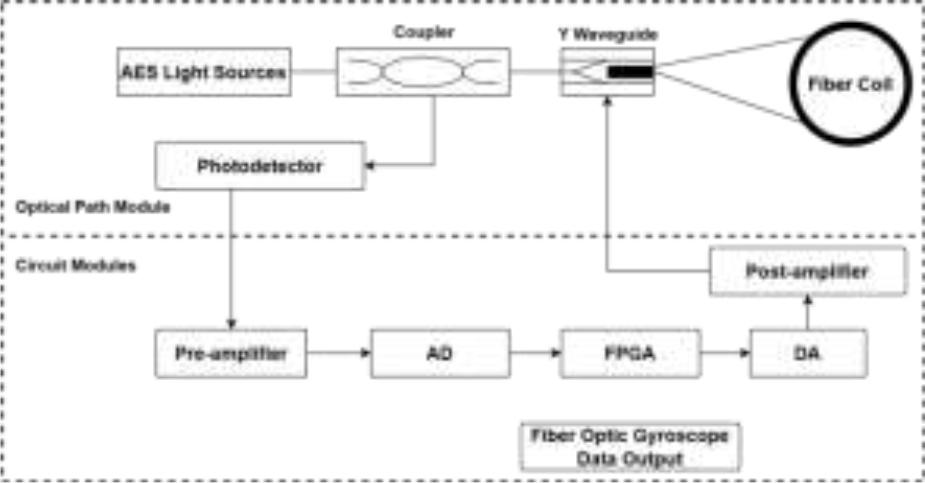
Fiber optic gyroscope composition block diagram
Light in the role of the coupler is divided into two, a beam to the empty end, the other beam is transmitted to the Y waveguide, in which is divided into clockwise and counterclockwise two beams of light, and then into the fiber coil in the direction of the transmission; in the fiber coil in the direction of the transmission of the two beams of light in the Y waveguide at the common end of the meeting, the interference occurs, i.e., the Sagnac effect, interfering with the light through the coupler and then transmitted to the detector assembly, the optical signal is converted into an electrical signal; The electrical signal is amplified, filtered and then converted into a digital signal by A/D, and then processed by the FPGA unit to obtain the angular velocity to which the fiber optic gyro is sensitive, thus realizing the real-time measurement of the carrier's rotational motion.
Among the performance indexes of fiber optic gyro, zero bias is the most important index to measure its reliability. Zero bias refers to the phenomenon that the measurement output of the fiber optic gyro is not zero in the absence of angular input. The key factors affecting zero bias include white noise, scattering noise, relative intensity noise of light source, quantization noise, electrical noise, thermal phase noise, polarization error, nonlinear Kerr effect error, error caused by back reflection, and circuit demodulation drift. With the growth of storage time, the differentiation of light source and optical transmission channel, and the degradation of electronic component performance, the zero bias will gradually show obvious degradation trend. In addition, the zero bias has good observability and is easy to be measured by experiments. In this paper, the zero deviation is selected as a key parameter to study the performance degradation trend of the fiber optic gyro in order to complete the reliability assessment.
The degradation process of fiber-optic gyroscopes is affected by a variety of factors, including external environmental impacts and wear and corrosion of internal components, resulting in a significant randomness in the degradation process. The performance degradation model based on stochastic process can effectively describe this stochastic uncertainty, in the existing research, the Wiener process and the Gamma process are consistent with the infinitely divisible characteristics of the device performance degradation, and can characterize the device degradation by the accumulation of small random events. The Gamma process has monotonicity, which is suitable for monotonous degradation process, while the Wiener process is suitable for describing the degradation process with The Gamma process is monotonic and suitable for monotonic degradation processes, while the Wiener process is suitable for describing degradation processes with continuous fluctuations. Therefore, the Wiener process can be used to model the degradation of each performance of the fiber optic gyro, and its performance degradation amount model X(t) is expressed as shown in Equation (1).
Where: X(t) represents the performance degradation of the fiber optic gyro at the moment t, and μ denotes the drift coefficient of the degradation of the performance parameter, which describes the degradation rate of the performance degradation of the fiber optic gyro. σ denotes the diffusion coefficient of the amount of degradation of the performance parameter, characterizing the effect of random factors on the performance of the fiber optic gyro; B (▯) is a standard Brownian motion process characterizing the random fluctuation properties of the degradation process.
According to the definition of Wiener process, the degenerate process X(t) shown in (1) has the following basic properties.
- 1)
X (0) = 0, and X(t) is continuous at t =0.
- 2)
{X(t), t ≥ 0} has smooth independent increments, i.e., the increments are independent of the time starting point.
- 3)
The degenerate increment ΔX(t) follows a normal distribution, i.e. ΔX(t) ~ N(μ△t, σ2△t). The probability density function for the increment ΔX(t) in performance degradation can be expressed as (2).
Assuming that the performance degradation process of the fiber optic gyroscope obeys the Wiener process {X(t), t≥0}, The failure threshold is ξ.The lifetime T of the gyro is the time at which the gyro degradation volume first reaches the failure threshold (first reach time), expressed as shown in (3):
Let μ and σ be fixed unknown parameters, and the product lifetime T follows an Inverse Gaussian distribution. Its probability density function is given by (4):
The corresponding lifetime distribution function is given by (5):
Where Φ(▯) is the standard normal distribution function.
The reliability of the fiber optic gyroscope can then be expressed as (6):
Individual fiber optic gyroscopes within the same batch exhibit unit-to-unit variability due to factors such as machining errors during manufacturing, assembly tolerances, and material differences. These variations lead to differing degradation rates among units, even under identical experimental conditions. Therefore, when modeling the degradation of test samples, it is essential to account for individual differences to better align with real-world scenarios.
Additionally, the degradation data of fiber optic gyroscope performance metrics often exhibit nonlinear characteristics rather than purely time-linear relationships. Using a standard Wiener process for modeling may result in deviations from actual behavior. In such cases, a nonlinear stochastic Wiener process with random effects is more appropriate for capturing these complex degradation trends.
The nonlinear degradation data is characterized by a nonlinear relationship between the performance degradation measure X(t) and time t. To address this, the time scale can be transformed to convert their nonlinear relationship into a linear one. The time-scale model is expressed as (7):
Individual variability can be reflected through differences in performance degradation rates. The parameter μ describing the degradation rate is transformed from a constant to a random variable. Assuming μ follows a normal distribution
Given that μ is a random variable following
As previously derived, the probability density function f(t | μ, σ2) without considering individual differences is given by (4).Based on the law of total probability and conditional probability methods, the probability density function of the nonlinear Wiener process considering individual variability can be expressed as (10).
The corresponding lifetime distribution function can be expressed as (11):
It can be deduced that the reliability function describing the degradation of the system is expressed as (12):
In the standard Wiener process, there are two unknown parameters to be estimated: μ and σ. Based on the probability density function given by (2), the likelihood function for the standard linear Wiener process can be derived as (13):
In the nonlinear Wiener process with random effects, there are four unknown parameters to be estimated, denoted as the parameter vector: θ = {μβ, σβ, σ, a}. and the likelihood function can be expressed as (14):
In the equation, △x(ti,j) = x(ti,j–1) represents the performance degradation increment, and △Λ(ti,j) = Λ(ti,j) – Λ(ti,j–1) denotes the time increment.
As the number of parameters increases, the complexity of the model also rises. Traditional parameter estimation methods, such as maximum likelihood estimation and least squares, often require computationally intensive integral calculations when handling multiple parameters. This becomes particularly challenging or even infeasible when redundant parameters (i.e., parameters with negligible effects on results or high correlation with other parameters) exist in the model. To address this issue, this study adopts the Bayesian theory-based Markov Chain Monte Carlo (MCMC) method. The MCMC method avoids complex integral calculations by simulating samples directly from the posterior distribution, making it suitable for estimating multi-parameter models. Compared to traditional methods, the MCMC approach offers the following advantages:
- 1)
No complex integrals required: Samples are generated directly through sampling, eliminating the need for integral computations;
- 2)
High adaptability: Capable of handling intricate models and diverse prior distributions;
- 3)
Reliable results: Ensures estimation accuracy through multi-chain diagnostics.
The Bayes' theorem embodies the core concepts of Bayesian theory and the fundamental principles of Bayesian estimation. Its mathematical formulation is presented in (15):
In the equations,
π(θ|x) represents the posterior distribution of the parameter θ, reflecting the updated understanding of θ after observing the data x;
π(θ) denotes the prior distribution of θ, representing the initial belief about θ before incorporating the observed data;
f(x|θ) is the likelihood function of the random variable x, quantifying the probability of observing the data x given the parameter θ;
m(x) is the marginal distribution, which normalizes the posterior distribution to ensure it integrates to unity.
From the equation above, it is evident that Bayesian theory treats each experimental result as new information about the parameters, integrates this new information with prior knowledge available before the experiment, and updates the parameter estimates, thereby bringing the results closer to the true values. The entire process can be viewed as a continuous refinement of the parameter θ being estimated. The procedure for parameter estimation based on Bayesian theory is illustrated in Figure 2.
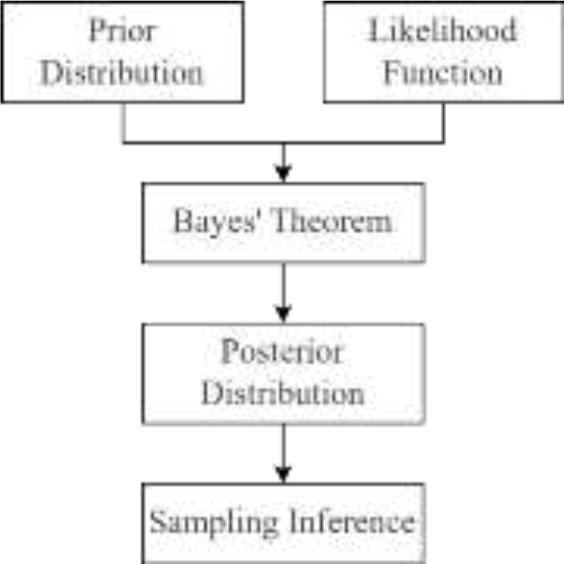
Parameter estimation process based on Bayesian theory
- 1)
Specify the prior distribution: Determine the prior distribution π(θ) of the parameter θ based on its prior information;
- 2)
Construct the likelihood function: Derive the likelihood function f(x|θ) for the sample x = (x1, ⋯, xn), as shown in (16):
16 - 3)
Obtain the posterior distribution: Calculate the posterior probability density function of the parameter θ by combining the prior distribution π(θ) and the likelihood function f(x|θ) using Bayes' theorem.
- 4)
Sampling and inference: Generate samples from the posterior distribution through MCMC or other sampling methods to perform parameter estimation and statistical inference.
The MCMC algorithm generates simulated samples of parameter vectors directly from the posterior distribution through numerical simulation. Common MCMC algorithms fall into two categories: The Metropolis-Hastings algorithm and the Gibbs sampling algorithm. The efficiency of the Metropolis-Hastings algorithm depends on the similarity between the chosen proposal density function and the true posterior density function. In contrast, the Gibbs sampling algorithm avoids this issue, as it imposes less stringent requirements on the proposal density function while achieving higher computational efficiency. In practical applications, the MCMC-Gibbs sampling process can be implemented using software packages such as OpenBUGS and WinBUGS.
The Gibbs sampling algorithm is implemented as follows; given the parameter vector θ = (θ1, θ2, ⋯, θq) and observed data data = (data1, data2, ⋯, datan), with the posterior distribution p(θ1| θ2, ⋯, θq, data):
- 1)
Assign initial values: Set an initial parameter vector
- 2)
Sample from conditional distributions: Sample
- 3)
Complete one iteration: Repeat 2) until
- 4)
Iterate: Repeat steps 2)-3) for m iterations to obtain
When m is sufficiently large, θ(m) can be considered as samples drawn from the posterior p(θ|data), enabling the estimation of unknown parameters.
For the degradation test data, when there are multiple degradation models to choose from, it is necessary to select the model that fits the degradation data the best, and Akaike information criterion (AIC) is usually used for the model optimization, and the likelihood ratio test is used to judge whether a simple model can be used in place of a complex model.
The AIC criterion is proposed by Akaike, a Japanese statistician, which evaluates the model fit in terms of the value of the likelihood function to measure the degree of fit and the number of unknown parameters in the model, which is the weighted value of the value of the likelihood function and the number of parameters. The smaller the value of the AIC, the better the model fit, and the formula is shown in (17):
In order to visually compare and verify the reasonableness of the model, Quantile-Quantile(Q-Q) Plot is introduced as a visualization tool to assess the degree of fit between the sample data distribution and the theoretical distribution (e.g., normal distribution), as shown in Figure 3. which is a sample Q-Q Plot generated based on the sample of normal distribution, which can be used to illustrate how to assess the degree of fit between the sample data distribution and theoretical The degree of fit to the normal distribution. Data points close to the diagonal line indicate a good fit to the distribution, and in the Q-Q plot, the horizontal axis corresponds to the quantiles of the theoretical distribution, while the vertical axis shows the quantiles of the sample data.
Example of a Q-Q plot
Ideally, the data points should be close to the diagonal distribution, indicating that the sample distribution matches the theoretical distribution; if they deviate, they reflect distributional differences, e.g., tail deviations may point to long-tailed distributions or extremes, whereas center deviations may indicate distributional skewness. The combination of Q-Q plots and AIC criterion can comprehensively assess the distributional hypotheses and provide strong support for the model fit goodness-of-fit tests.
The following section integrates the fiber optic gyroscope's zero-bias degradation data with the simulation verification of the proposed method. The following figure shows the zero-bias performance degradation data of a fiber-optic gyroscope collected in the constant temperature stress accelerated degradation test, in which the constant temperature stress of the fiber-optic gyroscope is controlled to be 55°C, and three fiberoptic gyroscopes of the same model equipped in an inertial platform are selected. During the test, the performance degradation data of zero bias of each sample of fiber-optic gyroscope were tested and recorded over the course of 25 times, with a recording interval of 168h, and a total test time of 4032h, and no failure occurred. The curves of each performance parameter of the fiber optic gyroscope over time are obtained after the test, as shown in Figure 4.
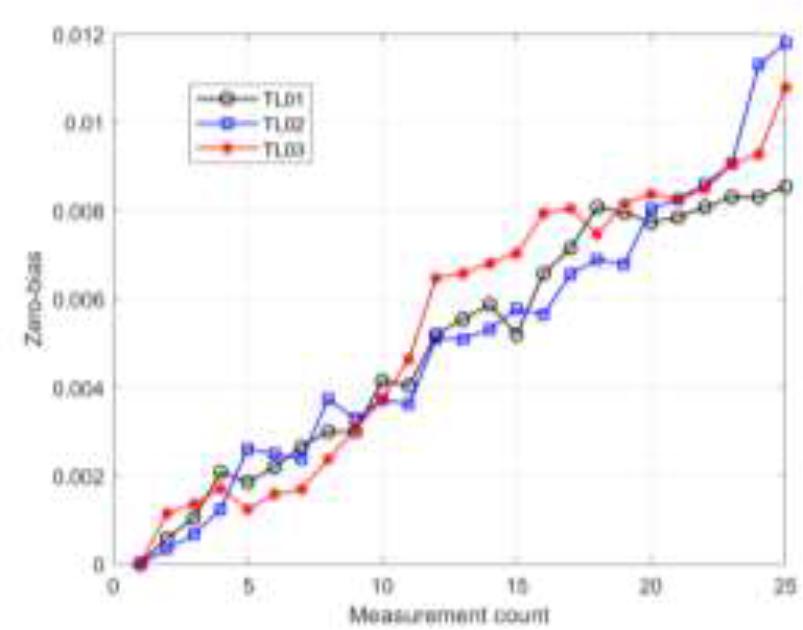
Zero-bias degradation data
Based on specific application requirements, the failure threshold was determined as 0.1°/h. Over time, the zero-bias performance metrics of the three fiber optic gyroscopes (FOGs) exhibited a gradual increase, demonstrating an irreversible overall trend. This upward trend in values indicates a decline in FOG accuracy, reflecting cumulative damage under long-term thermal stress and characterizing the performance degradation of FOGs. Furthermore, the performance degradation data of the three FOG samples showed increased variability with prolonged time, highlighting growing inter-sample performance differences due to individual variations and stochastic factors.
The Wiener process model established in this paper describes a performance degradation process with nonlinearity and individual variability, which aligns with the observed characteristics of the degradation data. This consistency confirms the rationality of employing the Wiener process to model FOG performance degradation. For comparative validation of model feasibility and accuracy in reliability assessment, the standard Wiener process model is designated as M1, while the degenerate model with a nonlinear random effect Wiener process is denoted M2 in subsequent discussions.
First, under the standard Wiener process model M1, the prior distributions of the parameters are set as follows:
In the OpenBUGS software, the MCMC-Gibbs sampling method was employed to generate three Markov chains. Each chain draws 40,000 samples from the posterior distribution to ensure convergence and robustness. TABLE I. lists the statistical measures of the parameter estimates for Model M1, including the mean and standard deviation. The use of multiple chains aims to assess model convergence and validate the stability of parameter estimates by comparing results across different chains.
MCMC
| Parameter | Mean | Standard Deviation | MC Error | 95% credible interval |
|---|---|---|---|---|
| μ | 2.574E-6 | 4.022E-7 | 1.142E-9 | (1.782E-6,3.376E-6) |
| σ | 5.725E-4 | 4.868E-5 | 1.516E-7 | (4.87E-4,6.776E-4) |
The convergence diagnostics for the parameters of Model M1 are illustrated in Figure 5. The figure displays the results of the Gelman-Rubin diagnostic (BGR diagnostic), which was used to evaluate the convergence of parameters (μ and σ) across three independent MCMC chains. In the figure, all BGR values of the chains are close to 1, indicating minimal differences between chains and consistent within-chain and between-chain variances. This demonstrates that the MCMC sampling for parameters μ and σ has converged, and the simulation results are reliable.
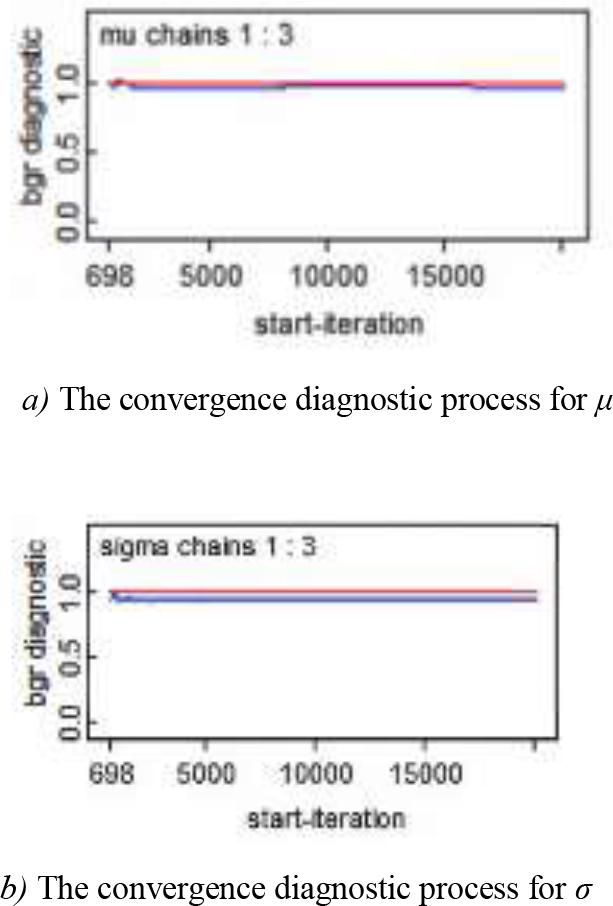
Diagnostic results of convergence of model M1 parameters
Next, under the nonlinear random-effects Wiener process Model M2, the prior distributions of the parameters are specified as follows:
In the OpenBUGS software, the MCMC-Gibbs sampling method was employed with random initial values assigned to parameters to generate two Markov chains. Each chain drew 40,000 samples from the posterior distribution to obtain parameter estimates. TABLE II. lists the mean, standard deviation, and other statistical measures of the parameter estimates for Model M2.
MCMC
| Parameter | Mean | Standard Deviation | MC Error | 95% credible interval |
|---|---|---|---|---|
| μμ1 | 6.79E-4 | 5.059E-5 | 2.316E-7 | (5.815E-4,7.817E-4) |
| σβ1 | 4.455E-5 | 6.103E-6 | 3.656E-8 | (2.793E-5,4.987E-5) |
| σ1 | 8.551E-4 | 3.427E-5 | 1.356E-7 | (7.732E-4,8.983E-4) |
| a1 | 0.7467 | 0.003256 | 1.766E-5 | (0.738,0.7499) |
The convergence diagnostics for the parameters of Model M2 are illustrated in Figure 6. The figure displays the results of the Gelman-Rubin diagnostic (BGR diagnostic), which was used to evaluate the convergence of parameters μβ1, σβ1, σ1, a1 across two independent MCMC chains.In the figure, all BGR values for the parameters rapidly approach and stabilize near the ideal value of 1.0, indicating consistent distributions across sampling chains and robust convergence. This demonstrates that the MCMC sampling for parameters μα1, σβ1, σ1, a1 has successfully converged, with no significant discrepancies in the sampling process. Consequently, the model results are reliable, and the posterior distributions of the parameters are credible.
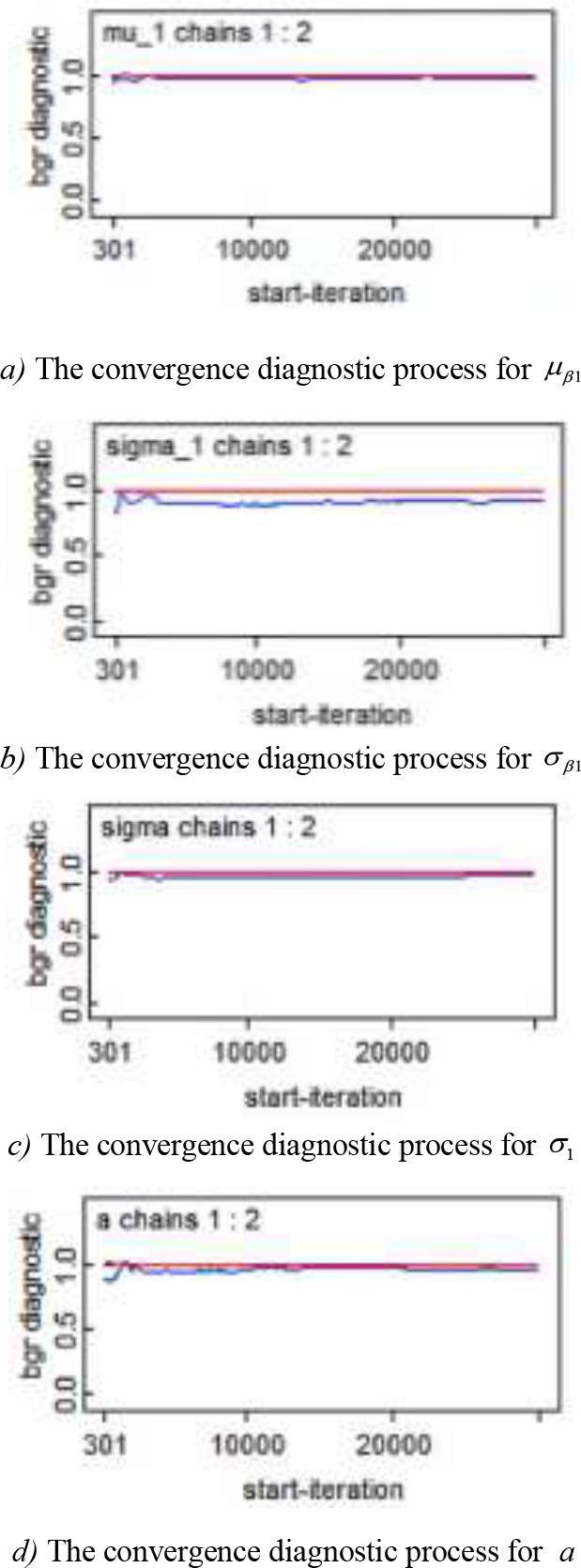
Diagnostic results of convergence of model M2 parameters
As shown in Figure 5. and Figure 6., the parameters of both models M1 and M2 exhibit good convergence. By substituting the parameter estimates from TABLE I. and TABLE II. into (13) and (14), respectively, the log-likelihood values ln(L(θ)) and AIC values can be derived, as summarized in TABLE III. These metrics are used to compare the goodness-of-fit and complexity of the two models.
| Model | ln(L(θ)) | AIC |
|---|---|---|
| M1 | -286.1956 | 576.3911 |
| M2 | -201.5358 | 411.0715 |
From the comparison of M1 and M2 in TABLE III., it is evident that model M2 exhibits a larger log-likelihood value and a smaller AIC value. This suggests that model M1 performs relatively poorly, as its ability to describe the data is either insufficient or overly complex. In contrast, model M2 provides a better fit for the data while simultaneously maintaining lower model complexity. Thus, model M2 is clearly superior to M1.
The Q-Q plots of models M1 and M2 are given in Figure 7. According to the definition of Q-Q plots, it can be seen that the stronger the linear relationship of Q-Q plots, the better the fit of the model.
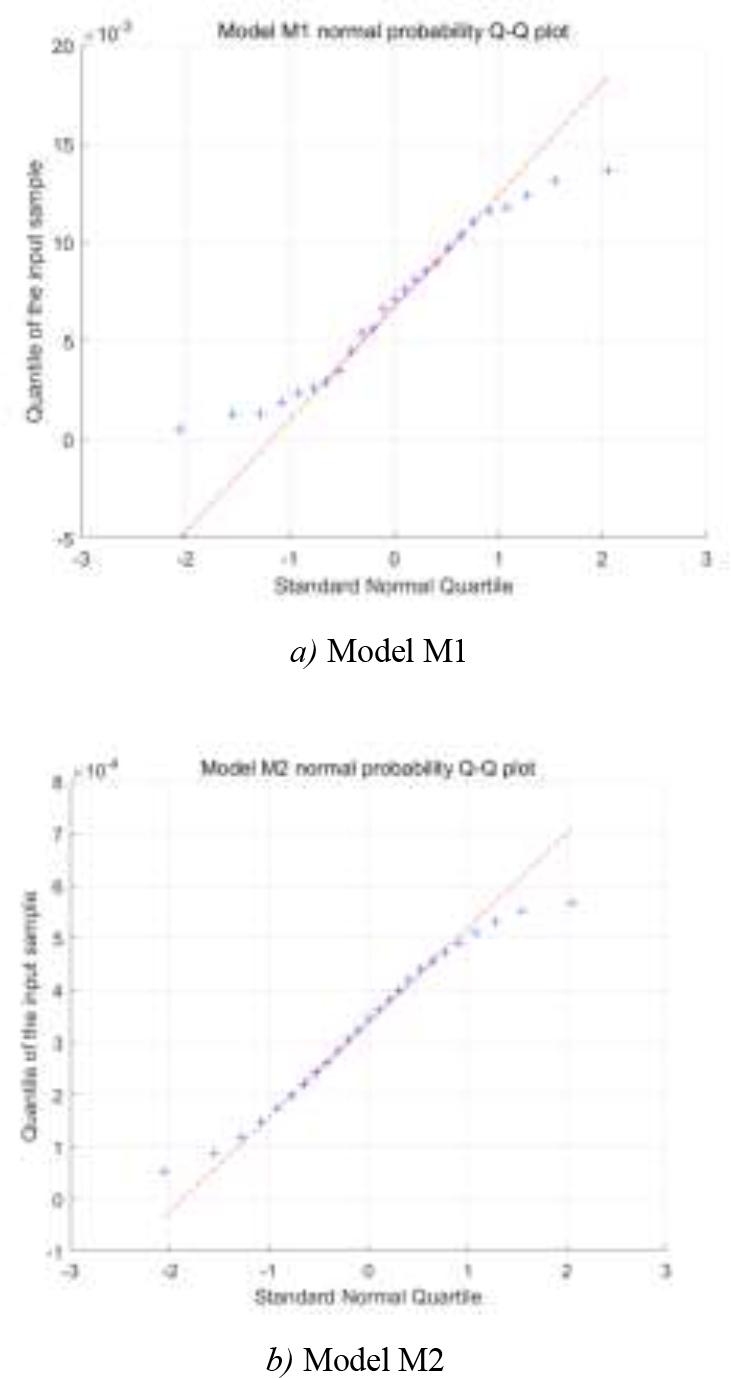
Comparison results of Q-Q plots for M1 and M2
From an analysis of the Q-Q plots of the two models presented in Figure 7., it can be seen that the data points in the Q-Q plot of Model M1 are generally distributed along the red dashed line (the theoretical quantile of the normal distribution), but the deviation is more pronounced, especially in the tail data on the left and the right. The deviation from the theoretical quantile in the tail data suggests that there may be some non-normality in the data for model M1. The data points fit better in the middle region, but the overall fit is poor. The Q-Q plot of model M2 has data points closer to the red dashed line, especially in the middle and tail regions, and the fit is significantly better than that of model M1. the smaller deviation of the tail data from the theoretical quantile suggests that the data distribution of model M2 is closer to the normal distribution. Overall, both models M1 and M2 can describe the degradation process of the fiber-optic gyroscope, which verifies the reasonableness of the modeling. Among them, the Q-Q plot of model M2 shows a stronger linear trend and the data points are closer to the theoretical normal distribution, so M2 is more suitable for describing the zero-bias degradation process of the fiber optic gyro.
Combined with the specific application conditions of the fiber optic gyro in the test, the failure threshold of the performance parameters is determined to be zero bias (≥0.1°/h). By substituting the estimated values of the parameters and the failure thresholds of the performance parameters of the models M1 and M2 into the (6) and (12), the zero-bias reliability curves of the fiber optic gyro's performance parameters based on the standard linear Wiener process and the zero-bias reliability curves of the fiber optic gyro's performance parameters based on the non-linear random effects of the Wiener process are obtained, which are shown in Figure 8.
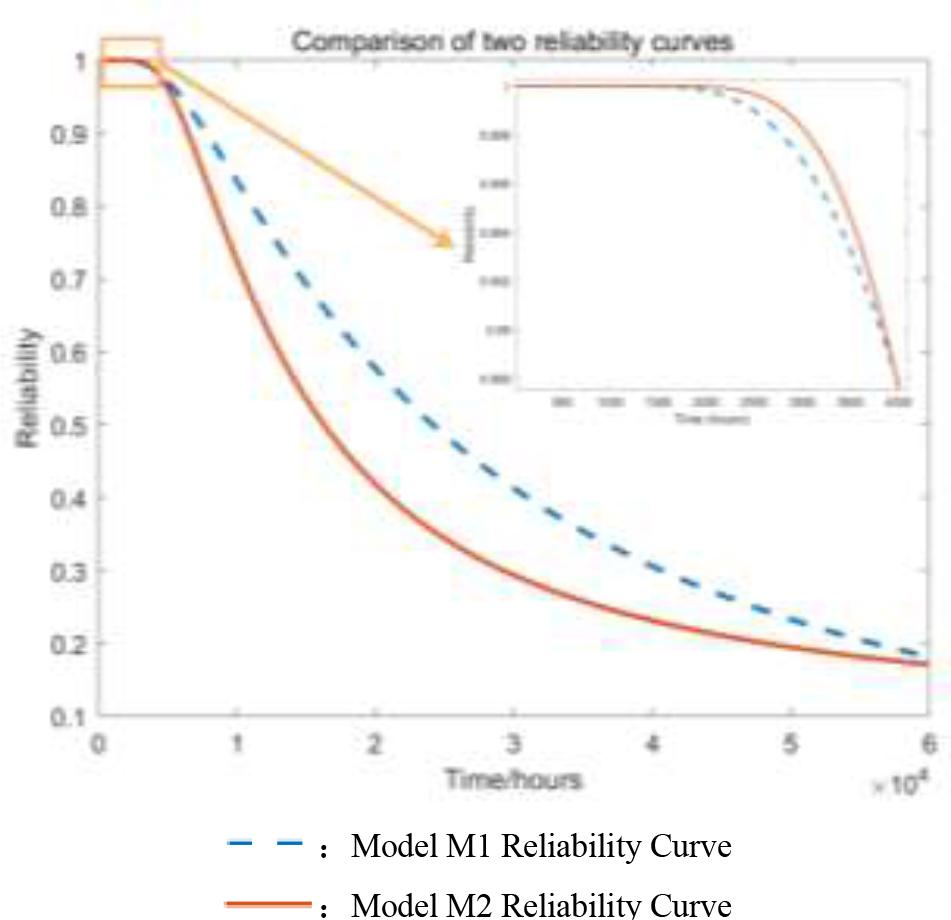
Model M1 vs. M2 Reliability Curve
As can be seen from Figure 8., if the zero-bias performance degradation trajectory of the fiberoptic gyroscopes in this batch is described by model M1, the reliability is lower than 1 from 1,704 h. In fact, none of the three gyroscopes tested failed by the 4032h test cutoff. In contrast, model M2 is more consistent with the reliability characteristics of fiber-optic gyroscopes with reliability below 1 from 2105 h. The model M1 is more consistent with the reliability characteristics of fiber-optic gyroscopes. Meanwhile, model M1 is more optimistic because the reliability curve declines more slowly without considering individual differences, whereas model M2 is more conservative but closer to the reality because the reliability declines more rapidly compared to M1 after the introduction of the consideration of individual differences and nonlinearities. Combined with the zero-bias failure threshold £0.1°/h), M2 is more suitable for longterm use scenarios, providing a more rigorous basis for equipment maintenance and avoiding potential risks caused by performance degradation.
In conclusion, the M2 model stands out as the most effective model, as it effectively accounts for both individual differences and nonlinear behaviors in the degradation process of fiber-optic gyroscopes.
In order to handle the individual variability and nonlinearity of performance degradation of fiberoptic gyros in reliability assessment, a method based on the nonlinear random effect Wiener process is proposed in this paper. The results show that the model can more accurately characterize the actual degradation behavior of the fiber optic gyro when considering the individual variability of the fiber optic gyro and the nonlinear characteristics of the performance degradation. In the validation of fiber-optic gyro zero-bias performance degradation data, the log-likelihood value of the proposed method is higher and the Akaike Information Criterion (AIC) value is lower than that of the model that only considers randomness, and the Q-Q plot exhibits characteristics that are closer to normal distribution, which proves the superior fitting ability of the model in interpreting the data. In conclusion, the model proposed in this paper can provide a more reasonable and accurate basis for the reliability assessment of fiber optic gyro and provides new theoretical support for the reliability analysis and performance optimization of inertial navigation equipment